Логарифмическая функция, ее свойства и график

Вопросы занятия:

·  рассмотреть свойства логарифмических функций, в зависимости от основания логарифма;

·  рассмотреть графики логарифмических функций, в зависимости от основания логарифма.

Материал урока

На прошлых уроках мы ввели понятие логарифма положительного числа по положительному и отличному от единицы основанию а.

Если для любого положительного числа можно найти логарифм по заданному основанию, то можно рассмотреть функцию вида:

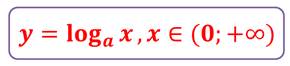
её график и свойства.

Давайте вспомним показательную функцию:

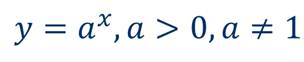
Эта функция монотонна, значит, она обратима.

Найдём для неё обратную функцию.

Значит, графики этих функций симметричны относительно прямой y = x.

Давайте попробуем построить график функции:

Составим таблицу некоторых значений функции. В качестве значений аргумента возьмём числа, являющиеся степенями числа два

Отметим полученные точки на координатной плоскости и соединим их плавной линией.

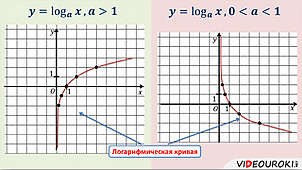
Получим логарифмическую кривую.

По графику нетрудно записать основные свойства функции. Поскольку такой же вид будут иметь графики функций:

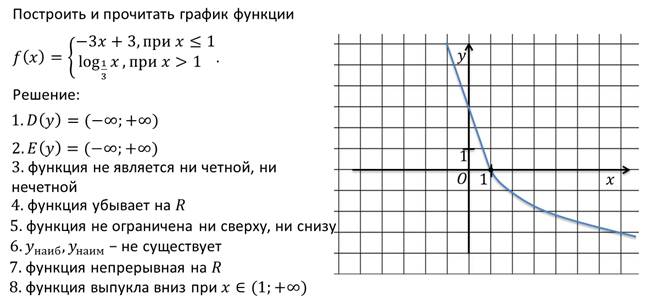
Итак, областью определения будет промежуток (0; + ∞).

Областью значений будет промежуток (– ∞; + ∞).

Функция не является ни чётной, ни нечётной.

Функция возрастает на всей области определения.

Функция не ограничена ни сверху, ни снизу.

Функция не имеет ни наибольшего, ни наименьшего значений.

Функция непрерывна на всей области определения.

Функция выпукла вверх на всей области определения.

Теперь давайте по точкам построим график функции:

Построим таблицу значений:

Отметим получившиеся точки на координатной плоскости и получим логарифмическую кривую.

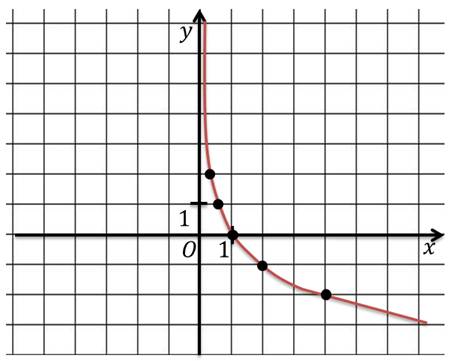
Запишем основные свойства функции:

Областью определения функции будет промежуток (0; + ∞).

Областью значений будет промежуток (– ∞; + ∞).

Функция не является ни чётной, ни нечётной.

Функция убывает на всей области определения.

Функция не ограничена ни сверху, ни снизу.

Функция не имеет ни наибольшего, ни наименьшего значений.

Функция непрерывна на всей области определения.

Функция выпукла вниз на всей области определения.

По графикам функций видно, что ось Oy вертикальная асимптота:

Рассмотрим несколько примеров.

Пример.

Пример.

Пример.

Пример.

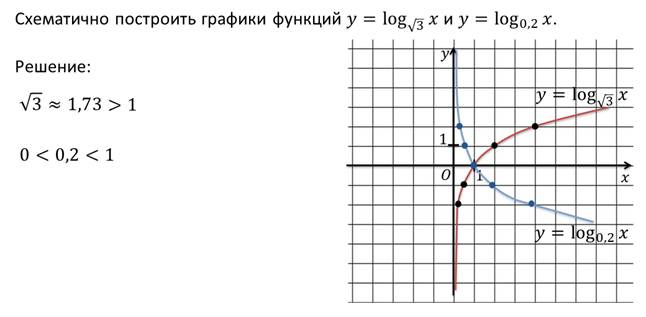
Пример.

Пример.

Итак, давайте ещё раз повторим, какие же функции называются логарифмическими и запишем их основные свойства: