Ранее вы уже сталкивались с координатами, но указывали их для точек. При этом работали в прямоугольной координатной плоскости, для задания которой необходимо было провести две взаимно перпендикулярные прямые с выбранными на них направлениями (их называют координатными осями) и выбрать единицу измерения на каждой из осей.
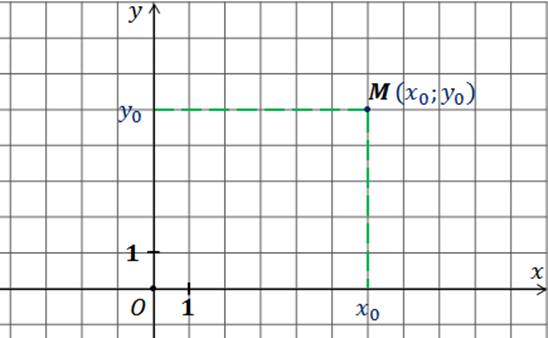
Это и позволяло определить координаты любой точки.
На этом уроке нам предстоит выяснить, что называют координатами вектора.
С прошлых занятий вам известно, что любой вектор на плоскости можно разложить по двум неколлинеарным векторам.
От
точки О начала координат отложим векторы  ,
длины которых равны единице (в дальнейшем будем называть такие векторы
единичными), так, чтобы направление вектора
,
длины которых равны единице (в дальнейшем будем называть такие векторы
единичными), так, чтобы направление вектора  совпадало с
направлением оси x, а направление вектора
совпадало с
направлением оси x, а направление вектора  совпадало
с направлением оси y.
совпадало
с направлением оси y.

Тогда
векторы  будем
называть координатными векторами. Понятно, что любой вектор
будем
называть координатными векторами. Понятно, что любой вектор  можно разложить по
векторам
можно разложить по
векторам  .
Причём коэффициенты разложения, числа x
и y, определяются единственным образом.
.
Причём коэффициенты разложения, числа x
и y, определяются единственным образом.
Так
вот коэффициенты разложения вектора  по координатным
векторам называют координатами вектора
по координатным
векторам называют координатами вектора  в данной системе
координат.
в данной системе
координат.
Координаты вектора будем записывать в фигурных скобках через точку с запятой. При этом первым будем записывать коэффициент разложения x, а вторым — y.
На
одном из прошлых занятий мы разлаживали векторы, изображённые в координатной
плоскости по векторам  .
.
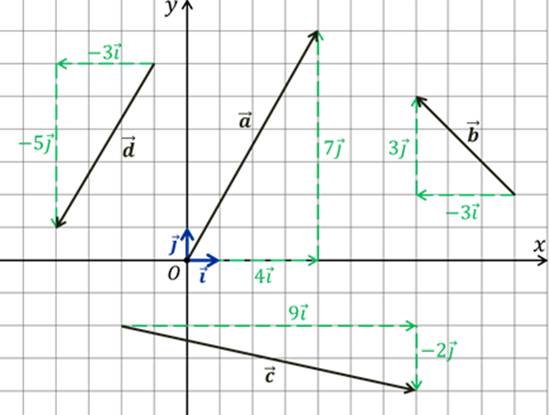
Пользуясь этими разложениями, запишем координаты данных векторов.
Итак,
вектор  имеет
координаты
имеет
координаты  .
.
Вектор  имеет
координаты
имеет
координаты  .
.
Координатами
вектора  являются
числа
являются
числа  ..
..
Ну,
а координатами вектора  будут
числа
будут
числа  .
.
Обратите
внимание, что такие координаты данные векторы будут иметь только в конкретной
системе координат и при конкретных координатных векторах  .
.
Коэффициенты
разложения нулевого вектора по векторам  равны
нулю. Тогда получаем, что нулевой вектор имеет координаты 0 0, причём в любой
системе координат и при любых координатных векторах.
равны
нулю. Тогда получаем, что нулевой вектор имеет координаты 0 0, причём в любой
системе координат и при любых координатных векторах.
Если
векторы равны, то их разложения по векторам  также
будут равны, а значит, равны будут и коэффициенты разложения. Таким образом,
получаем, что координаты равных векторов соответственно равны.
также
будут равны, а значит, равны будут и коэффициенты разложения. Таким образом,
получаем, что координаты равных векторов соответственно равны.
Рассмотрим ещё один особенный случай — противоположные векторы.
Их разложения противоположны. Значит, противоположны будут и соответственные координаты.
Можем подытожить, что координаты равных векторов соответственно равны, а координаты противоположных векторов соответственно противоположны.
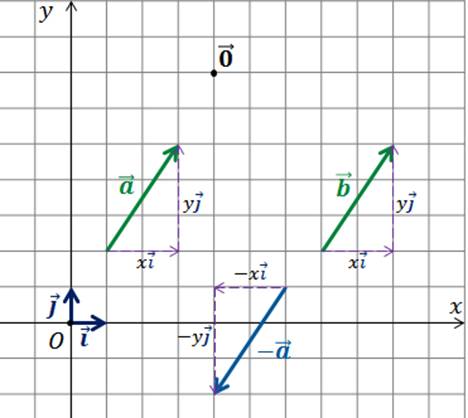
Пользуясь полученными выводами, для каждого из данных векторов запишем противоположный и укажем его координаты.
 ;
;  ;
;  ;
;  ;
;  .
.





Задача. Разложить векторы по
координатным векторам  и
и  , указать их координаты.
, указать их координаты.
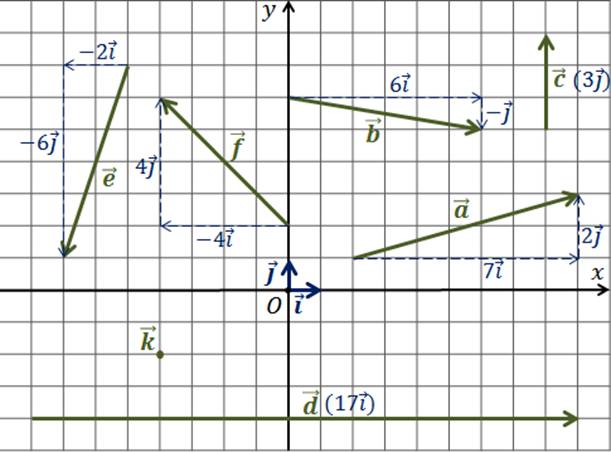
Начнём
с вектора  .
Его разложение
.
Его разложение  .
Значит, его координатами будут числа 7 и 2.
.
Значит, его координатами будут числа 7 и 2.
Далее
запишем разложение вектора  .
Коэффициенты разложения 6 и -1 являются его координатами.
.
Коэффициенты разложения 6 и -1 являются его координатами.
Вектор
 . Коэффициенты разложения
равны 0 и 3. Значит, вектор
. Коэффициенты разложения
равны 0 и 3. Значит, вектор  .
.
Следующим
рассмотрим вектор  .
Значит, координаты вектора
.
Значит, координаты вектора  .
.
Далее обратим своё внимание на вектор  . Тогда
координаты данного вектора
. Тогда
координаты данного вектора  .
.
Запишем разложение вектора  . Значит, он
имеет координаты
. Значит, он
имеет координаты  .
.
Последним рассмотрим вектор  . Тогда
получаем,
. Тогда
получаем,  .
.
Видим, что для определения координат вектора достаточно его
разложения по координатным векторам. Поэтому при наличии разложения вектора
можно сразу назвать его координаты. Главное — помнить, что в качестве первой
координаты записывают коэффициент разложения при координатном векторе,
коллинеарном оси x (в данном случае — это вектор  ), а в
качестве второй координаты — коэффициент разложения при координатном векторе,
коллинеарном оси y (в данном случае — это вектор
), а в
качестве второй координаты — коэффициент разложения при координатном векторе,
коллинеарном оси y (в данном случае — это вектор  ).
).
Запишем координаты векторов, пользуясь их разложениями по
координатным векторам  .
.
Из разложения вектора  видим, что он имеет координаты
видим, что он имеет координаты
 .
.
 , то
, то  ;
;
 , то
, то  ;
;
 , то
, то  ;
;
 , то
, то  .
.
А теперь, пользуясь только координатами данных векторов, построим их в прямоугольной координатной плоскости, откладывая каждый вектор от точки О начала координат.
Координатами
вектора  являются
числа 8 и -1. Значит, чтобы переместиться из точки О на вектор
являются
числа 8 и -1. Значит, чтобы переместиться из точки О на вектор  , сначала нужно
переместиться на вектор
, сначала нужно
переместиться на вектор  ,
а затем на вектор
,
а затем на вектор  .
Соединив точку О с конечной точкой, получим вектор
.
Соединив точку О с конечной точкой, получим вектор  .
.

Далее
изобразим вектор  .
Для этого из точки О переместимся на вектор
.
Для этого из точки О переместимся на вектор  .
Тем самым получим искомый вектор
.
Тем самым получим искомый вектор  .
.
Чтобы
из точки О переместиться на вектор  сначала
переместимся на вектор
сначала
переместимся на вектор  ,,
а затем на вектор
,,
а затем на вектор  .
Проведём вектор из точки О в конечную точку. Так мы получили вектор
.
Проведём вектор из точки О в конечную точку. Так мы получили вектор  .
.
Далее
построим вектор  .
.
Последним
построим вектор  .
Перемещение на этот вектор состоит из перемещений на вектор
.
Перемещение на этот вектор состоит из перемещений на вектор  и на вектор
и на вектор  . Перемещение из точки О
в конечную точку и задаёт вектор
. Перемещение из точки О
в конечную точку и задаёт вектор 
Так мы рассмотрели примеры построения вектора по его координатам.
Далее, пользуясь приобретёнными знаниями о координатах вектора, получим правила нахождения координат векторов, полученных уже известными вам действиями: сложением, вычитанием и умножением вектора на число.
Сначала
рассмотрим сумму двух векторов  ,
,  .
.
Пользуясь
их координатами, можем записать разложения данных векторов по координатным
векторам  ,
,  .
.
Сложим
полученные равенства  .
Пользуясь свойствами сложения векторов и произведения вектора на число,
получаем, что координаты вектора суммы векторов
.
Пользуясь свойствами сложения векторов и произведения вектора на число,
получаем, что координаты вектора суммы векторов  и
и  равны
равны  ,
,  .
.
Можем записать правило.
Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов.
Найдём
координаты векторов суммы, если вектор  ,
,
 ,
,  ,
,  .
.
Координаты
вектора суммы  и
и
 равны
равны  .
.
Координаты
вектора суммы  ,
,
 ,
,  равны
равны  .
.
Теперь
рассмотрим разность векторов  -
- .
.
Из
разложения вектора  вычтем
разложение вектора
вычтем
разложение вектора  .
.
Получаем,
что координаты вектора разности равны  .
.
Запишем правило. Каждая координата разности двух векторов равна разности соответствующих координат данных векторов.
Разность
векторов  и
и
 имеет координаты
имеет координаты  .
.
Разность
векторов  и
и
 имеет координаты
имеет координаты  .
.
Далее
получим координаты произведения вектора  на число k.
на число k.
Получаем,
что координаты произведения равны  .
.
Запишем правило. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Найдём
координаты вектора 4 .
Они равны
.
Они равны  .
.
Координаты
вектора 2,5  равны
равны
 .
.
Вектор
3  имеет координаты
имеет координаты  .
.
Ну,
а вектор 
 имеет
координаты
имеет
координаты  .
.
Все три правила, полученные нами, в дальнейшем помогут определять координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
Задача.
Найти
координаты векторов  и
и
 по координатам
данных векторов
по координатам
данных векторов  ,
,
 ,
,  ,
,  .
.


Представим это выражение в виде суммы.
Вектор
 имеет координаты
имеет координаты  , или
, или  .
.
Вектор
 имеет
координаты
имеет
координаты  ,
или
,
или  .
.
Координаты
вектора  . А вот координаты
вектора
. А вот координаты
вектора  .
.
Координаты
вектора  найдём
как суммы соответствующих координат полученных векторов. В результате получаем,
что
найдём
как суммы соответствующих координат полученных векторов. В результате получаем,
что  имеет
координаты
имеет
координаты 
Далее
найдём координаты вектора  .
Запишем второй множитель в виде суммы. Координаты векторов
.
Запишем второй множитель в виде суммы. Координаты векторов  и
и  . Вектор
. Вектор  имеет координаты
имеет координаты  , или
, или  . Вектор
. Вектор  .
.
Сумма
полученных векторов будет иметь координаты  .
.
Произведение
этого вектора на 3 имеет координаты  .
Это и есть координаты вектора
.
Это и есть координаты вектора  .
.
Подведём итоги урока. Сегодня, пользуясь уже известным правилом разложения вектора по двум неколлинеарным векторам, мы ввели понятие координатных векторов и дали определение координатам вектора. А также получили правила нахождения координат векторов суммы векторов, разности векторов и произведения вектора на число. Этих правила позволяют определять координаты векторов, представленных в виде алгебраической суммы данных векторов с известными координатами.
На следующем уроке мы найдём связь между координатами вектора и координатами его начала и конца.

 Получите свидетельство
Получите свидетельство Вход
Вход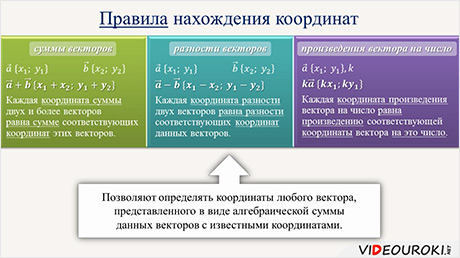



 2
2 13904
13904



Здравствуйте, Александра. Пока не планируем.
Здравствуйте. Подскажите, пожалуйста, планируете ли вы конспекты включать в проект в текстовой варианте и pdf?