Вам уже хорошо знакомо понятие вектора, и вы умеете выполнять некоторые действия над векторами. А именно: складывать, вычитать и умножать вектор на число.
На этом уроке мы приступаем к более глубокому изучению вопроса о векторах и для начала запишем лемму о коллинеарных векторах.
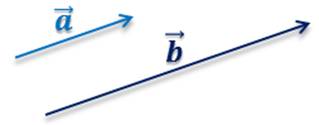
Лемма. Если
векторы 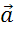 и
и
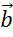 коллинеарны
и
коллинеарны
и 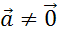 ,
то существует такое число
,
то существует такое число 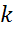 ,
что
,
что 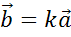 .
.
Доказательство.
1. 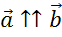
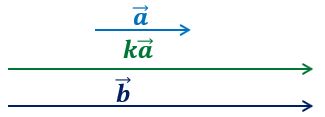
Пусть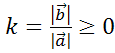 ,
тогда
,
тогда 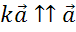 .
.
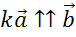
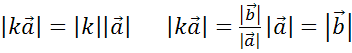
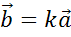
2. 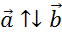
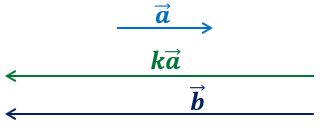
Пусть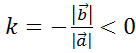 ,
тогда
,
тогда 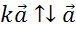 .
.
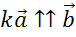
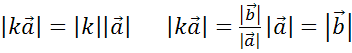
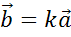
Что и требовалось доказать.
Выполним задание.
Выразить
коллинеарные векторы 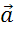 ,
,
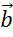 ,
,
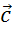 ,
,
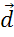 ,
,
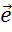 и
и
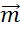 через
коллинеарный им вектор
через
коллинеарный им вектор 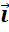 .
.
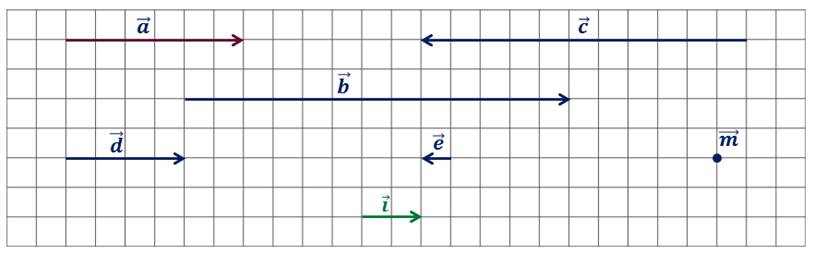
Решение.
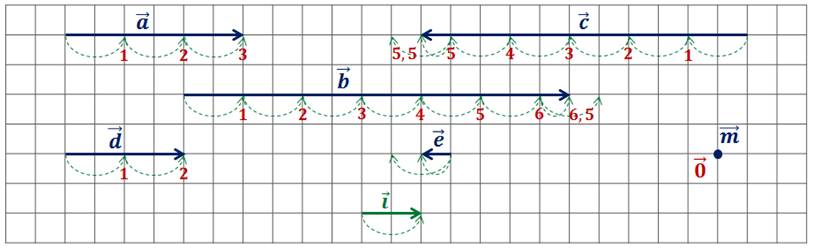
Итак,
начнём с вектора 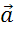 Видим,
что векторы
Видим,
что векторы 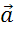 и
и
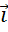 сонаправлены.
Значит, k>0.
сонаправлены.
Значит, k>0.
Также,
взяв длину вектора 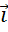 за
единицу, видим что длина вектора
за
единицу, видим что длина вектора 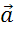 в
3 раза больше.
в
3 раза больше.
Можем
записать, что вектор 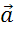 равен
произведению вектора
равен
произведению вектора 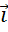 на
число 3.
на
число 3.
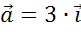
Рассмотрим
следующий вектор, вектор 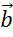 .
Он так же сонаправлен с вектором
.
Он так же сонаправлен с вектором 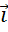 ,
поэтому k>0. При этом длина
вектора
,
поэтому k>0. При этом длина
вектора 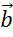 в
6,5 раза больше длины вектора
в
6,5 раза больше длины вектора 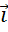 .
.
Тогда
вектор 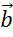 равен
произведению вектора
равен
произведению вектора 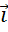 на
6,5.
на
6,5.
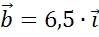
Далее
рассмотрим вектор 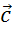 .
.
Он противоположно
направлен с вектором 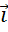 .
Поэтому k<0. К тому же длина
вектора
.
Поэтому k<0. К тому же длина
вектора 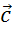 в
5,5 раза больше длины вектора
в
5,5 раза больше длины вектора 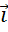 .
Тогда вектор
.
Тогда вектор 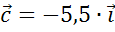 .
.
Далее
не сложно записать, что вектор 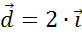 .
.
Следующим рассмотрим вектор
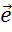 .
Он противоположно направлен вектору
.
Он противоположно направлен вектору 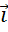 и
его длина в 2 раза меньше, поэтому вектор
и
его длина в 2 раза меньше, поэтому вектор 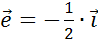 .
.
Остался вектор 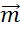 .
Как видите, он нулевой. Нам известно, что нулевой вектор сонаправлен любому
вектору. И его длина равна нулю. Поэтому вектор
.
Как видите, он нулевой. Нам известно, что нулевой вектор сонаправлен любому
вектору. И его длина равна нулю. Поэтому вектор 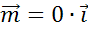 .
.
Сейчас вспомним правило параллелограмма сложения двух векторов.
Если векторы-слагаемые 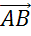 и
и
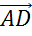 отложены
от одной точки, то, построив на них параллелограмм ABCD,
мы получим вектор
отложены
от одной точки, то, построив на них параллелограмм ABCD,
мы получим вектор 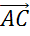 их
суммы.
их
суммы.
Обозначим
вектор 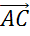 как
вектор
как
вектор 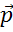 .
Он равен сумме
.
Он равен сумме 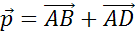 .
.
В
свою очередь вектор 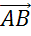 всегда
можно выразить как произведение коллинеарного ему вектора
всегда
можно выразить как произведение коллинеарного ему вектора 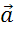 на
некоторое число x, а вектор
на
некоторое число x, а вектор 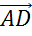 —
как произведение коллинеарного ему вектора
—
как произведение коллинеарного ему вектора 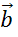 на
некоторое число y.
на
некоторое число y.
Тогда
можно записать, что вектор 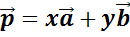 .
.
В
таком случае говорят, что Вектор 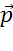 разложен по неколлинеарным векторам
разложен по неколлинеарным векторам 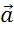 и
и 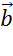 .
. 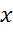 ,
, 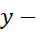 коэффициенты разложения.
коэффициенты разложения.
Теорема. На плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.
Доказательство.
Пусть данными векторами
будут неколлинеарные векторы 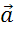 и
и
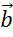 .
.
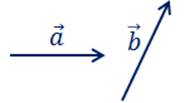
Докажем, что любой вектор
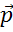 можно
разложить по данным векторам.
можно
разложить по данным векторам.
1.
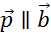
В
этом случае по лемме о двух коллинеарных векторах получаем, что вектор
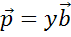 .
.
Так
же можно записать его разложение по векторам 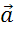 и
и
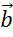 .
Только коэффициент разложения при векторе
.
Только коэффициент разложения при векторе 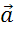 будет
равен нулю
будет
равен нулю 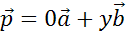 .
.
2. 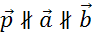
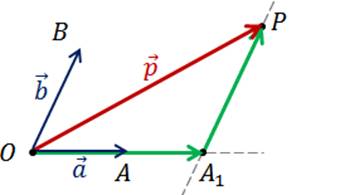
Отметим
некоторую точку О и отложим от неё векторы 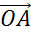 ,
,
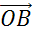 и
и
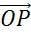 ,
равные векторам
,
равные векторам 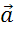 ,
,
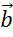 и
и
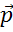 соответственно.
соответственно.
Через
точку P проведём прямую
параллельную прямой 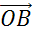 .
Точку пересечения полученной прямой с ОА обозначим как А1.
.
Точку пересечения полученной прямой с ОА обозначим как А1.
По
правилу треугольника вектор 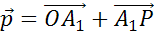 .
Вектор
.
Вектор 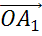 коллинеарен
вектору
коллинеарен
вектору 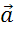 ,
вектор
,
вектор 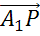 коллинеарен
вектору
коллинеарен
вектору 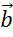 .
Это значит, что вектор
.
Это значит, что вектор 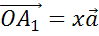 ,
а вектор
,
а вектор 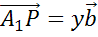 .
.
Отсюда
получаем, что вектор 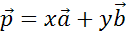 .
Тем самым мы разложили его по векторам
.
Тем самым мы разложили его по векторам 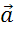 и
и
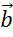 .
.
Первая часть теоремы доказана. Действительно, на плоскости любой вектор можно разложить по двум данным неколлинеарным векторам.
Теперь докажем, что коэффициенты разложения x и y определяются единственным способом.
Допустим,
что кроме разложения 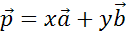 возможно
другое разложение,
возможно
другое разложение, 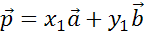 .
.
Вычтем второе равенство из первого.
Получаем,
что нулевой вектор можно разложить по векторам 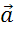 и
и
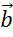 ,
при этом коэффициенты разложения равны
,
при этом коэффициенты разложения равны 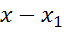 и
и
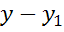 .
.
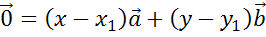 .
.
Такое
возможно только в том случае, если данные коэффициенты разложения равны нулю. А
значит, при 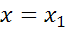 и
и
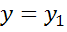 .
.
Значит, коэффициенты разложения определяются единственным способом.
Что и требовалось доказать.
Рассмотрим
пример. Запишем разложение вектора 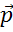 по
векторам
по
векторам 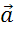 и
и
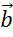 .
.
Все
они отложены от точки О. При этом векторы 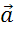 ,
,
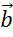 и
и
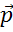 равны
векторам
равны
векторам 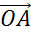 ,
,
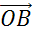 и
и
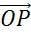 соответственно.
соответственно.
Через точку P проведём прямую, параллельную OB. И точку пересечения этой прямой с ОА назовём А1.
По
правилу треугольника вектор 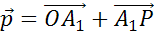 .
Вектор
.
Вектор 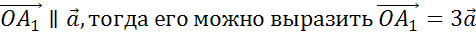 .
.
Аналогично,
выразим 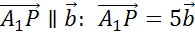 .
.
Тогда
разложение вектора 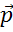 по
векторам
по
векторам 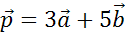
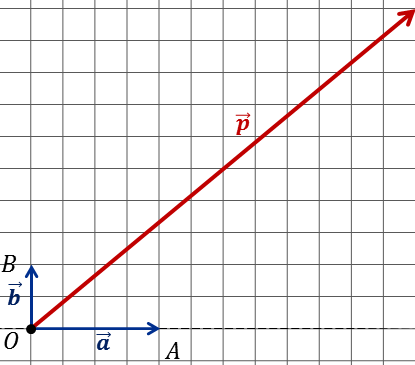
Теперь
выполним задание, в котором векторы 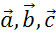 и
и
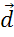 ,
изображённые в координатной плоскости, нужно разложить по двум векторам
,
изображённые в координатной плоскости, нужно разложить по двум векторам 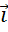 и
и
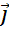 .
.
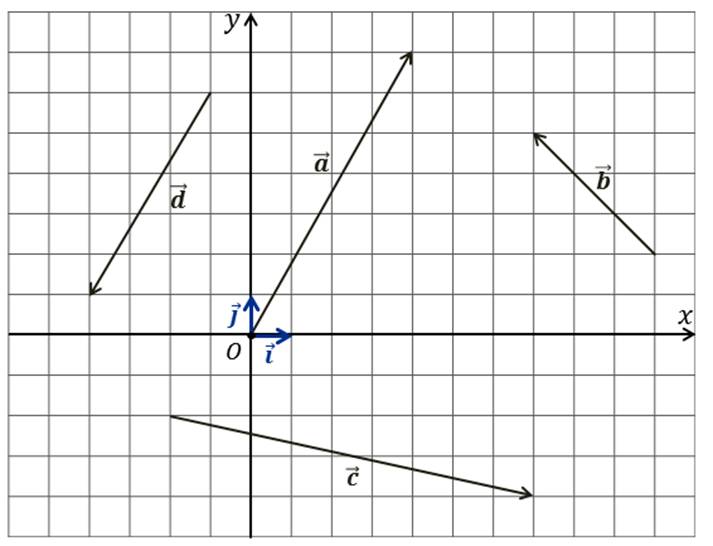
Итак,
начнём с вектора 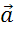 .
Восстановим для него правило треугольника сложения двух векторов так, чтобы
вектор
.
Восстановим для него правило треугольника сложения двух векторов так, чтобы
вектор 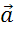 являлся
вектором суммы, а векторы-слагаемые
являлся
вектором суммы, а векторы-слагаемые 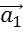 и
и
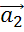 были
коллинеарны векторам
были
коллинеарны векторам 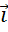 и
и
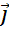 соответственно.
соответственно.
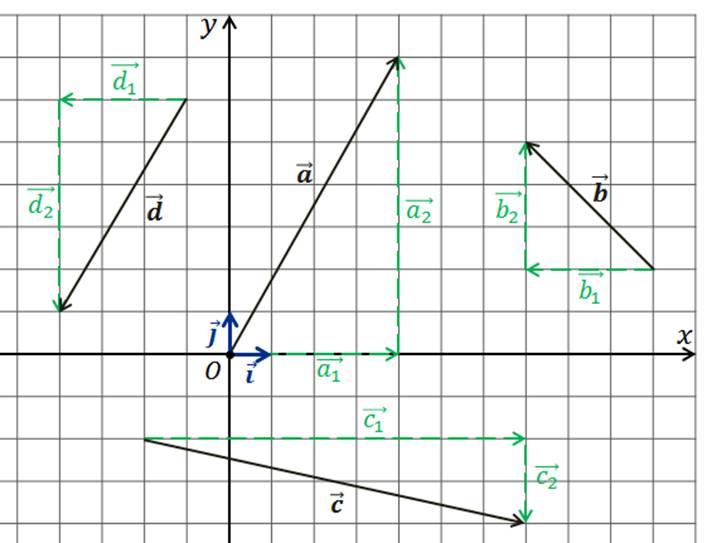
Аналогично поступим с другими векторами.
На примере этого задания вы увидели, как можно раскладывать векторы по двум неколлинеарным векторам.
Подведём итоги урока.
Сегодня вы узнали, что любой вектор можно выразить через коллинеарный ему вектор умножением на некоторое число k.
Также мы рассмотрели примеры и убедились в том, что на плоскости любой вектор можно разложить по двум данным неколлинеарным векторам, причём коэффициенты разложения определяются единственным образом.

 Получите свидетельство
Получите свидетельство Вход
Вход




 9
9 50661
50661


Здравствуйте, Олеся. Обновите страницу, нажав ctrl+F5.
Нет, не исправили. Я сделала скриншот данной страницы. В конспекте, который находится под видеоуроком ошибка не исправлена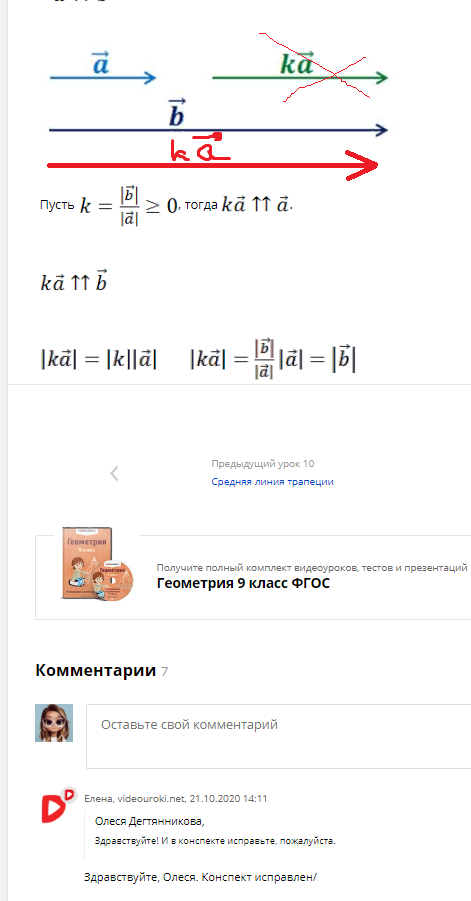
Здравствуйте, Олеся. Конспект исправлен/
Здравствуйте, Олеся.
Благодарим Вас за внимание к нашему проекту. Материал будет проверен.
Здравствуйте! И в конспекте исправьте, пожалуйста.
Здравствуйте, Олеся.
Спасибо за Ваш комментарий. Действительно в уроке вектор нарисован некорректно. Урок исправили.
Здравствуйте, Олеся.
Благодарим Вас за внимание к нашему проекту. Материал будет проверен.
Ошибка! На рисунке векторы коллинеарны. В случае неколлинеарных векторов аналогичная ошибка.