Определение:
Дробным рациональным уравнением называется уравнение, обе части которого являются рациональными выражениями, причём хотя бы одно из них - дробным выражением.
Алгоритм решения:
· найти общий знаменатель дробей, входящих в уравнение;
· умножить обе части уравнения на общий знаменатель;
· решить получившееся целое уравнение;
· исключить из корней те, которые обращают общий знаменатель в ноль.
Пример.
Решить уравнение:
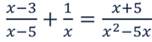
Знаменатель дроби, стоящей в правой части уравнения, можно разложить на множители, тогда найдем общий знаменатель:
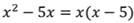
Умножим на него обе части уравнения, получим уравнение:
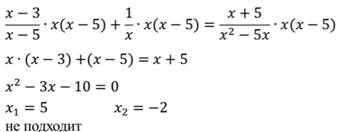
Проверим, x=5 обращает общий знаменатель в ноль, а x=-2 знаменатель не обращает в ноль, значит x=-2 является корнем данного дробного рационального уравнения.
Получили корень x=-2.
Пример.
Решить уравнение:
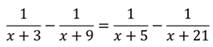
Найдём область допустимых значений переменной:
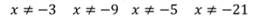
Приведём к общему знаменателю дроби:
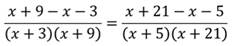
Получим целое уравнение:
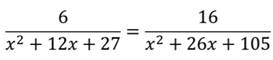
Преобразовав его, получаем квадратное уравнение:
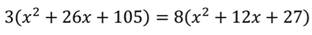
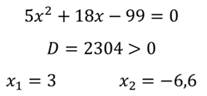
Так как корни не входят в область допустимых значений, значит оба числа являются корнями исходного дробного рационального уравнения.
Пример.
Решить уравнение:
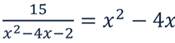
Введем замену:
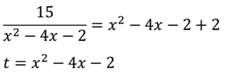
Решаем по алгоритму:
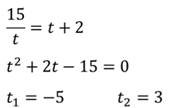
Осуществим обратную подстановку и решим полученные квадратные уравнения:
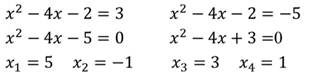
Проверим найденные корни:
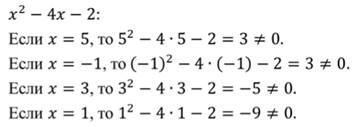
Ни при каком из полученных значений знаменатель не обращается в ноль. Значит, данное дробное рациональное уравнение имеет 4 корня.
Больших вычислений требует проверка. Каждый корень нужно подставлять в уравнение.
Пример.
От автобусной остановки отъехал автобус до аэропорта, находящегося на расстоянии 120 км. Один из пассажиров автобуса опоздал к отправлению на 10 минут, и решил поехать на такси. Автобус и такси приехали в аэропорт одновременно. Нужно найти скорость автобуса, если известно, что скорость такси на 10 км/ч больше.
Пусть х - скорость автобуса, тогда (х + 10) - скорость такси. Выразим время движения обоих транспортных средств и составим уравнение:
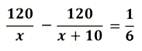
Решим полученное дробное рациональное уравнение:
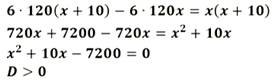
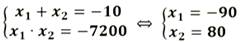
Получаем скорость автобуса 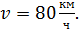

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 17139
17139