Решение неравенств второй степени с одной переменной

Неравенства вида:

где х - переменная,

a, b, c - некоторые числа.

В левой части неравенства записан квадратный трёхчлен. Решение неравенства сводится к нахождению множества значений переменной х, при которых квадратный трёхчлен принимает положительные или отрицательные значения.

Алгоритм решения неравенств второй степени:

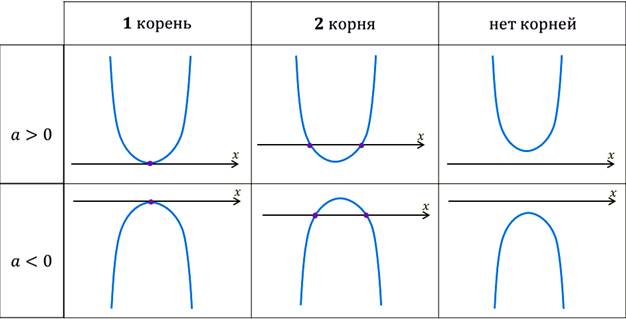
1.     Определить направление ветвей параболы .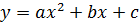

2.     Найти корни квадратного уравнения .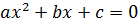

3.     Изобразить схематический график.

4.     Выбрать множество значений х, соответствующих знаку неравенства.

5.     Записать ответ.

Решим несколько неравенств второй степени, придерживаясь данного алгоритма.

Первое неравенство:

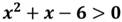
Рассмотрим квадратичную функцию:

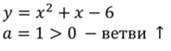
Так как а=1, значит ветви параболы направлены вверх.

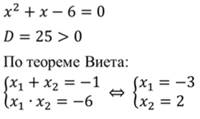
Отметим эти значения на оси:

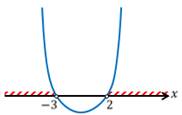
Решением данного неравенства будет объединение промежутков:

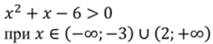
Второе неравенство:

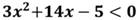
Рассмотрим квадратичную функцию:

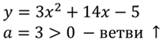
Так как а=3, значит ветви параболы направлены вверх.

Решим соответствующее квадратное уравнение:

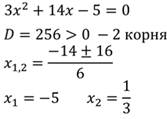
Отметим эти значения:

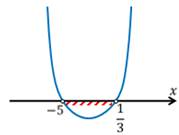
Решением данного неравенства будет:

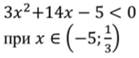
Третье неравенство:

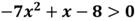
Рассмотрим квадратичную функцию:

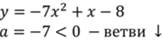
Так как а=-7, значит ветви параболы направлены вниз.

Решим соответствующее квадратное уравнение:

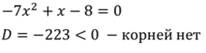
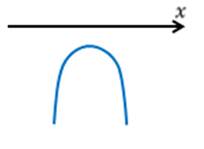
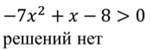
Данное неравенство не имеет решений.

Пример.

Определить, при каком значении переменной b уравнение имеет корни:

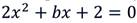
Найдем дискриминант этого уравнения:

Тогда выполнение задания сводиться к решению неравенства второй степени. Причём с нестрогим знаком, больше либо равно.

Применив алгоритм, найдем корни уравнения:

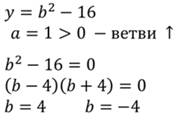
Изобразим их на числовой прямой:

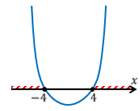
Уравнение имеет корни:

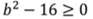
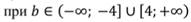
Пример.

Решить систему неравенств:

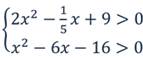
Решим каждое неравенство в отдельности.

В первом случае:

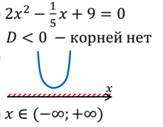
Во втором случае:

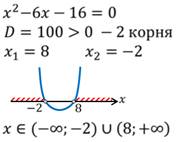
Мы получили решение двух неравенств второй степени. Вернёмся к системе. Решением системы будет пересечение двух решений. Значит, решением системы будет объединение промежутков: