Целое уравнение и его корни

Определение:

Целым уравнением с одной переменной называется уравнение, левая и правая части которого - целые выражения.

Отличие целого уравнения от дробно-рационального заключается в том, что областью определения целого уравнения является множество всех действительных чисел. То есть аргумент может принимать любые значения.

Среди уравнений найдем те, которые являются целыми уравнениями с одной переменной.

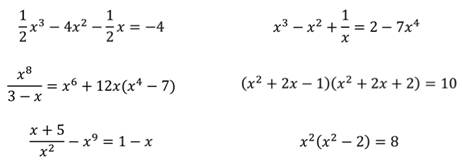
Целыми будут следующие уравнения.

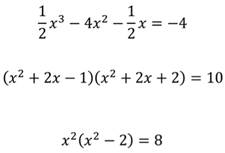
Каждое из этих уравнений можно преобразовать.

Первое уравнение:

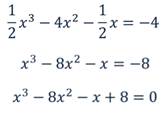
Во втором уравнении:

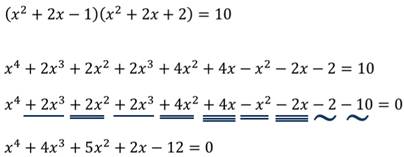
В третьем уравнении:

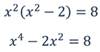
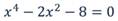
Определение:

Степень многочлена P(x) называют степенью уравнения P(x)=0.

Степень первого уравнения  P(x)=3, степень второго уравнения P(x)=4, степень третьего уравнения P(x)=4.

Рассмотрим пример: определить степень уравнений.

1.                 

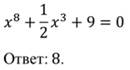
2.                  

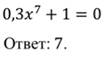
3.                 

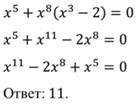
4.                   

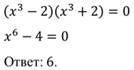
Любое уравнение 1 - й степени можно привести к виду  - это линейное уравнение, и оно имеет не более одного корня.

Уравнение 2 - й степени можно привести к виду  - это квадратное уравнение и оно имеет не более двух корней.

Уравнение 3 - й степени можно записать в виде , оно имеет не более трёх корней.

Уравнения 4 - й степени можно представить в виде , оно имеет не более четырёх корней.

Любое целое уравнение n - й степени можно представить в таком виде , оно имеет не более n корней.

Причём, во всех этих случаях, a≠0.

Пример.

Решить уравнение:

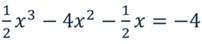
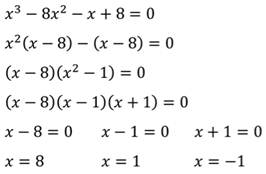
Данное уравнение имеет три корня.

Рассмотрим пример: решить уравнение.

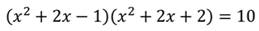
Так как для него трудно найти способ решения, будем работать с исходной записью. Введём замену.

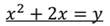
Получим новое уравнение, решим его:

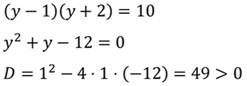
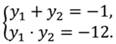
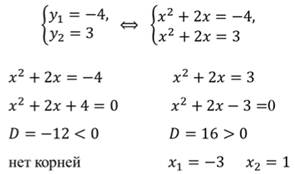
При решении этого уравнения мы применили способ введения новой переменной. С помощью этого способа легко решать уравнения вида . Такие уравнения имеют специальное название - «биквадратные уравнения».

Алгоритм решения биквадратного уравнения:

1.                Ввести новую переменную .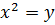

2.                Решить уравнение 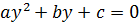, полученное после подстановки новой переменной.

3.                Выполняю обратную подстановку .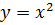

4.                Найти корни исходного биквадратного уравнения.

Пример.

Решить уравнение:

Приведем его к биквадратному уравнению:

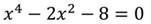
Введём новую переменную и выполним подстановку: