Вероятности событий

Вероятности событий принято обозначать большой буквой  латинского алфавита по первой букве слова probabilitas, которое в переводе с латинского языка означает «вероятность». Например, вероятность события  обозначают .

Правило вычисления вероятностей.

Вероятность события равна сумме вероятностей элементарных событий, благоприятствующих этому событию.

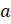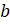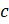Пусть событию  благоприятствуют элементарные события , ,  и .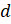

Вероятность события  равна сумме вероятностей этих элементарных событий.

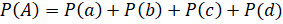
Число элементарных событий, благоприятствующих данному событию, а, следовательно, и число слагаемых в правой части равенства может быть каким угодно и даже бесконечным.

Напомним, что вероятности элементарных событий назначают, следуя двум правилам.

Первое правило. Вероятности элементарных событий неотрицательны.

Второе правило. Сумма вероятностей всех элементарных событий равна 1.

Получается, что вероятность события  неотрицательна и не превосходит 1, то есть справедливо двойное неравенство.

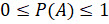
В частности, вероятность невозможного события равна 0, а вероятность достоверного события – 1.

Достоверным является событие, которому благоприятствуют все элементарные события случайного эксперимента.

Пример. В шахматной партии Саша играет с Лёшей. Вероятность выигрыша Саши равна 0,4, вероятность ничьей равна 0,2, вероятность того, что партия не будет закончена, равна 0,1. Давайте найдём вероятность того, что Саша не проиграет.

Пусть событие  – «Саша не проиграет».

Этому событию благоприятствуют 3 элементарных события: «Саша выиграет»… «будет ничья», «партия не будет закончена».

Вероятность события  равна сумме вероятностей этих элементарных событий.

Известно, что вероятность того, что Саша выиграет, равна 0,4, вероятность ничьей равна 0,2, а вероятность того, что партия не будет закончена, равна 0,1. Тогда получается, что вероятность события , то есть того, что Саша не проиграет, равна 0,7.

Найдём вероятность того, что Лёша не проиграет.

Пусть событие  – «Лёша не проиграет».

Лёша не проиграет, если Саша не выиграет. А значит, вероятность события  найдём, отняв от 1 вероятность того, что Саша выиграет. Выполним вычитание и получим, что вероятность события , то есть того, что Лёша не проиграет, равна 0,6.

Найдём вероятность того, что никто не выиграет.

Пусть событие 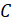 – «никто не выиграет».

Никто не выиграет, если будет ничья или партия не будет закончена. Следовательно, вероятность события 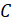 равна сумме этих элементарных событий, то есть равна 0,3.

Пример. В городской школе выбрали наугад 100 учеников и попросили замерить, сколько минут каждый из них тратит на дорогу в школу.

Получили результаты.

Эти результаты сгруппировали в таблице. Шаг группировки – 8 мин.

Это можно рассмотреть как случайный эксперимент, в котором 7 элементарных событий. В качестве вероятности каждого элементарного события будем брать частоту соответствующего интервала.

Если значение попадает на границу двух интервалов, то его можно отнести к любому из них. В этом примере мы будем относить граничное значение к правому интервалу.

Найдём вероятность того, что школьники тратят на дорогу меньше, чем 35 мин.

Пусть событие  – «школьники тратят на дорогу меньше, чем 35 мин».

Элементарные события, принадлежащие этому событию, выделим в таблице зелёным цветом.

Вероятность события  равна сумме вероятностей этих элементарных событий.

Найдём вероятность того, что школьники тратят на дорогу больше, чем 50 мин.

Пусть событие  – «школьники тратят на дорогу больше, чем 50 мин».

Этому событию принадлежит только одно элементарное событие. Оно выделено в таблице синим цветом.

Следовательно, вероятность события  равна вероятности этого элементарного события, то есть равна 0,09.

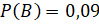
Выполним несколько заданий.

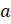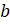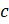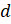Задание первое. В случайном эксперименте четыре элементарных события: , ,  и , вероятности которых соответственно равны 0,2, 0,3, 0,4 и 0,1. Найдите вероятность события, которому благоприятствуют элементарные события.

Решение. Из условия известно, что , , .

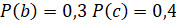Задание второе. На тарелке лежат одинаковые на вид пирожки: 5 с мясом, 7 с капустой и 8 с картошкой. Костя наугад берёт один пирожок. Какова вероятность того, что пирожок окажется с мясом?

Решение.

Задание третье. Симметричную монету бросают 2 раза. Найдите вероятность того, что орёл выпадет хотя бы 1 раз.

Решение.

До встречи на следующих занятиях!