Понятие функции

Вопросы занятия:

·  ввести понятия «функциональная зависимость»;

·  узнать о способах задания функции;

·  познакомиться с историей функции.

Материал урока

Изучение темы начнём с рассмотрения нескольких примеров.

Пример.

В рассмотренном примере переменную t называют независимой переменной, так как её значения мы выбирали произвольно. А переменную s называют зависимой переменной, так как её значения определяются выбранными значениями переменной t.

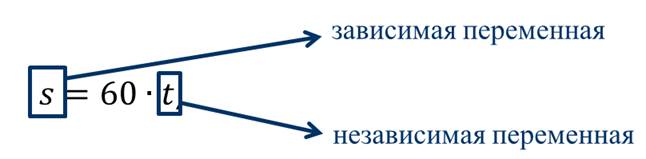
Давайте рассмотрим ещё один пример.

Пример.

В этом примере переменная а является независимой переменной, а переменная Р – зависимой переменной.

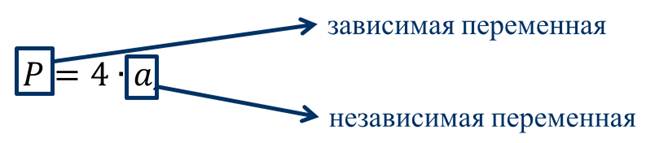
В рассмотренных примерах каждому значению независимой переменной соответствует единственное значение зависимой переменной. Такую зависимость одной переменной от другой называю функциональной зависимостью или функцией.

Независимую переменную называют также аргументом, а зависимую – функцией от этого аргумента.

Так в рассмотренных примерах путь, пройденный автомобилем, является функцией от времени движения автомобиля. А периметр квадрата является функцией от его стороны.

Определение.

Значения, которые принимает независимая переменная, образуют область определения функции.

Определение.

Все значения зависимой переменной называют значениями функции.

А сейчас выполним следующее упражнение.

В семнадцатом веке французские математики Рене Декарт и Пьер Ферма впервые начали выражать зависимость между переменными при помощи формулы.

В рассмотренных выше примерах функции задавались с помощью формулы. И этот способ задания функции является более распространённым. Но давайте рассмотрим ещё несколько примеров.

На рисунке показано, как изменялась высота гиацинта в зависимости от его возраста. Рост указан в сантиметрах, а его возраст в днях.

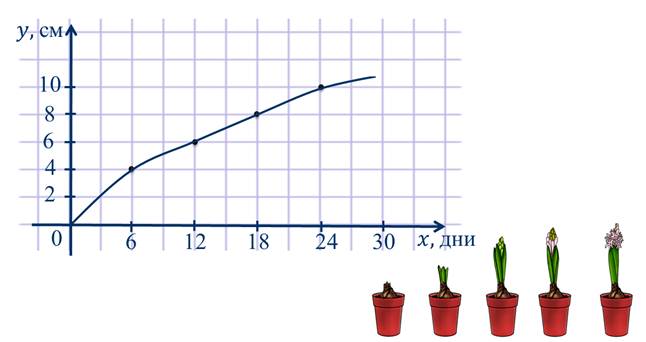
С помощью этого графика мы можем сказать, какую высоту имеет цветок в зависимости от его возраста. Например,

В данном случае икс является независимой переменной, а игрек – зависимой переменной.

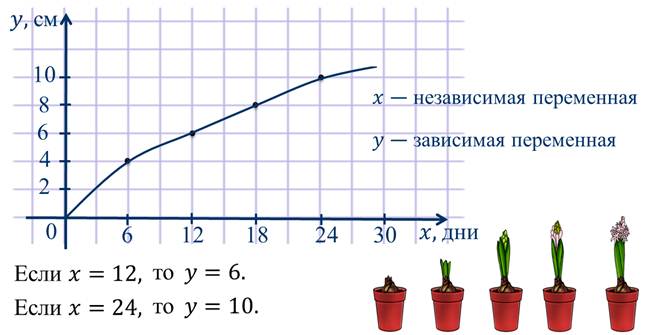
Здесь зависимость одной переменной от другой также является функциональной зависимостью, или функцией. Но, в отличие от предыдущих примеров, функция задана в виде графика.

И рассмотрим таблицу, в которой представлен результат измерений средней температуры воздуха в комнате в течение недели.

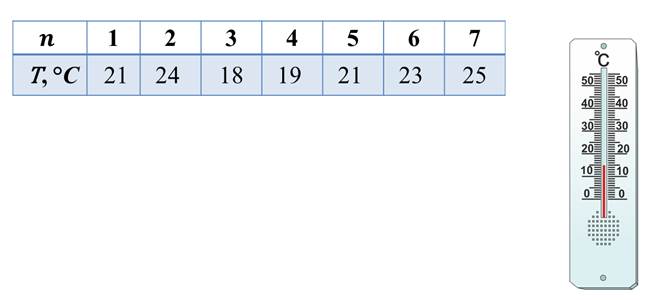
В данной таблице каждому значению n (то есть номеру дня недели) соответствует значение t (температуры воздуха в комнате). Например,

Здесь каждому значению независимой переменной соответствует единственное значение зависимой переменной.

А такую зависимость мы называем функцией. В этом примере функция задана в виде таблицы.