Прежде чем приступить к рассмотрению новой темы, напомним, что испытанием Бернулли, или просто испытанием называют случайный опыт, который может закончиться одним из двух элементарных событий: успехом или неудачей.
Вероятность того, что испытание Бернулли закончится успехом, принято
обозначать буквой  , а вероятность неудачи – буквой
, а вероятность неудачи – буквой  .
.
Вероятность успеха и вероятность неудачи в сумме дают 1. А значит, вероятность неудачи можно найти как разность 1 и вероятности успеха.


Чтобы в испытании было действительно два возможных события,
считают, что  и
и  .
.
Вероятность элементарного события  , в котором перед успехом случилось ровно
, в котором перед успехом случилось ровно  неудач, равна
неудач, равна  .
.
Также напомним, что последовательность одинаковых независимых испытаний, каждое из которых может окончиться либо успехом, либо неудачей называют серией испытаний Бернулли.
Элементарным событием в серии испытаний Бернулли является не отдельный успех или неудача, а последовательность успехов и неудач.
В серии из  испытании Бернулли всего
испытании Бернулли всего  различных элементарных событий.
различных элементарных событий.
В серии из  испытаний Бернулли вероятность элементарного события, в котором
произвольным образом чередуются
испытаний Бернулли вероятность элементарного события, в котором
произвольным образом чередуются  успехов и
успехов и  неудач, равна
неудач, равна  .
.
Сколько элементарных событий в серии из  испытаний Бернулли благоприятствуют наступлению определённого
числа успехов?
испытаний Бернулли благоприятствуют наступлению определённого
числа успехов?
Пример. Пусть проводится 6 испытаний. Сколько элементарных событий в этой серии благоприятствуют событию «случится ровно 5 успехов»?
Применим обозначения: У для успеха, Н для неудачи.
Элементарные события серии из 6 испытаний с 5 успехами выглядят так: УУУУУН, УУУУНУ, УУУНУУ, УУНУУУ, УНУУУУ, НУУУУУ.
Обратите внимание, что элементарных событий с 5 успехами в 6
испытаниях ровно столько, сколько способов расставить 5 букв У в
последовательности из 6 букв. Это равно  .
.
Действительно, получилось 6 элементарных событий.
Обобщим полученный результат на произвольное число испытаний  .
.
Число элементарных событий, благоприятствующих  успехам в серии из
успехам в серии из  испытаний, равно
испытаний, равно  .
.
Задача. Чтобы быстрее считать мелочь и давать сдачу, кассир в метро заранее складывает монеты столбиками по 10 монет в каждом. При этом кассир кладёт монеты случайной стороной вверх. Выясним, сколько всего есть способов положить 10 монет в столбик так, чтобы ровно 7 из них лежали орлом вверх.
В этом случайном опыте положение каждой монеты внутри столбика можно считать испытанием Бернулли с успехом «монета орлом вверх». Выкладывание столбика – серия из 10 испытаний. Число требуемых успехов равно 7.
В таком случае вопрос задачи можно сформулировать так: сколько элементарных событий благоприятствуют наступлению 7 успехов в 10 независимых испытаниях Бернулли?
Чтобы ответить на этот вопрос, найдём  .
.

 можно было найти и с помощью треугольника Паскаля. Напомним, что
столбцы и строки треугольника Паскаля нумеруются начиная с 0.
можно было найти и с помощью треугольника Паскаля. Напомним, что
столбцы и строки треугольника Паскаля нумеруются начиная с 0.

Выполним задания.
Задание первое. Выпишите все элементарные события, которые благоприятствуют: а) 1 успеху в серии из 4 испытаний Бернулли; б) 3 успехам в серии из 5 испытаний Бернулли.
Решение.


Задание второе. Сколько элементарных событий в серии из 6 испытаний Бернулли благоприятствует: а) 2 успехам; б) 4 успехам.
Решение.


Задание третье. Проведена серия из  испытаний Бернулли. Найдите
испытаний Бернулли. Найдите  Н, если общее число элементарных событий равно: а) 32; б) 128.
Н, если общее число элементарных событий равно: а) 32; б) 128.
Решение.

Задание четвёртое. Докажите, что в серии из 12 испытаний Бернулли число элементарных событий, благоприятствующих 4 успехам, равно числу элементарных событий, благоприятствующих 8 неудачам.
Решение.

До встречи на наших занятиях!

 Получите свидетельство
Получите свидетельство Вход
Вход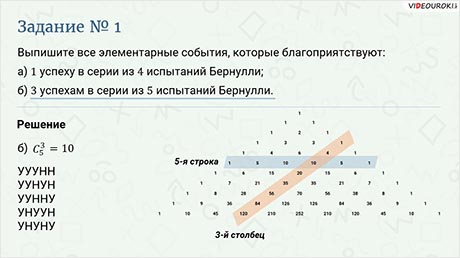




 668
668