Серия испытаний Бернулли

Прежде чем приступить к рассмотрению новой темы, напомним, что испытанием Бернулли, или просто испытанием, называют случайный опыт, который может закончиться одним из двух элементарных событий: успехом или неудачей.

Вероятность того, что испытание Бернулли закончится успехом, обычно обозначают буквой , а вероятность неудачи – буквой .

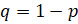
Чтобы в испытании было действительно два возможных события, считают, что  и .

Вероятность элементарного события , в котором перед успехом случилось ровно  неудач, равна .

Примером испытания Бернулли является подброшенная монета, которая может упасть либо орлом, либо решкой вверх.

Часто испытания проводятся снова и снова до наступления первого успеха. Например, монету подбрасывают до тех пор, пока не выпадет орёл.

Случайный опыт. Испытания проводят заданное количество раз, независимо от того, успехом или неудачей окончилось предыдущее.

Важно, чтобы одинаковые испытания можно было проводить много раз и чтобы они были независимыми, то есть исход каждого не должен быть связан с предыдущим.

Отметим, что такую серию испытаний можно устроить далеко не всегда. Ведь бывают испытания, которые повторить не удаётся. Например, краш-тест – испытание автомобиля на безопасность при столкновении. Если манекен, который сидит внутри автомобиля, не получил серьёзных повреждений, то тест считают успешным. Однако надёжность выводов при краш-тесте не очень высокая, так как автомобиль разбивается, а значит, повторить испытание в тех же условиях не получится. Конечно, можно использовать другие такие же автомобили, но делать множество автомобилей для того, чтобы их разбить, слишком дорого. Поэтому для производителей автомобилей, железнодорожной техники, самолётов очень важно собирать информацию об отказах и авариях, которые произошли уже в процессе эксплуатации.

Если удаётся провести определённое количество одинаковых и независимых испытаний подряд, то говорят, что проведена серия испытаний Бернулли.

Серия испытаний Бернулли – это последовательность одинаковых независимых испытаний, каждое из которых может окончиться либо успехом, либо неудачей.

Рассмотрим последовательность из трёх испытаний. Каждое испытание может окончиться либо успехом (У), либо неудачей (Н).

Составим таблицу элементарных событий и их вероятностей.

Отдельные испытания Бернулли независимы, поэтому вероятность каждого элементарного события можно найти с помощью правила умножения вероятностей.

Обратите внимание, что для  испытаний мы получили , то есть  элементарных событий. Для  испытаний будет , то есть  элементарных событий. Для  испытаний будет , то есть  элементарных события и т. д. Тогда получается, что для  испытаний будет  элементарных событий.

Элементарным событием в серии испытаний Бернулли является не отдельный успех или неудача, а последовательность успехов и неудач.

В серии из  испытаний Бернулли всего  различных элементарных событий.

Пример. Бросание симметричной монеты представляет собой простейшую серию испытаний Бернулли.

В этом опыте вероятность успеха (то есть вероятность выпадения орла) и вероятность неудачи (то есть вероятность выпадения решки) одинаковы и равны . Поэтому вероятности всех элементарных событий одинаковы.

Если монету бросают  раза, то вероятность каждого из  элементарных событий будет равна . А вот если монету бросают  раз, то всего будет  элементарных события, вероятность каждого из которых равна .

В этом примере мы рассмотрели серию испытаний, где вероятности успеха и неудачи одинаковы.

Пример. Биатлонист делает по очереди 5 выстрелов по 5 мишеням. Известно, что он попадает по мишеням в среднем 7 раз из 10. Какова вероятность того, что будут поражены вторая, третья и пятая мишени, а первая и четвёртая – нет?

Обратите внимание, что в биатлоне мишени окрашены в чёрный цвет. Поражённые мишени закрываются белыми щитками.

Успехом будем считать попадание в мишень, а неудачей – промах.

Событие, вероятность которого нам надо найти, в наших обозначениях имеет вид НУУНУ.

В условии сказано, что биатлонист попадает в мишень в среднем 7 раз из 10. А значит, вероятность успеха . Тогда вероятность неудачи .

В этом примере мы рассмотрели серию испытаний, где вероятности успеха и неудачи не одинаковы.

Запомните! В серии из  испытаний Бернулли вероятность элементарного события, в котором произвольным образом чередуются  успехов и  неудач, равна .

Выполним несколько заданий.

Задание первое. Эксперимент состоит из четырёх последовательных испытаний Бернулли. Пользуясь обозначениями У для успеха и Н для неудачи, выпишите все элементарные события, в которых: а) ровно 2 успеха; б) ровно 3 успеха.

Отметим, что в рассматриваемой серии из четырёх испытаний Бернулли всего  элементарных событий.

Решение.

Задание второе. Игральный кубик бросают 3 раза. Найдите вероятность события, которое состоит в том, что 6 очков выпадет: а) только при первом броске; б) только при втором и третьем бросках.

Решение.

Задание третье. Стрелок в тире стреляет по мишени. Вероятность попадания при каждом отдельном выстреле равна 0,6. Найдите вероятность того, что, сделав 5 выстрелов, стрелок попадёт в мишень только при первом и пятом выстрелах.

Решение.

До встречи на наших занятиях!