Сегодня мы с вами познакомимся с таким разделом математики как алгебра логики. Также узнаем, что такое логические переменные и логические значения.
Для начала узнаем, что же такое алгебра. Алгебра – это раздел математики, который изучает уравнения, содержащие цифры и буквенные обозначения, представляющие величины, подлежащие определению.
Например, x + y = 6.. Это алгебраическое уравнение, которое содержит переменные x и y. Если одна из переменных будет известна, можно будет найти вторую. Само же слово «алгебра» происходит от арабского Al-jabr, что означает «найти неизвестное». Многое из того, что изучает алгебра, вы проходите в школе на уроках математики. Например, натуральные, целые и рациональные числа, многочлены, множества и многое другое.

То есть вы знакомитесь с такими разделами математики, как алгебра чисел, алгебра множеств и так далее.
Существует ещё и такой раздел математики как алгебра логики. Для информатики это очень важный раздел. Алгебра логики – это раздел математической логики, который изучает высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними. То есть в этом разделе математики подразумевается только два значения – истинно или ложно.
Высказывание – это предложение на любом языке, содержание которого можно однозначно определить, как истинное или ложное.
Давайте разберёмся на примере некоторых предложений.
«Москва – столица России».
«Шесть минус два равно четыре».
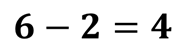
По поводу этих предложений можно сказать с уверенностью, что они истинны.
А вот, например, предложение «Зайцы зимой впадают в спячку.» – ложно.


Все вышеперечисленные предложения являются высказываниями, так как можно однозначно сказать истинны они или ложны.
В естественных языках высказывания выражаются с помощью повествовательных предложений, но стоит помнить, что не все повествовательные предложения являются высказываниями. Например, предложение «Если попасть камнем в окно, то оно разобьётся.» не является высказыванием, так как нельзя однозначно сказать истинно оно или ложно.

Ведь в нём не уточняется какой камнем будет бросаться, маленький или большой, и с какой силой.
Или ещё одно предложение «Физическая культура – самый важный школьный предмет.» так же не относится к высказываниям, потому что для кого-то это важный предмет, так как ученик собирается дальше идти учится, например, на тренера, и соответственно для него это высказывание будет истинным. А вот для ученика, который планирует учиться на программиста, это высказывание будет ложным.


Но в тоже время предложение «Физкультура является очень полезным уроком.» будет являться истинным высказыванием, так как действительно, развитие интеллекта без физического здоровья будет неполноценный – так же, как и в обратном случае
Также стоит запомнить, что высказываниями не являются побудительные и вопросительные предложения. Например, «Сколько времени?», «Чей телефон звонит на уроке?», «Сколько тебя можно ждать!».
Для построения высказываний могут использоваться знаки различных формальных языков: математики, физики, химии и других.
Например, предложение
«Гипотенуза прямоугольного треугольника находится по следующей формуле ![]() .»
является высказыванием, так как оно истинно.
.»
является высказыванием, так как оно истинно.

Или же ещё одно «Формула воды в химии записывается так: H2O.» также является высказыванием.

«Путь при равномерном
прямолинейном движении находится по формуле ![]() ».
».

Это предложение является высказыванием,
но высказыванием ложным, так как формула для нахождения пути при равномерном
прямолинейном движении выглядит следующим образом: ![]() .
.
Числовые выражения не являются высказываниями. Но, в то же время, если из двух выражений составить одно и соединить их знаком равенства или неравенства, то новое выражение будет высказыванием. К примерам можно отнести следующие выражения:
![]()
![]()
Первое выражение истинно, так как 10 умноженное на 5 равно 50 и 43 плюс 7 также равно 50, соответственно они равны.
А вот второе ложно, так как 23, умноженное на 6, равно 138. Число 138 в свою очередь больше 100, а у нас стоит знак меньше.
Равенства или неравенства, которые содержат в себе переменные, также не относятся к высказываниям. Примерам будет являться неравенство x + y < 7. Но если переменные заменить цифрами, например, 3 + 5 < 7, то такое неравенство становится высказыванием, так как мы заменили переменные конкретными значениями.
Рассмотрим ещё несколько неравенств:
![]()
![]()
![]()
Первое и второе неравенства являются ложными, так как 5 + 2 = 7. А у нас знак больше. Восемь равно восьми, но никак не меньше.
А вот третье является верным, так как 8 < 9.
Истинно или ложно то или иное высказывание, мы решаем, исходя из тех наук, к которым оно относится. Например, когда мы с вами рассматривали неравенства, мы обращались к науке «Математика».
Важным же фактором для алгебры логики является не содержание высказываний, а истинно или ложно то или иное высказывание. В алгебре логики высказывания обозначаются при помощи букв. Такие обозначения называются логическими переменными.
Например, нам даны два высказывания:
![]()
![]()
Первое обозначим буквой А, латинского алфавита, а второе – буквой В.
Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей, а если ложно – нулём.
Вернёмся к нашим высказываниям А и В. Первое высказывание истинно, значит его логическая переменная А будет равна 1, а вот второе выражение ложно, значит В будет равно 0.
А = 1.
В = 0.
0 и 1, которые обозначают значения логических переменных, называются логическими значениями.
Таким образом алгебра логики определяет правила записи, упрощения и преобразования высказываний и вычисления их значений.
Производя операции с логическими переменными, которые могут быть равны только 0 или 1, с помощью алгебры логики можно свести обработку информации к операциям с двоичными данными.
В основе всех компьютерных устройств, с помощью которых происходит хранение и обработка информации, лежит аппарат алгебры логики.
С применением элементов алгебры логики вы столкнётесь и во многих других разделах информатики.
А теперь пришла пора подвести итоги нашего урока.
Сегодня мы узнали, что:
· Алгебра логики – это раздел математической логики, который изучает высказывания, рассматриваемые со стороны их логических значений (истинности или ложности), и логические операции над ними.
· Высказывание – это предложение на любом языке, содержание которого можно однозначно определить, как истинное или ложное.
· Логические переменные – это высказывания, которые обозначаются в алгебре логики при помощи букв.
· Логические значения – это цифры ноль и один, которые обозначают значения логических переменных.

 Получите свидетельство
Получите свидетельство Вход
Вход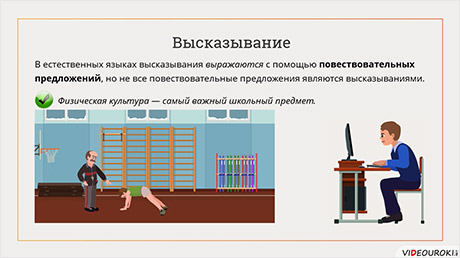




 10941
10941

