Представление чисел в компьютере

На данном уроке мы с вами узнаем, как представляются целые и вещественные числа в компьютере.

А начнём мы с вами с целых чисел.

Как вы уже знаете, целые числа – это множество чисел, которое состоит из натуральных чисел, чисел, противоположных натуральным, и нуля.

Итак, оперативная память представляет собой таблицу, то есть состоит из ячеек.

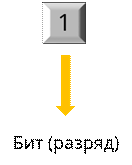
Каждая ячейка оперативной памяти представляет собой физическую систему, которая состоит из некоторого числа однородных элементов. Эти элементы обладают двумя устойчивыми состояниями, которые соответствуют двум числам – нулю и единице. Каждый такой элемент предназначен для хранения одного из битов – разряда двоичного числа. Поэтому каждый элемент ячейки называется битом или разрядом.

То есть, можно сказать, что каждая ячейка оперативной памяти содержит число, представленное в двоичной системе счисления, так как вся информация представлена в памяти компьютера именно в этой системе счисления. Каждая ячейка также включает в себя некоторое количество клеточек (ячеек). В каждой клеточке содержится число ноль или один. Это зависит от того, какой код соответствует изначальному числу.

Давайте рассмотрим одну ячейку, которая состоит из n разрядов.

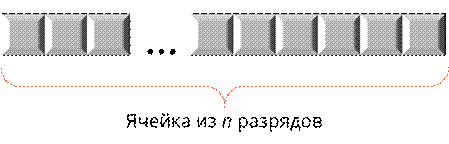
Она разбита на n клеточек. n обозначает количество разрядов или битов, отведённых под исходное число. Первая клеточка слева – это (n-1)-й разряд. Вторая – (n-2)-й разряд и так далее. Последняя клеточка – это 0-й разряд.

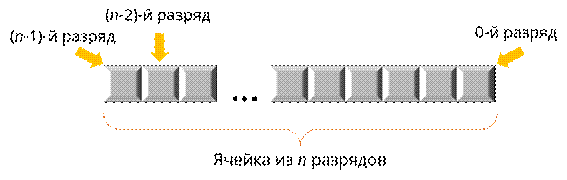
Можно сказать, что разряд – это степени для числа два в двоичной системе счисления.

Для представления целых чисел в компьютере существует несколько различных способов, которые отличаются друг от друга количеством разрядов и наличием или отсутствием знакового разряда. Обычно под целые числа отводится 8, 16, 32 или 64 разряда или бита.

Существует беззнаковое и знаковое представление чисел. Беззнаковое представление можно использовать только для неотрицательных чисел, отрицательные же числа представляются только в знаковом виде.

Беззнаковое представление используется для таких объектов, как адреса ячеек; счётчиков, например, количество символов в тексте; чисел, которые обозначают дату и время; размеров графических изображений в пикселях и много другое.

Для этих данных используется беззнаковое представление, так как они никак не могут быть отрицательными числами.

Давайте рассмотрим таблицу максимальных значений для беззнаковых целых n -разрядных чисел:

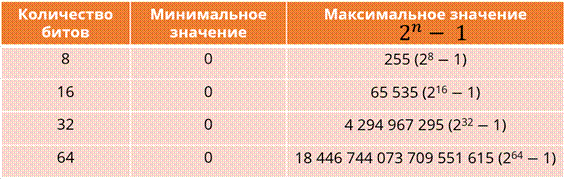
В первом столбце указано количество битов, во втором минимальное значение, а в третьем – максимальное значение.

Минимальное значение во всех строка равно нулю. А вот максимальное вычисляется по формуле 2ⁿ – 1. То есть максимальное восьмиразрядное число будет равно 255.

2⁸ – 1 = 256 – 1 = 255.

Максимальное значение целого неотрицательного числа достигается в том случае, когда во всех разрядах ячейки хранятся единицы.

Давайте разберёмся на примере.

Возьмём восьмиразрядную ячейку и поместим в неё максимально допустимое число 255.

Исходя из этого можем сказать, что наша ячейка состоит из 8 разрядов или клеточек. При переводе числа 255 в двоичную систему счисления получим 8 единиц. То есть в каждой клеточке будет содержаться по единице.

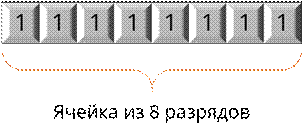
Число разрядов n=8. Давайте над каждой клеточкой расставим соответствующий разряд начиная с крайней левой.

n – 1 = 8 – 1 = 7.

n – 2 = 8 – 2 = 6.

n – 3 = 8 – 3 = 5.

n – 4 = 8 – 4 = 4.

n – 5 = 8 – 5 = 3.

n – 6 = 8 – 6 = 2.

n – 7 = 8 – 7 = 1.

n – 8 = 8 – 8 = 0.

Давайте вспомним общий вид нашей ячейки.

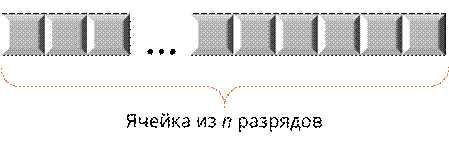
То есть ячейка из n разрядов, в нашем случае 8, состоит из n клеточек (снова из 8), а каждый разряд вычисляется по формуле n – 1, n – 2 и так далее. В зависимости от того, на каком месте находится ячейка.

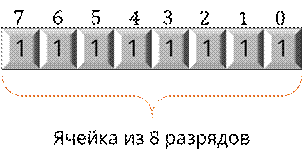
А если мы возьмём все наши единицы и проставим над ними наши разряды, то мы можем перевести наше число из двоичной системы счисления в десятичную уже известным нам образом.

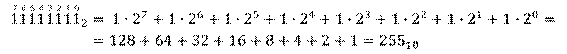
Если же брать число 256, то мы не сможем поместить его в восьмиразрядную ячейку, так как оно будет состоять из единицы и восьми нулей, а клеточек у нас 8.

Если мы возьмём число 65 535, то в двоичной системе счисления оно будет состоять из 16 единиц. А если шестнадцатиразрядную ячейку снова представить, как строку, состоящую из 16 клеточек и расставить соответствующие разряды, то она будет выглядеть следующим образом:

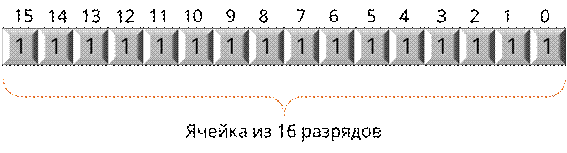
Для получения компьютерного представления беззнакового целого числа достаточно перевести его в двоичную систему счисления и дополнить полученный результат слева нулями до стандартной разрядности.

Давайте рассмотрим, как будет выглядеть число 125 в восьмиразрядном и шестнадцатиразрядном представлениях. Для этого переведём наше число в двоичную систему и получим следующее:

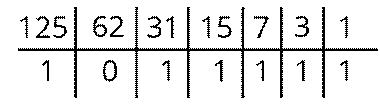
125₁₀ = 1111101₂.

Наше число состоит из 7 цифр. Поместим его в восьмиразрядную ячейку.

Но ячеек 8, а цифр 7. В таком случае помещаем наше число в крайние справа семь ячеек, а в первую левую запишем ноль.

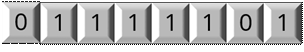
Он не повлияет на наше число, но все разряды ячейки должны быть заполнены цифрами.

А если мы поместим это же число в шестнадцатиразрядную ячейку, то получим 9 ячеек слева, заполненных нулями, а в остальных 7 будет располагаться наше число.

То есть можно сказать, что мы записываем наше число в двоичной системе счисления, а затем дополняем эту двоичную запись незначащими нулями слева в зависимости от того, из скольких разрядов состоит наше представление числа.

Это то, что касается беззнакового представления чисел.

При представлении числа со знаком (плюсом, если это положительное число, и минусом, если это отрицательное число) самый старший разряд, то есть тот, который находится слева, отводится под знак числа, а остальные разряды – под само число. Если число положительное, то в самый старший разряд (самую левую клеточку) пишется цифра 0, а если отрицательное, то 1.

Такое представление чисел называется прямым кодом. Такие коды в компьютере используются для хранения положительных чисел в запоминающих устройствах, для выполнения операций с положительными числами.

Например, число 56 в двоичной системе будет равно: 111000₂.

Оно в себя включает 6 цифр. Запишем его в восьмиразрядную ячейку.

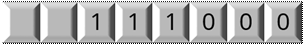
Две оставшиеся слева клеточки заполним нулями, так как число положительное.

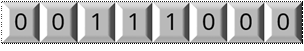
А если бы наше число было отрицательным, то оно выглядело бы следующим образом.

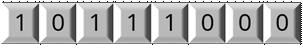
В старший разряд мы поставили единицу, так как число отрицательное.

Для выполнения операций с отрицательными числами используется дополнительный код, который позволяет заменить операцию вычитания сложением.

Дополнительный код целого отрицательного числа может быть получен по следующему алгоритму:

·                   записать прямой код модуля числа;

·                   инвертировать его (заменить единицы нулями, нули – единицами);

·                   прибавить к инверсному коду единицу.

Давайте рассмотрим применение этого алгоритма на примере.

Нам дано число –25. При переводе в двоичную систему модуля числа получим следующее число: 11001₂.

Теперь смотрим на первый пункт. Нам необходимо записать прямой код модуля числа. Возьмём восьмиразрядный код. То есть наше число будет записано в клеточки, а в трёх пустых клеточках слева от него – нули.

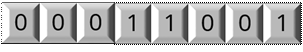
Далее во втором пункте нам необходимо инвертировать наше число, то есть заменить единицы нулями, а нули – единицами. Получим следующее:

Теперь нам осталось, исходя из третьего пункта, прибавить к числу единицу. Получим следующее число:

Всё, что говорилось ранее, относилось к представлению целых чисел. Для представления вещественных чисел используется немного другой способ. Давайте рассмотрим его.

Любое вещественное число A может быть записано в экспоненциальной форме:

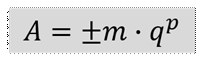
m – мантисса числа.

q – основание системы счисления.

p – порядок числа.

Возьмём для примера число 1 345 572. Его можно представить различными способами:

С экспоненциальной формой записи вы наверняка уже встречались. Например, считая на калькуляторе, вы могли получить следующее число: 1,34Е + 6.

Оно обозначает следующее: 1,34 · 10⁶. То есть знак Е – это основание десятичной системы счисления.

Из примера, можно сделать вывод, что положение запятой может изменяться.

Для единообразия мантиссу обычно записывают как правильную дробь, которая имеет после запятой цифру, отличную от нуля. То есть наше число 1 345 572 будет выглядеть следующим образом: 1 345 572 = 0,1345572 • 10⁷.

Вещественное число может занимать в памяти компьютера 32 или 64 разряда.

То есть наша ячейка в памяти может состоять из 32 или 64 клеточек. При этом выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы.

Давайте разберёмся на примере. Возьмём число 125 в десятичной системе счисления и запишем её в тридцатидвухразрядную ячейку.

Для начала нам нужно перевести число 125 в двоичную систему счисления. Получим следующее: 125₁₀ = 1111101₂.

Теперь запишем это число в экспоненциальной форме.

Ставим равно. Мантиссой числа будет следующее: 0,1111101.

1111101₂ = 0,1111101

Ставим знак умножения. q – это основание системы счисления. В нашем случает это двоичная система счисления. Число 2 в двоичной системе счисления будет состоять из цифр 1 и 0. Запишем его.

1111101₂ = 0,1111101 · 10.

p – это порядок числа или же степень. Мы с вами перенесли наше число на семь знаков вправо после запятой. Значит наше p будет равно 7. При переводе числа семь в двоичную систему счисления получим следующее:

7₁₀ = 111₂.

1111101₂ = 0,1111101 · 10¹¹¹.

Мы с вами записали двоичное число в экспоненциальной форме.

Теперь перенесём всё в клеточки ячейки памяти, размером 32 разряда.

Под знак и порядок выделяется восемь клеточек, под знак и мантиссу двадцать четыре.

Первую клеточку слева выделяем под знак. Так как наше число положительное, то ставим цифру 0.

В разделе «Знак и порядок» запишем число 7 в двоичной системе счисления. Оставшиеся клеточки заполним нулями.

Теперь переходим к разделу «Знак и мантисса». В первой слева снова ставим цифру ноль, которая обозначает, что знак нашего числа положительный.

Далее запишем наше число, а оставшиеся клеточки заполним нулями.

Мы записали наше число в тридцатидвухразрядную ячейку.

Диапазон представления вещественных чисел определяется количеством разрядов, отведённых для хранения порядка чисел, а точность – количеством разрядов, отведённых для хранения мантиссы.

Давайте рассмотрим следующий пример:

В нём максимальное значение порядка числа составляет: 1111111₂ = 127₁₀.

Следовательно, максимальное значение числа будет равно: 0,11111111111111111111111 · 10¹¹¹.

Широкий диапазон представления вещественных чисел важен для решения научных и инженерных задач. Но в тоже время алгоритмы обработки таких чисел более трудоёмки по сравнению с алгоритмами обработки целых чисел.

А теперь пришла пора подвести итоги урока.

Сегодня мы узнали, как представляются целые и вещественные числа в компьютере, а также научились преобразовывать числа в ячейки памяти, учитывая разрядность ячейки.