Для начала вспомним, что такое двоичная система.
Итак, двоичная система счисления – это позиционная система счисления с основанием два. Алфавит двоичной системы счисления: 0 и 1.
На прошлом уроке мы с вами познакомились с восьмеричной и шестнадцатеричной системами счисления и научились переводить из восьмеричной и шестнадцатеричной систем счисления в десятичную и наоборот.
Сегодня на уроке мы научимся производить арифметические действия в двоичной системе счисления, познакомимся с «компьютерными» системами счисления, а также узнаем, как происходит обмен информацией между компьютерами.
Давайте познакомимся с двоичной арифметикой.
Вся арифметика двоичной системы счисления основывается на использовании двух таблиц сложения и умножения. Давайте рассмотрим их.


Для начала научимся слаживать двоичные числа.

Как вы можете видеть первая строка и первый столбец заполнены числами 0 и 1. При сложении всё очень просто.
0 + 0 = 0.
1 +0 = 1.
А вот 1 плюс 1 будет равно числу, состоящему из 1 и 0.
Давайте попробуем сложить два числа: 101002 и 11012. Сложение в столбик такое же, как и в десятичной системе сложения. Запишем наши числа в столбик для сложения.

Начинаем с конца.
0 + 1 = 1.

0 + 0 = 0. Запишем это число.

1 + 1 = 10.
0 пишем под чертой, а 1 запоминаем.

0 + 1 = 1.
Но у нас есть ещё 1, которую мы запомнили, то есть 0 + 1 + 1 = 10. Пишем внизу 0, а 1 запоминаем.

1 + 1 = 10.

Мы с вами произвели сложение двоичных чисел.
А теперь давайте проверим, правильно ли мы всё сделали. Для этого переведём числа, которые нам даны изначально, в десятичную систему. Итак, запишем первое число и проставим степени для двойки справа налево.

Ставим равно и записываем следующее:

Для подсчёта вспомним из математики степени двойки.

Получим:

Числа, которые умножаются на ноль, мы не записывали, так как в результате мы всё равно получаем ноль.
Запишем второе число в двоичной системе счисления и также расставим степени для двойки справа налево.

Ставим равно и записываем следующее:

Ставим равно и сосчитаем:

Необходимо помнить, что любое число в нулевой степени равно единице.
Теперь сложим два числа в десятичной системе счисления.
2010 + 1310 = 3310.
Переведём число 33 в двоичную систему счисления.
33 : 2 = 16 и 1 в остатке. Выделяем остаток.

16 : 2 = 8 и 0 в остатке. Обведём наш остаток.

8 : 2 = 4 и 0 в остатке. Снова выделяем его.

4 : 2 = 2 и 0 в остатке. Обводим остаток.

2 : 2 = 1 и ноль в остатке. И опять обводим остаток от деления.

1 : 2 = 0 и один в остатке. Выделим остаток.
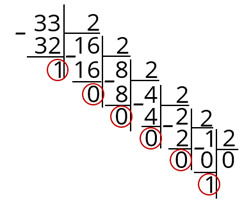
Нам осталось записать все остатки справа на лево.
3310 = 1000012.
Мы перевели число 33 в двоичную систему счисления.
Сравним число, которое получилось при сложении двоичных чисел, и число, которое получилось при переводе числа тридцать три в двоичную систему счисления.


Они равны. Это говорит о том, что мы с вами правильно провели сложение двоичных чисел.
Перейдём к умножению. Снова рассмотри таблицу.

0 ·0 = 0.
0 · 1 =0.
1 · 1 = 1.
Давайте снова разберёмся на примере. Нам даны два числа для умножения: 11012 и 10012. Запишем их в столбик.

Начнём с последней цифры второго числа, умножаем на неё первую цифру справа.

1 ·1 = 1. Запишем эту цифру под чертой.

1 · 0 = 0.

Снова запишем.

1 · 1 = 1.

1 · 1 = 1.

Ставим плюс. Берём вторую цифру 0. А записывать мы должны начинать под второй цифрой справа.

Так как мы знаем, что при умножении на 0 мы всё равно получим нули, то не будем их записывать. Далее третья справа цифра снова 0. И записывать мы должны уже под третьей цифрой.

Но так как у нас снова будут одни нули, не будем записывать эту строку. Идём дальше. Четвёртая цифра 1.
1 · 1 = 1.
Записывать будет под четвёртой цифрой справа налево.

1 · 0 = 0.

1 · 1 = 1

1 · 1 = 1

Нам осталось сложить получившиеся числа уже известным нам образом. Крайних справа 3 цифры сносим вниз, так как к ним ничего не прибавляется.

1 + 1 = 10.
0 записываем, а 1 запоминаем.

Дальше идёт 0, но у нас есть 1, которую мы запоминали, то есть 0 + 1 = 1. Запишем её.

Дальше сносим две единицы вниз, так как к ним ничего не прибавляется.

Теперь давайте проверим, правильно ли мы решили, уже известным нам способом. Переведём исходные числа в десятичную систему счисления.
Запишем первое и проставим степени для двойки справа налево.

Ставим равно и запишем следующее:

Мы получили число 13.
Теперь переведём второе число. Снова расставим степени для двойки справа налево.

Запишем следующее:

Мы получили число 9.
Теперь перемножим эти числа.
13 · 9 = 117.
Переведём это число из десятичной системы счисления в двоичную. Для этого будем использовать таблицу, так как число большое.

117 : 2 = 58 и один в остатке. Число 58 запишем в ячейку справа от числа 117, а остаток в ячейку под число 117.

58 : 2 = 29 и ноль в остатке. Заполним таблицу.

29 : 2 = 14 и один в остатке. Запишем получившиеся числа в соответствующие ячейки таблицы.

14 : 2 = 7 и ноль в остатке. Снова заполним таблицу.

7 : 2 = 3 и один в остатке. Занесём числа в соответствующие ячейки.

3 : 2 = 1 и один в остатке. Записываем числа в таблицу.

1 : 2 = 0 и один в остатке. 0 никуда записывать не будем. А 1 запишем в пустую ячейку.

Теперь осталось все остатки записать поочерёдно справа на лево.
11710 = 11101012
Мы перевели число 117 в двоичную систему.
А сейчас сравним двоичное число, которое получилось при умножении, и двоичное число, которое получилось при переводе.


Они равны. Значит мы с вами правильно перемножили двоичные числа.
Переходим к «компьютерным» системам счисления.
Как вы уже знаете, вся информация в компьютере закодирована с помощью двоичной системы счисления. В этом есть свои преимущества. Давайте рассмотрим их.
Двоичные числа представляются в компьютере с помощью достаточно простых технических элементов с двумя устойчивыми состояниями. То есть 1 означает наличие чего-либо, например, сигнала, а 0 – его отсутствие.

Представление информации посредством только двух состояний надёжно и помехоустойчиво. Это говорит о том, что в данном случае используется только два сигнала 0 и 1, и нет ничего лишнего, что обеспечивает надёжность и помехоустойчивость сигнала.
Двоичная арифметика наиболее проста. В этом мы с вами убедились, рассматривая примеры на сложение и умножение.


Существует математический аппарат, обеспечивающий логические преобразования двоичных данных. Для двоичной системы счисления существует набор операций преобразования выражений, то есть из более сложных в более простые.
При обмене информацией между компьютерами происходит передача двоичных кодов.
Для человека очень сложно пользоваться такими кодами, потому что они имеют большую длину и зрительную однородность, то есть, чтобы выделить нужный фрагмент из кода нужно его внимательно изучить, но так как он большой и в своём составе имеет только единицы и нули, это очень сложно, так как нужно очень внимательно всматриваться в каждый кусочек кода. Поэтому специалисты (программисты и инженеры) на некоторых этапах разработки, создания, настройки вычислительных систем заменяют двоичные коды на аналогичные им величины в восьмеричной или шестнадцатеричной системах счисления.

В результате этого длина исходного кода сокращается в несколько раз. Вспомните, десятичное число двести сорок семь, которое мы с вами переводили на прошлом уроке в двоичную, восьмеричную и шестнадцатеричную системы счисления.

Можно сразу заметить, что числа, представленные в восьмеричной и шестнадцатеричной системах счисления короче, чем число, представленное в двоичной системе счисления. То есть, можно сделать вывод, что замена двоичных кодов на соответствующие им величины в восьмеричной или шестнадцатеричной системах счисления приводит к удобству при их рассмотрении и анализе.
А сейчас пришла пора подвести итоги урока.
Сегодня мы с вами научились выполнять такие арифметические действия над двоичными числами, как сложение и умножение. Также узнали, что у двоичной системы, которая используется в компьютерной технике, есть ряд преимуществ:
· двоичные числа представляются в компьютере с помощью достаточно простых технических элементов с двумя устойчивыми состояниями;
· представление информации посредством только двух состояний надёжно и помехоустойчиво;
· двоичная арифметика наиболее проста;
· существует математический аппарат, обеспечивающий логические преобразования двоичных данных.

 Получите свидетельство
Получите свидетельство Вход
Вход




 11506
11506


