Восьмеричная система счисления. Шестнадцатеричная система счисления. Правило перевода целых десятичных чисел в систему счисления с основанием

Для начала вспомним, что такое позиционная система счисления.

Позиционная система счисления – это система счисления, в которой количественный эквивалент цифры зависит от её положения (позиции) в записи числа.

На этом уроке мы с вами познакомимся с восьмеричной и шестнадцатеричной системами счисления, узнаем правила перевода из восьмеричной и шестнадцатеричной систем счисления в десятичную и наоборот. Также изучим правило перевода целых десятичных чисел в систему счисления с основание q.

Начнём с восьмеричной системы счисления.

Восьмеричная система счисления – это позиционная система счисления с основанием 8. В алфавит восьмеричной системы счисления входят цифры от 0 до 7 включительно.

Мы с вами уже узнали, как записывается развёрнутая форма записи числа. Она выглядит следующим образом:

Из этой формулы можно вывести развёрнутую форму записи целого восьмеричного числа:

Посмотрим, как это выглядит на примере. Нам дано следующее число: 4153₈. Давайте распишем его по формуле. Ставим равно. Для начала проставим над цифрами степени для восьмёрки справа налево, начиная с нуля.

После равно пишем первую цифру 4 и умножаем её на 8³. Ставим плюс. Далее запишем вторую цифру 1, умноженную на 8². Снова ставим плюс. Записываем цифру 5 и умножаем её на 8¹. И плюс последняя цифра 3, умноженная на 8⁰.

Мы с вами расписали исходное число в развёрнутой форме целого восьмеричного числа.

Правило для перевода из восьмеричной системы счисления в десятичную очень простое. Достаточно расписать число в развёрнутой форме записи, а затем вычислить значение получившегося выражения.

Давайте переведём наше число из восьмеричной системы счисления в десятичную. Оно уже у нас расписано в развёрнутой записи. Нам осталось сосчитать. Обратимся к математике и распишем степени числа восемь.

Теперь осталось всё посчитать. Ставим равно.

Мы получили число 2 155. Это число представлено в десятичной системе счисления.

А теперь давайте переведём число 125 из десятичной системы счисления в восьмеричную.

Это правило похоже на перевод из десятичной в двоичную систему счисления, но в данном случае мы будем делить на число 8.

Само правило звучит следующим образом: для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное 0. В результате нужно записать в одну строку, справа налево все остатки, начиная с последнего.

Переведём наше число. Делим его на 8. Получим 15, а в остатке 5. Обведём остаток в кружок.

Теперь число 15 делим на 8. Получим 1. В остатке 7. Снова обведём это число.

1 больше 0. Значит делим число 1 на 8. Получим 0. А в остатке 1. Обводим наш остаток.

Теперь осталось после равно записать все остатки справа налево.

125₁₀ = 175₈

Мы перевели число 125 в восьмеричную систему счисления.

А теперь давайте узнаем, что такое шестнадцатеричная система счисления.

Шестнадцатеричная система счисления – это позиционная система счисления с основанием 16. В алфавит этой системы входят цифры от 0 до 9 и буквы А, B, C, D, Е, F. Эти буквы обозначают в десятичной системе числа от 10 до 15 соответственно.

Для представление целого шестнадцатеричного числа в развёрнутой форме записи нужно использовать следующую формулу:

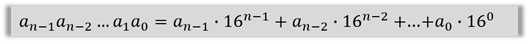
Распишем предоставленное шестнадцатеричное число A6E в развёрнутой форме.

Ставим знак равно. Снова проставим степени для шестнадцати над цифрами нашего числа справа налево.

Пишем букву А и умножаем её на 16². Ставим плюс. Пишем цифру 6, умноженную на 16¹ и прибавляем букву Е, умноженную на 16⁰.

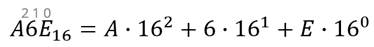
Для перевода целого шестнадцатеричного числа в десятичную систему счисления нужно перейти к его развёрнутой записи, заменить буквы на соответствующие им цифры в десятичной системе счисления и вычислить значение получившегося выражения.

Наше число уже записано в развёрнутой форме. Нам осталось заменить буквы на соответствующие им десятичной системе числа и сосчитать. Ставим равно. Буква А соответствует числу 10 в десятичной системе счисления. Запишем число 10 и умножаем его на 16².

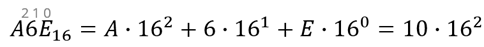
Ставим плюс и перепишем число 6, умноженное на 16¹.

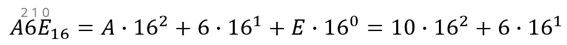
Снова ставим плюс. Букве Е соответствует число 14 в десятичной системе счисления. Пишем число 14, умноженное на 16⁰. Ставим равно.

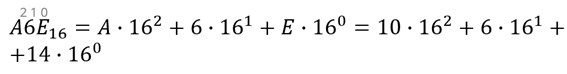
Прежде, чем всё это сосчитать снова обратимся к математике и распишем степени числа шестнадцать.

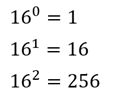
16² = 256.

16² ·10 = 2 560

Ставим плюс.

16¹ = 16.

16¹ · 6 = 96.

Снова ставим плюс.

16⁰ = 1.

16⁰ · 14 = 14.

Ставим равно.

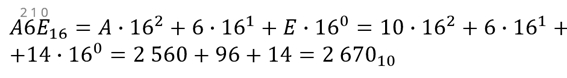
Мы получили 2 670 в десятичной системе счисления.

Для перевода целого десятичного числа в шестнадцатеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 16 до тех пор, пока не получим частное, равное 0. В результате нужно записать в одну строку, справа налево все остатки, начиная с последнего, при необходимости, заменяя цифры на соответствующие им буквы в шестнадцатеричной системе счисления.

Переведём число 350 в шестнадцатеричную систему счисления.

Делим наше число на 16, получим 21, остаток 14. Выделим его.

Делим 21 на 16. Получим 1 и 5 в остатке. Обводим наш остаток.

1 больше 0. Делим 1 на 16, получим 0 и 1 в остатке. И снова выделяем остаток 1.

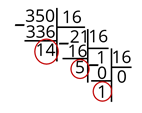
Теперь запишем все числа справа налево. Записываем следующие цифры: 1, 5.

350₁₀ = 15.

Так как в шестнадцатеричной системе счисления числу 14 соответствует буква Е, то пишем её после 5.

350₁₀ = 15E₁₆.

Мы с вами перевели число 350 в шестнадцатеричную систему счисления.

Вы, наверное, заметили, что все правила перевода целого десятичного числа в любую систему счислению с другим основанием похожи.

Давайте изучим общее правило перевода целых десятичных чисел в любую систему счисления с основание q.

Для того, чтобы перевести целое десятичное число в систему счисления с основанием q нужно:

1. Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, равное нулю.

2. Полученные остатки, которые являются цифрами числа в новой системе счисления, привести в соответствии с алфавитом новой системы счисления.

3. Составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.

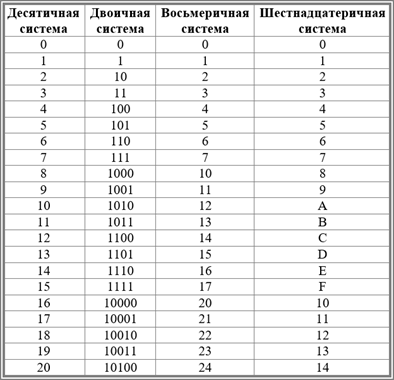
Вам предоставлена таблица соответствия десятичных, двоичных, восьмеричных и шестнадцатеричных чисел от 0 до 20. Числа от 0 до 20 подразумевают собой десятичную систему счисления.

А теперь давайте выполним задание.

Переведём одно и то же число 247 в двоичную, восьмеричную и шестнадцатеричную системы счисления и сравним получившиеся числа.

Для начала переведём из десятичной в двоичную систему счисления. Для этого будем использовать таблицу, так как число большое. В ней будет две строки. В первую строку первого столбца запишем наше число.

Делим его на 2. Получим 123 и 1 в остатке. 123 запишем во вторую ячейку первой строки, а 1 – в первую ячейку второй строки.

Далее 123 разделить на 2 и получим 61 и 1 в остатке. 61 запишем после числа 123, а остаток один под число 123.

Далее 61 : 2 = 30 и остаток – 1. Запишем их в таблицу.

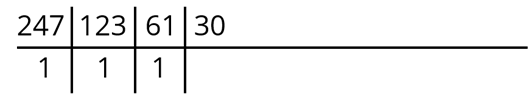
30 : 2 = 15, а остаток равен 0. Снова запишем их в таблицу в соответствующие ячейки.

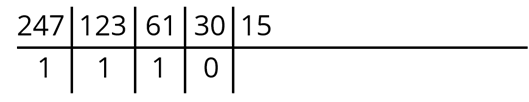
При делении 15 на 2 получим 7 и 1 в остатке. Снова заполняем таблицу.

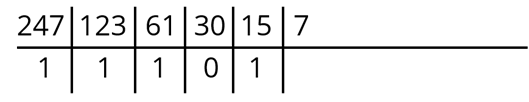
Далее 7 : 2 = 3 и 1 в остатке. Запишем в соответствующие ячейки наши числа.

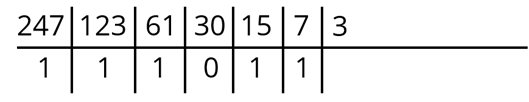
3 :2 = 1 и 1 в остатке. Занесём данные в таблицу.

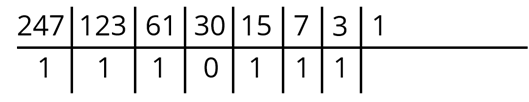
И делим 1 на 2, получим 0 и 1 в остатке. 0 писать не будет. Занесём только наш остаток в ячейку.

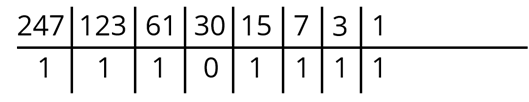
А теперь соберём все наши цифры в число в двоичной системе. Записываем их поочерёдно справа налево.

247₁₀ = 11110111₂.

А сейчас переходим к переводу в восьмеричную систему счисления числа 247.

Делим 247 на 8. Получим 30 и 7 в остатке. Обведём остаток от деления.

Далее 30 делим на 8, получим 3 и 6 в остатке. Выделяем остаток.

3 делим на 8, получаем 0 и 3 в остатке. Обводим остаток.

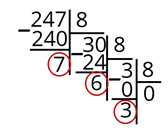
Теперь запишем все остатки справа налево и получим число в восьмеричной системе счисления.

247₁₀ = 367₈.

Нам осталось перевести наше число в шестнадцатеричную систему счисления. Делим 247 на 16. Получим 15 и 7 в остатке. Обведём остаток.

Теперь делим 15 на 16, получим 0. А остаток от деления равен 15. Выделим его.

А сейчас запишем наши цифры справа налево в соответствии с алфавитом шестнадцатеричной системы счисления. Число 15 — это буква F в этой системе счисления. Ставим её на первое место. А затем пишем число 7.

247₁₀ = F7₁₆

Задание выполнено. Давайте сравним все наши получившиеся числа.

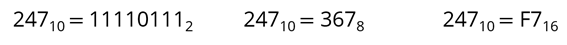
Как можем видеть – все они одинаковые, но записаны разными цифрами, потому что они представлены в различных системах счисления. Это можно увидеть, если обратить внимание на основания чисел.

А теперь пришла пора довести итоги урока. Сегодня мы узнали, что такое восьмеричная и шестнадцатеричная системы счисления, какие действия нужно выполнить для перевода целого десятичного числа в систему счисления с основанием q.

Также мы сегодня научились переводить числа из восьмеричной и шестнадцатеричной систем счисления в десятичную и наоборот.