Общие сведения о системах счисления. Двоичная система счисления

В современной жизни человек постоянно сталкивается с числами. К примерам можно отнести номера телефонов, цены в магазинах, адреса проживания и много другое.

На протяжение долгого времени у каждого народа формировалось своё написание чисел, с помощью которых они писали и считали. Но принципы записи чисел были совершенно другими, не такими, как сейчас.

В наше время для записи числа человек использует десятичную систему счисления.

На этом уроке мы с вами узнаем, что такое система счисления, какие существуют разновидности систем счисления, а также подробно остановимся на двоичной системе счисления.

Итак, система счисления – это знаковая система, в которой приняты определённые правила записи чисел.

Цифры – это знаки, с помощью которых записываются числа.

Алфавит системы счисления – это совокупность цифр.

В любой системе счисления цифры служат для обозначения чисел, которые называются узловыми.

Остальные числа, которые называются алгоритмическими, получаются в результате каких-либо операций из узловых чисел.

Давайте разберёмся на примере.

Рассмотрим вавилонскую систему счисления. В ней узловыми являлись числа один, десять и шестьдесят.

Чтобы досчитать до девяти нужно было поставить девять единичек.

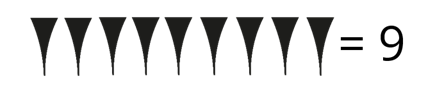
Например, число пятнадцать будет состоять из десяти и пяти единичек.

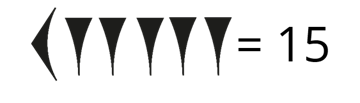
Число двадцать будет состоять из двух десяток и так далее.

А теперь перейдём к видам систем счисления. Системы счисления различаются выбором узловых чисел и способами образования алгоритмических чисел. Можно выделить унарную, непозиционные и позиционные системы счисления.

Унарная система счисления – это самая древняя и простейшая система счисления. В качестве единственной цифры в ней используется единица. Она может быть изображена в виде чёрточки, камушка, палочки и так далее.

Длина записи числа при таком кодировании прямо связана с его величиной. Эта система счисления используется для обучения детей счёту, при подсчёте голосов на выборах в маленьких группах, в домино при подсчёте очков.

Такую систему счисления использовал Робинзон Крузо в виде зарубок на дереве для ведения календаря на необитаемом острове.

Переходим к непозиционным системам счисления.

Непозиционная система счисления – это система счисления, в которой количественный эквивалент (количество значений) цифры в числе не зависит от её положения в записи числа.

То есть можно сказать, что каждая цифра имеет своё значение, и от перестановки местами таких цифр значение числа не меняется.

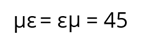
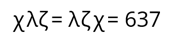
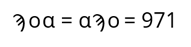
В большинстве таких систем числа образуются путём сложения узловых чисел.

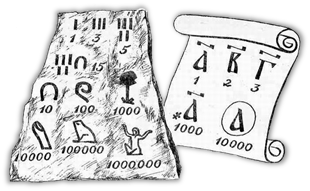
К примерам таких систем относится египетская система. Рассмотрим её.

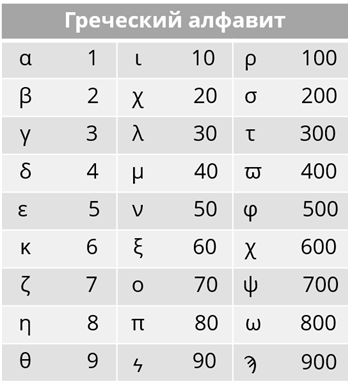
Вам предоставлена таблица с символами и с их значениями. В этой системе счисления числа, которые не являлись степенью десяти, записывались путём повторения этих цифр. Каждая цифра могла повторяться от одного до девяти раз. Например, число две тысячи триста пятьдесят шесть будет выглядеть следующим образом.

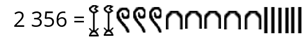
Определённого порядка в записи числа нет. Числа могли записываться слева направо или справа налево и даже вертикально.

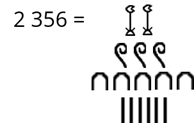
Например, две следующие иероглифические записи обозначают одно и то же число – двенадцать.

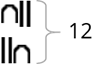
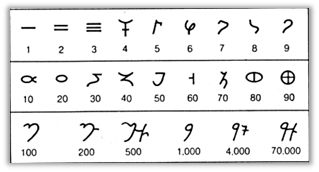
Римская система счисления также относится к непозиционным. Рассмотрим таблицу с обозначениями чисел.

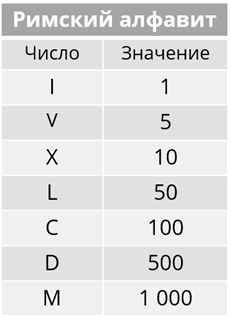
В этой системе числа получаются путём сложения и вычитания узловых чисел.

Для подсчёта следует придерживаться определённого правила: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитает его.

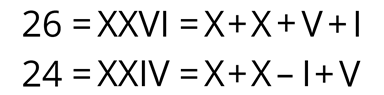
Позиционная система счисления – это система счисления, в которой количественный эквивалент цифры зависит от её положения (позиции) в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.

То есть, можно сказать, что один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места, где он расположен.

К примеру позиционной системы счисления относится десятичная, которой мы привыкли пользоваться в повседневной жизни.

Десятичная система счисления – это позиционная система по целочисленному основанию десять. Она является одной из наиболее распространённых систем. В ней используются цифры от 0 до 9. Эти цифры называются арабскими.

Есть предположение, что основание системы, число 10 связано с количеством пальцев на руках у человека.

Алгоритмические числа образуются в ней следующим образом: значения цифр умножаются на «веса» соответствующих разрядов, и все полученные значения складываются. Мы с вами знаем следующие виды разрядов: единицы, десятки, сотни и так далее. Число сто двадцать три получается следующим образом:

Основанием позиционной системы счисления может служить любое натуральное число q > 1. Алфавитом позиционной системы счисления с основанием q служат числа 0, 1 … q – 1, каждое из которых может быть записано с помощью одного уникального символа. Младшей цифрой всегда будет являться 0.

Разберёмся на примере. Нам дана знакомая всем десятичная система счисления. То есть q=10. Алфавитом этой системы будут цифры от 0 до q – 1. То есть q – 1 = 9. Получим следующие цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Если сосчитать их, то получится 10.

При кодировании информации в компьютере используется двоичная система. То есть q=2. Цифры, которые входят в эту систему будут начинаться с 0 и до q – 1.

2 – 1 = 1. Соответственно в двоичной системе счисления будет использоваться алфавит из двух цифр 0 и 1.

В позиционной системе счисления с основанием q любое число можно представить в виде:

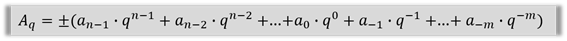
А – это само число.

q – основание системы счисления.

a_i – цифры, принадлежащие алфавиту данной системы счисления.

n – количество целых разрядов числа.

m – количество дробных разрядов числа.

qⁱ – «вес» итого разряда.

Наша формула записана в развёрнутом виде. Свёрнутая форма записи числа – это представление числа в следующем виде:

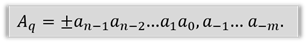
Разберёмся на примере. Итак, перед нами представлено число 1 675,21 в свёрнутой форме.

Записано это число в десятичной системе счисления. Давайте распишем это число и посмотрим, как оно выглядит в развёрнутой форме.

Поставим знак равно. Из условия понятно, что q=10. Остаётся определиться с n. Для этого расставим над цифрами числа, которые будут обозначать степень числа q в развёрнутой записи числа. Обратимся к математике. Запишем степени числа десять.

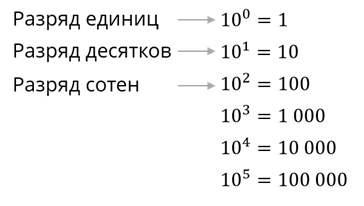
Из этой записи видно, что разряд единиц соответствует нулевой степени числа десять, разряд десятков соответствует первой степени числа десять и так далее. Запишем эти степени над цифрами нашего числа.

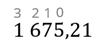
Над цифрами, которые располагаются после запятой, поставим числа минус один и минус два.

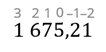
Теперь мы можем записать развёрнутую форму нашего числа.

a_{n – 1} – это первая цифра нашего числа, то есть 1. Она умножается на q^{n – 1}, то есть на 10³. Ставим плюс. a_{n – 2} – это вторая цифра нашего числа, то есть 6. Умножаем её на 10². Аналогичным образом распишем всё число.

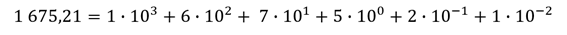
Нам не привычно видеть его таким, но это – развёрнутая форма записи числа 1 675,21.

А сейчас давайте перейдём к двоичной системе счисления. Двоичная система счисления – это позиционная система счисления с основанием два. Как мы уже знаем, для записи чисел в этой системе используются только две цифры: 0 и 1. Например, число 16 в двоичной системе счисления будет выглядеть следующим образом: .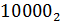

Для обозначения системы счисления, в которой представляется число, используется нижний индекс, указывающий на основание системы.

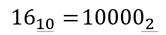
Так мы можем сразу видеть, что число 16 записано в десятичной системе, а второе – в двоичной.

Формула развёрнутой формы записи числа для целых двоичных чисел будет выглядеть следующим образом:

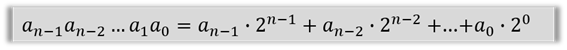
Из этой формулы можно вывести правило перевода натуральных двоичных чисел в десятичную систему счисления: необходимо вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.

Давайте проверим и переведём следующее число 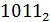 из двоичной системы счисления в десятичную. Для начала над всеми цифрами напишем степени для q начиная с 0 справа налево.

Ставим равно. Пишем первую 1 и умножаем её на 2³, прибавляем 0, умноженный на 2², затем прибавим 1, умноженную на 2¹ и 1, умноженную на 2⁰.

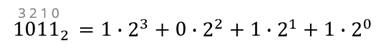
Ставим равно и посчитаем всё это.

1 · 2³ = 8.

Ставим плюс.

0 · 2² = 0.

1 · 2¹ = 2.

1 · 2⁰ = 1.

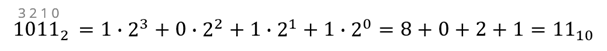
Посчитав это всё получим число одиннадцать в десятичной системе счисления.

Для закрепления давайте переведём ещё одно число 10001₂ из двоичной в десятичную систему счисления. Но перед этим запишем чему равны степени числа два.

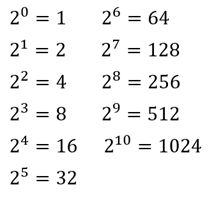
Итак, снова проставляем степени начиная с нуля справа налево.

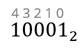
Ставим равно. После равно слаживаем цифры, умноженные на два в соответствующей степени.

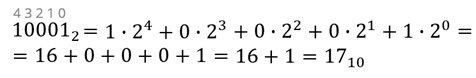
После подсчёта получим число семнадцать.

Для перевода чисел из десятичной системы счисления в двоичную, нужно делить число на 2. Если полученное частное больше нуля, то его снова необходимо разделить на два и т. д., пока частное не станет равным 0. В результате нужно записать в одну строку, справа налево все остатки, начиная с последнего.

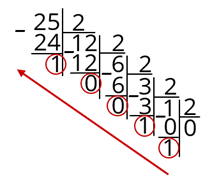
Давайте посмотрим на примерах, как это делается. Переведём число 25 из десятичной системы счисления в двоичную. Будем делить в столбик. Итак, делим 25 на 2. Получится 12, а в остатке 1.

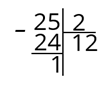
Теперь число 12 делим на 2. Получается 6, а в остатке 0.

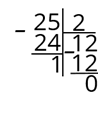
Делим число 6 на 2, получаем 3, а в остатке 0.

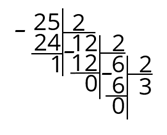
Далее разделим 3 на 2, получим 1 и 1 в остатке.

Делим 1 на 2, получим 0 и 1 в остатке.

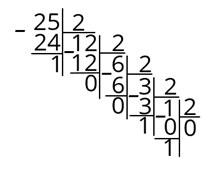
Больше число не будет делиться на цело. А теперь обведём все наши остатки.

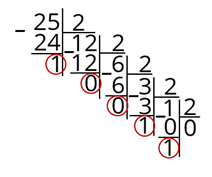
Они нам понадобятся для записи числа в двоичной системе счисления. Записывать их будем справа налево.

Первая идёт 1. Запишем её.

25₁₀ = 1

Затем идёт ещё одна 1 из остатка, также её запишем.

25₁₀ = 11

Аналогично перепишем все наши остатки в одну строку.

25₁₀ = 11001₂

Мы перевели с вами число двадцать пять из десятичной системы счисления в двоичную.

Если число большое, то будет более удобно представить его в виде таблицы.

Давайте посмотрим, как это можно сделать. Переведём число 142 в двоичную систему счисления. Наша таблица будет содержать две строки. В первой будем записывать число, которое получается при делении на 2, а во второй остаток. Итак, в первой строке первого столбца запишем число 142.

При делении этого числа на 2 получим 71 и 0 в остатке. Число 71 запишем во второй столбец первой строки, а остаток в первый столбец второй строки.

Делим 71 на 2. Получим 35 и 1 в остатке. 35 запишем в третью ячейку первой строки, а остаток 1 во вторую ячейку второй строки.

35 : 2 = 17 и 1 в остатке. 17 запишем в следующую ячейку после 35, а остаток – под число 35.

Далее 17 делим на 2 получим 8 и 1 в остатке. Запишем наши числа в соответствующие ячейки.

8 :2 = 4 и 0 остаток. Заполним таблицу.

4 :2 = 2 и 0 в остатке. Также запишем их.

2 :2 = 1 и 0 в остатке. Пишем 1 в следующую ячейку после 2, а под 2 запишем 0.

Делим 1 на 2 получим 0 и 1 в остатке. Не будем наш 0 записывать в таблицу. Внесём в неё только остаток от деления – 1 в соответствующую ячейку.

Теперь нам осталось записать наше число в строку. Для этого перепишем все числа, которые находятся во второй строке, справа налево и получим следующее:

141₁₀ = 10001110₂

Мы перевели число 142 из десятичной системы счисления в двоичную.

Пришла пора подвести итоги урока.

Сегодня мы узнали, что такое система счисления, познакомились с унарной, непозиционными и позиционными системами счисления. Также мы научились переводить из двоичной системы счисления в десятичную и наоборот.