Подмножества

Прежде чем приступить к рассмотрению новой темы, напомним, что множество – понятие начальное, поэтому точно сказать, что это такое, нельзя. Множество нужно понимать как совокупность каких-либо объектов (элементов), объединённых по некоторому признаку.

Множество можно записать одним из двух способов.

Первый способ. Можно явно перечислить все элементы множества.

Второй способ. Можно описать множество, то есть указать признак, которым обладают все элементы этого множества.

Например, множество результатов бросания игрального кубика можно записать перечислением в фигурных скобках: .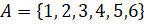

Напомним, что множества обозначают большими буквами латинского алфавита.

Чтобы указать, что некоторый элемент принадлежит множеству, используют значок . Например, .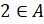

Несмотря на то, что слово «множество» намекает, что элементов может быть много, во множестве может быть только один элемент. Более того, множество может быть пустым, то есть не иметь элементов вовсе.

Пустое множество – это множество, которое не содержит элементов.

Поговорим о подмножествах.

Пример. Пусть  – множество всех треугольников, а  – множество равносторонних треугольников. Каждый равносторонний треугольник является треугольником. А значит, можно сказать, что множество  включается во множество  или что множество  включает в себя множество БЭ. Также в таком случае говорят, что множество  является подмножеством множества  и записывают . Это означает, что все элементы множества  являются элементами множества .

Множество  называется подмножеством множества , если любой элемент множества  принадлежит множеству .

Пример. Пусть  – множество всех прямоугольников, а  – множество квадратов. Так как каждый квадрат является прямоугольником, то можно сказать, что множество  является подмножеством множества .

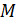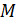Пример. Пусть  – множество всех учеников класса,  – множество девочек этого класса,  – множество мальчиков этого класса. Тогда можно сказать, что множество  является подмножеством множества  и множество  является подмножеством множества .

Пример. Пусть  – множество натуральных чисел от 1 до 3.

Его можно записать .

У этого множества 8 подмножеств. Посмотрите на граф, где изображены все 8 подмножеств множества .

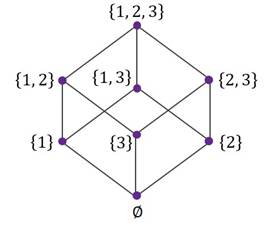
Рёбра этого графа соединяют каждую вершину-множество со всеми его подмножествами на следующем уровне. Двигаясь вниз по рёбрам, можно пройти от каждого множества ко всем его подмножествам. Этот граф напоминает нам кубик.

Обратите внимание, что само множество А является подмножеством и пустое множество тоже является подмножеством.

Запомните! Пустое множество является подмножеством любого множества. Любое множество является подмножеством самого себя. Поэтому, каково бы ни было множество , можно записать: 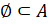 и .

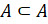Может показаться, что утверждение «пустое множество является подмножеством множества » противоречит определению подмножества, так как в определении говорится, что любой элемент подмножества является элементом самого множества. Но ведь пустое множество не содержит элементов. Давайте разбираться.

Перепишем утверждение «пустое множество является подмножеством множества ».

«Если элемент принадлежит пустому множеству, то он принадлежит множеству ».

Посылка «элемент принадлежит пустому множеству» – ложна. А из лжи, как мы знаем, следует что угодно. Поэтому утверждение «пустое множество является подмножеством множества » является истинным высказыванием.

Мы доказали данное утверждение, пользуясь законами логики.

Давайте выполним несколько заданий.

Задание первое. Какие из следующих множеств являются пустыми?

Решение. Множество  состоит из одного элемента, а значит, не является пустым.

Множество натуральных чисел меньше 1 является пустым, так как натуральные числа – это числа, которые используются при счёте.

Множество квадратов, имеющих тупой угол, тоже является пустым, так у квадрата все углы равны 90º.

Отметим, что каждое из этих пустых множеств является подмножеством любого множества.

Задание второе. Пусть множество  состоит из результатов броска монеты. Выпишите все подмножества этого множества.

Решение. При подбрасывании монеты может выпасть либо орёл, либо решка.

Запишем множество  перечислением его элементов в фигурных скобках.

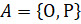
Каково бы ни было множество, его подмножествами являются пустое множество и само это множество.

, .

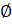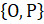Также подмножествами множества  являются ещё два множества, каждое из которых состоит из одного элемента.

, .

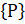Мы выписали все подмножества множества . Получается, что у него их четыре.

Задание третье. Пусть  – множество делителей числа 12, а  – множество делителей числа 6. Является ли одно из множеств подмножеством другого?

Решение. Делителями числа 12 являются 6 чисел.

Делителями числа 6 являются 4 числа.

Видим, что любой элемент множества  принадлежит множеству , а значит, множество  является подмножеством множества .

До встречи на наших следующих занятиях!