Представим себе такую историю…
– Саша, чем ты занимаешься? – поинтересовался Паша.
– Нам по математике задали разгадать ребус, по которому мы узнаем тему нашего следующего урока, – ответил Саша. — А в этом ребусе так много картинок, букв и разных запятых, что я совсем запутался.
– Не расстраивайся! – подбодрил друга Паша. – Я помогу тебе. Показывай свой ребус.
– Вот, смотри, какое длиннющее слово! – воскликнул Саша. – Здесь и перевёрнутый стол нарисован, и окно, и сани, буквы и запятые.

– Саша, да это совсем лёгкий ребус, – возразил Паша, – и не обязательно должно получиться длиннющее слово. Сейчас мы быстренько всё разгадаем. Итак, запятые в ребусе означают, что из названия картинки нужно исключить столько букв, сколько стоит запятых. Если запятые стоят перед картинкой, то убираем буквы в начале слова, если после – в конце слова, – вспомнил Паша. – Если картинка перевёрнута вверх ногами, это значит, что слово читается задом наперёд. Плюс у нас тут ещё нарисованы запятые. Значит, в перевёрнутом слове нужно исключить первую и последнюю буквы. Что тогда получится?
– У нас нарисован стол, – начал размышлять Саша. – Задом наперёд это слово читается так: «лотс». Затем исключим первую и последнюю буквы. И останется у нас «от».
– Отлично! – поддержал друга Паша. – Идём дальше. Здесь нарисовано окно и перед картинкой стоят 2 запятые. Что за слово получится?
– Было окно, а останется только «но», – сказал Саша.
– Верно! – согласился Паша. – Затем у нас в ребусе идут буквы «ш» и «е», значит, мы их просто добавим к предыдущим словам в порядке их следования. Перейдём к следующей картинке.
– У нас нарисованы сани, – начал размышлять Саша. – А перед картинкой стоят 2 запятые. Значит, исключим первые 2 буквы. И останется у нас «ни».
– Молодец! – обрадовался за друга Паша. – И останется только добавить к окончательному слову ещё букву «е». Попробуй из получившихся слогов и букв составить единое слово.
– Так, – начал Саша, – у нас есть слоги «от», «но», буквы «ш», «е», слог «ни» и буква «е». Подумаем… Так это же «отношение»!

– Молодец, Саша! – похвалил друга Паша. — Значит, на уроке математики вы будете знакомиться с отношениями!
– Интересно, что это за отношения такие? – спросил Саша.
– А давай спросим у Мудряша, – предложил Паша. – Он точно сможет объяснить.
– Ребята, прежде чем я расскажу вам об отношениях, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!
–
Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – На уроках русского
языка вы познакомились со словами, которые называют синонимами. Напомню,
так называют слова, которые имеют одинаковые значения, но по-разному звучат и
пишутся. Например, слова «урок» и «занятие», «учитель» и «педагог», «трудный» и
«тяжёлый», «друг» и «приятель» близки по значению. Так вот, оказывается, и в
математике тоже встречаются слова-синонимы. Например, вы уже знакомы с такими
математическими синонимами, как вторая степень числа и квадрат числа,
один процент величины и одна сотая величины, луч и полупрямая.
Но есть и ещё один пример такого рода, о котором мы сейчас и поговорим. Давайте
рассмотрим следующие две записи:  и
и  . Прочитайте их.
. Прочитайте их.
– В первом случае у нас записано частное трёх и четырёх – сказал Паша.
– А во втором дробь три четвёртых, – продолжил Саша.
– Но ведь черту дроби можно рассматривать как знак деления, – заметил Паша. – А значит, дробь три четвёртых можно прочитать и как «три разделить на четыре», то есть снова имеем дело с частным двух чисел.
– Вы очень внимательные! – похвалил ребят Мудряш. – А ещё эти две записи можно прочитать как «отношение двух чисел». То есть частное и отношение в математике – это действия-синонимы, их записи разные, но означают они одно и то же действие.

–
Запомните! – продолжил Мудряш. – Частное двух чисел 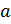 и
и
 , отличных от нуля,
называют отношением чисел
, отличных от нуля,
называют отношением чисел 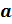 и
и  или
отношением числа
или
отношением числа 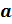 к числу
к числу  .
.
– Тогда наши записи ещё можно прочитать как отношение числа три к числу четыре? – спросили мальчишки.

– Всё правильно! – согласился Мудряш. – Прочитайте следующие записи, применяя наше новое слово.
– Первую запись можно прочитать как отношение числа 15 к числу 5, – начал Саша.
– Вторую запись можно прочитать как отношение числа 5 к числу 7, – продолжил Паша.
–
Следующую запись можно прочитать как отношение числа  к числу
к числу  , – сказал Саша.
, – сказал Саша.
– А последнюю запись можно прочитать как отношение числа 0,5 к числу 0,12.

–
Молодцы! – похвалил ребят Мудряш. – Вы уже вспоминали, что при записи деления
натуральных чисел вместо знака деления можно использовать дробную черту. То
есть отношение двух натуральных чисел 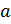 и
и  можно
записать в виде дроби
можно
записать в виде дроби  .
.

Также
договорились использовать черту дроби и в тех случаях, когда 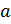 и
и
 – дробные числа.
Например, отношение числа 0,4 к числу 2,4 можно записать и так:
– дробные числа.
Например, отношение числа 0,4 к числу 2,4 можно записать и так:  .
.

–
Тогда получается, что отношение чисел 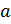 и
и  можно
записать двумя способами? – решили уточнить мальчишки.
можно
записать двумя способами? – решили уточнить мальчишки.
–
Правильно! – сказал Мудряш. – Правда, не во всех случаях запись отношения
дробью уместна. Например, запись отношения числа  к числу
к числу  в виде вот такой двухэтажной
дроби не удобна
в виде вот такой двухэтажной
дроби не удобна  . Поэтому выбор способа
записи чаще всего определяется её компактностью.
. Поэтому выбор способа
записи чаще всего определяется её компактностью.

–
Запомните! – продолжил Мудряш. – В отношении числа 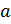 к
числу
к
числу  числа
числа 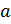 и
и
 называют членами
отношения, число
называют членами
отношения, число 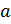 – предыдущим членом
отношения, а число
– предыдущим членом
отношения, а число  – последующим. Если
– последующим. Если
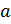 и
и  –
натуральные числа, то, записав их в виде отношения
–
натуральные числа, то, записав их в виде отношения  , на основании основного
свойства дроби можно сделать следующий вывод:
, на основании основного
свойства дроби можно сделать следующий вывод:
отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю. Это свойство называют основным свойством отношения. Оно остаётся справедливым и в тех случаях, когда члены отношения – дробные числа.
–
Давайте рассмотрим следующие отношения дробных чисел: 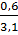 ,
,  ,
,  , – предложил Мудряш. – Применяя
основное свойство отношения, можно члены первого отношения умножить на 10, тогда
получим отношение числа 6 к числу 31.
, – предложил Мудряш. – Применяя
основное свойство отношения, можно члены первого отношения умножить на 10, тогда
получим отношение числа 6 к числу 31.
– А если члены второго отношения умножить на их наименьший общий знаменатель – число 10, – начал Саша, – то получим отношение числа 8 к числу 7.
– Тогда можно умножить члены последнего отношения тоже на 10, – продолжил Паша, – в результате получим отношение числа 24 к числу 5.

– Всё правильно! – согласился Мудряш. – Исходя из этого, можем сделать следующий вывод: отношение дробных чисел можно заменить отношением натуральных чисел.
– Очень часто отношение используют при сравнении двух величин, – продолжил Мудряш. – Посмотрите: у нас изображены два отрезка. Отрезок АВ длиной 9 сантиметров и CD, длина которого 60 миллиметров. Скажите, чему равно отношение длины отрезка АВ к длине отрезка CD?
– Это отношение будет равно 9 к 60, – ответил Саша.
– Неправильно! – сказал Мудряш. – Сделаем важное замечание: если значения двух величин выражены разными единицами измерения, то для нахождения отношения этих величин надо предварительно перейти к одной единице измерения.
– Так как 60 миллиметров — это 6 сантиметров, то отношение длины отрезка АВ к длине отрезка CD будет равно 9 к 6, или 1,5, – пересчитал Саша.
–
Теперь правильно! – согласился Мудряш. – Это отношение показывает, что длина
отрезка АВ составляет  длины отрезка CD.
А тогда чему равно отношение длины отрезка CD
к длине отрезка АВ?
длины отрезка CD.
А тогда чему равно отношение длины отрезка CD
к длине отрезка АВ?
–
Это отношение будет равно 6 к 9, или  , – ответил Паша.
, – ответил Паша.
–
Верно! – согласился Мудряш. – Это отношение показывает, что длина отрезка CD
составляет  длины отрезка АВ.
длины отрезка АВ.

Тогда
можем сделать следующий вывод. Запомните! Отношение чисел 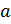 и
и
 показывает, во
сколько раз число
показывает, во
сколько раз число 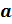 больше числа
больше числа  или какую часть число
или какую часть число
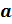 составляет от
числа
составляет от
числа  .
.
– Кстати, в виде отношений можно определить и другие величины, – продолжил Мудряш. – Например, скорость. Это ведь ничто иное, как отношение длины пройденного пути ко времени, за которое пройден этот путь. В свою очередь, цена – это отношение стоимости товара к количеству единиц его измерения (килограммов, литров, метров, коробок и так далее). Отношением можно определить и производительность труда. Ведь это ничто иное, как отношение объёма выполненной работы ко времени, за которое выполняется эта работа.

Кстати, отношение величин одного наименования (например, длин, скоростей, стоимостей и так далее, выраженных одинаковыми единицами измерения) есть число. Такие величины называют однородными. А вот отношение величин разных наименований (например, пути и времени, стоимости товара и его количества так далее) есть новая величина.

– Существует и ещё один очень интересный вид отношений, – продолжил Мудряш. – Изображая на бумаге участок земной поверхности, машину, дом, жилую комнату, мы вынуждены изменять их реальные размеры. Ведь мы же не можем нарисовать, например, дом в его реальную величину.
А чтобы представления об изображаемых объектах были правильными на картах, чертежах и планах, все размеры уменьшают (или увеличивают) в одно и то же число раз и указывают, во сколько раз изображение некоторого отрезка меньше (больше) этого отрезка в реальности. Другими словами, на карте, плане, чертеже указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше (больше) длины соответствующего отрезка в реальности. Это отношение называют масштабом.

Давайте разберёмся, что же такое масштаб.
– Итак, на экране вы видите карту, масштаб которой равен 1 к 10 000 000. Это означает, что 1 сантиметр на карте соответствует 10 000 000 сантиметров на местности, что составляет 100 километров.

Давайте попробуем с помощью этой карты определить расстояние от Москвы до Костромы.
– Я знаю, как это сделать, – воскликнул Паша. – Нам надо линейкой измерить расстояние между точками, изображающими указанные города. В нашем случае расстояние между точками равно 3 сантиметрам.
– Молодец! – похвалил Пашу Мудряш. – Полученную величину 3 сантиметра следует умножить на 10 000 000.
– Тогда расстояние между Москвой и Костромой равно 30 000 000 сантиметров, или 300 километрам, – посчитал Саша.


 Получите свидетельство
Получите свидетельство Вход
Вход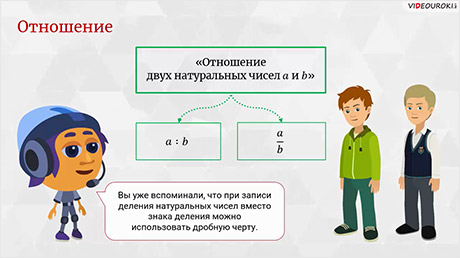



 0
0 2468
2468