Десятичное приближение обыкновенной дроби

Представим себе такую историю…

– Саша, чем ты занимаешься? – поинтересовался у друга Паша.

– Да я сегодня катался на велосипеде, – начал Саша. – Представляешь, я проехал 43 километра за 3 часа.

– Ну ты и гоняешь! – удивился Паша.

– Вот решил посчитать, с какой скоростью я проехал свой путь, – задумался Саша.

– Ну, тут же нет ничего сложного, – сказал Паша. – Чтобы найти скорость, нужно расстояние разделить на время.

– Да, я уже поделил всё, – сказал Саша, – но число какое-то уж слишком большое получилось.

– И какая же скорость у тебя вышла? – спросил Паша.

– Вот, смотри, – ответил Саша, – получилось, что я ехал со скоростью 14,333…

– Да уж! И вправду странная скорость вышла, – задумался Паша. – Помнишь, мы научились округлять натуральные числа и десятичные дроби? Может, и бесконечные периодические дроби можно тоже как-нибудь округлить? Давай спросим у Мудряша.

– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Выполняя вычисления с бесконечными периодическими дробями, удобно пользоваться их приближениями, которые получают при округлении бесконечных десятичных дробей до определённого разряда. В результате округления получается конечная десятичная дробь, которую называют десятичным приближением обыкновенной дроби. Число, которое образуется после округления, тем точнее, чем больше десятичных знаков в приближении.

– А ты научишь нас округлять бесконечные периодические дроби? – спросили мальчишки.

– Конечно! – согласился Мудряш. – Но для начала давайте вспомним, как мы округляли десятичные дроби. И давайте для примера округлим следующие десятичные дроби:  – до десятых;  – до сотых.

– Первая дробь — 152,268, – начал Саша. – Нужно округлить её до десятых. Мы помним, что для того, чтобы десятичную дробь округлить до единиц, десятых, сотых и так далее, надо все следующие за этим разрядом цифры отбросить. Если первая из отбрасываемых цифр равна 5, 6, 7, 8 или 9, то последняя из оставшихся цифр увеличивается на 1. Чтобы округлить до десятых, нам нужно откинуть последние 2 цифры. Первая цифра, которую мы откинули, равна 6, значит, цифру в разряде десятых увеличим на 1. Получим 152,3.

– Вторая дробь — 42,35154, – продолжил Паша. – Эту дробь нам нужно округлить до сотых. Чтобы десятичную дробь округлить до нужного разряда, надо все следующие за этим разрядом цифры отбросить. Если при этом первая из цифр, которые мы отбрасываем, равна 0, 1, 2, 3 или 4, то последняя из оставшихся цифр не меняется. Итак, отбросим последние 3 цифры. Первая отбрасываемая цифра равна 1, значит, увеличивать цифру 5 не надо. Получим 42,35.

– Молодцы! – похвалил ребят Мудряш. – Точно так же округляют и бесконечные периодические десятичные дроби, «отсекая» в определённом месте «бесконечный хвост». Чтобы разобраться, как округляют периодические дроби, давайте преобразуем обыкновенную дробь  в периодическую. А затем округлим полученную периодическую дробь до единиц, десятых, сотых и тысячных.

– Это неправильная дробь, – начал Саша, – так как числитель больше знаменателя. Выделим целую часть. Получим смешанное число .

– Теперь выполним деление уголком числителя на знаменатель, – продолжил Паша. –  В результате получим периодическую дробь 1,58(3).

– А теперь перейдём к округлению, – сказал Саша. – Сначала нам нужно эту периодическую дробь округлить до единиц. Для этого нам нужно отбросить все цифры, которые стоят после целой части. Первая отбрасываемая цифра равна 5, значит, цифру в разряде единиц увеличим на 1. Получим 2.

– Затем округлим полученную периодическую дробь до десятых, – продолжил Паша. – Нам нужно откинуть все цифры, которые стоят после разряда десятых. Первая из отбрасываемых цифр равна 8. Значит, цифру в разряде десятых увеличим на 1. Получим десятичную дробь 1,6.

– Теперь округлим нашу периодическую дробь до сотых, – сказал Саша. – Отбрасываем все цифры, которые стоят после разряда сотых. Первая отбрасываемая цифра равна 3. Значит, цифру в разряде сотых не меняем. Получим десятичную дробь 1,58.

– И осталось округлить нашу периодическую дробь до тысячных, – продолжил Паша. – Для округления нам необходимо отбросить все цифры, которые стоят после разряда тысячных. Первая из отбрасываемых цифр равна 3. Следовательно, цифру в разряде тысячных увеличивать не надо. Получим десятичную дробь 1,583.

– Молодцы! – похвалил ребят Мудряш. – Полученные числа 2; 1,6; 1,58 и 1,583 называют десятичным приближением до единиц, десятых, сотых и тысячных соответственно дроби . Записывают десятичные приближения так:

– Рассмотренный пример иллюстрируют следующее правило, – сказал Мудряш. – Запомните! Чтобы найти десятичное приближение обыкновенной дроби до нужного разряда, надо:

во-первых, выполнить деление до следующего разряда;

во-вторых, полученную конечную десятичную дробь или бесконечную периодическую десятичную дробь округлить до нужного разряда по обычным правилам округления. Если «отбрасываемый» разряд содержит цифры 0, 1, 2, 3, 4, то разряд, до которого округляют, не изменяют; если «отбрасываемый» разряд содержит цифры 5, 6, 7, 8, 9, то его отбрасывают, а разряд, до которого округляют, увеличивают на 1.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

Задание первое: найдите десятичное приближение до указанного разряда: а)  – до десятых;      б)  – до десятых;       в)  – до сотых;           г)  – до тысячных.

Решение: первая дробь — . Её по условию нужно округлить до десятых. Выполним деление уголком. Достаточно найти её значение до разряда сотых.

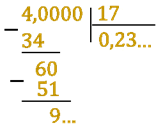
Получим десятичную дробь 0,23. А теперь округлим эту дробь до десятых. Для этого отбросим сотые. При этом отбрасываемая цифра равна 3, значит, цифру, стоящую в десятых, увеличивать не нужно. Получим десятичную дробь нуль 0,2.

Следующая дробь — . Её тоже нужно округлить до десятых. Выполним деление уголком числителя на знаменатель. Нам достаточно найти значение частного до разряда сотых.

Получим десятичную дробь 3,14. В разряде сотых стоит 4. Значит, округляемый разряд увеличивать не нужно. Получим дробь 3,1.

Перейдём к следующей дроби . Её нужно округлить до сотых. Разделим уголком четыре на тринадцать. Нам достаточно найти значение частного до разряда тысячных.

Получим десятичную дробь 0,307. Отбросим разряд тысячных. Так как после округляемой цифры стоит 7, то округляемый разряд увеличиваем на 1. Получим 0,31.

И последняя дробь — . Её нужно округлить до тысячных. Выполним деление уголком двух на три. Нам достаточно найти значение частного до разряда десятитысячных.

Получим десятичную дробь 0,6666. Отбросим разряд десятитысячных. Там стоит 6, значит, округляемый разряд нужно увеличить на 1. Получим 1,667.

Следующее задание: найдите корень уравнения с точностью до сотых: а) ;      б) .

Решение: первое уравнение . Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. Выполним деление уголком до разряда тысячных. Получим десятичную дробь 1,315. Результат нужно округлить до сотых. В разряде тысячных стоит 5. Значит, разряд сотых увеличим на 1. Тогда получим десятичную дробь 1,32.

Следующее уравнение . Чтобы найти делитель, нужно делимое разделить на частное. Выполним деление уголком до разряда тысячных. Получим десятичную дробь 0,122. Результат нужно округлить до сотых. В разряде тысячных стоит 2. Значит, разряд сотых не изменяем. Тогда получим десятичную дробь 0,12.

И последнее задание: площадь прямоугольника равна 2730 м², а длина одной из сторон этого прямоугольника равна 55 метрам. Найдите длину другой стороны прямоугольника. Ответ округлите до сотых метра.

Решение: мы знаем, что площадь прямоугольника равна произведению длин его соседних сторон. Выразим из этой формулы неизвестную сторону. Получим, что вторая сторона равна частному 2730 и 55. Выполним деление уголком до разряда тысячных. Получим десятичную дробь 49,633. В разряде тысячных стоит 6. Значит, разряд сотых увеличим на 1. Тогда получим, что вторая сторона 49,64 метра.