Представим себе такую историю…
– Саша, чем ты занимаешься? – поинтересовался у друга Паша.
– Хочу порадовать родителей и приготовить к обеду рисовую кашу, – ответил Саша.
– Отличная идея! – согласился Паша. – Так чего не варишь?
– В рецепте я прочитал, что объёмы крупы и воды при варке каши должны относиться как 1 к 2, – стал рассказывать Саша. – Но что это означает? К 1 крупинке риса нужно добавить 2 капельки воды что ли? Или к 1 пакету риса нужно добавлять 2 воды? И чем воду тогда измерять?
– Да тут всё просто! – улыбнулся Паша. – Отношение 1 к 2 говорит, что на один стакан крупы понадобится два стакана воды.
– Теперь понятно! – обрадовался Саша. – Одного стакана риса, конечно, будет маловато, чтобы накормить всех. Добавлю-ка я лучше 3 стакана риса и тогда нужно будет налить… так, так, так… 9 стаканов воды? Правильно?
– Нет, – сказал Паша. – Давай поразмышляем вместе. Смотри: если мы берём 1 стакан крупы и добавляем 2 стакана воды, то для 2 стаканов крупы понадобится 4 стакана воды, а значит, для 3 стаканов крупы – 6 стаканов воды.
– А! Вот оно как считается, – задумался Саша. – А если бы я хотел сварить 5 стаканов риса, нужно было бы так долго считать? Мама как-то всё быстрее высчитывает, когда варит нам кашу.

– Возможно, есть какой-то способ для быстрого решения таких задач, – предположил Паша. – Давай лучше спросим у Мудряша. Он точно будет знать.
– Ребята, прежде чем я расскажу вам, как решают подобного рода задачи, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!
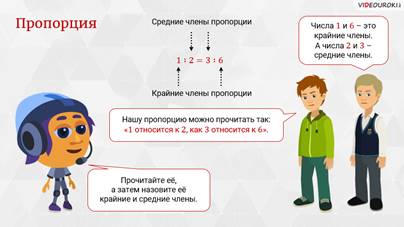
– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Давайте рассмотрим два отношения, которые у вас получились. Первое — 1 относится к 2, второе – 3 относится к 6. Обратите внимание: эти два отношения равны, так как значения частных равны 0,5. Поэтому мы можем записать, что отношение 1 к 2 равно отношению 3 к 6. Такое равенство называют пропорцией. Кстати, слово «пропорция» происходит от латинского корня и означает «соизмеримость».

– Запомните! – сказал Мудряш. – Равенство двух отношений называют пропорцией.
В
буквенном виде пропорцию можно записать так:  или так:
или так: 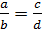 . Прочитать данные записи
можно следующим образом: «отношение
. Прочитать данные записи
можно следующим образом: «отношение 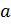 к
к 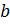 равно
отношению
равно
отношению 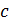 к
к 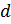 »,
или «
»,
или «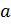 относится к
относится к 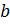 ,
как
,
как 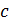 относится к
относится к 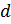 »,
или «число
»,
или «число 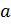 относится к числу
относится к числу 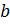 ,
как число цэ к числу дэ». Буквенная запись
пропорции
,
как число цэ к числу дэ». Буквенная запись
пропорции 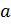 относится к
относится к 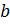 ,
как
,
как 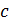 относится к
относится к 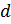 ,
– это общий вид пропорции, где
,
– это общий вид пропорции, где 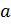 ,
, 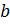 ,
,
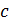 и
и 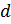 называют членами
пропорции, причём числа
называют членами
пропорции, причём числа 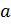 и
и 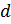 называют крайними
членами пропорции, а числа
называют крайними
членами пропорции, а числа 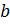 и
и 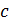 – средними
членами пропорции.
– средними
членами пропорции.

Эти названия условны – достаточно написать пропорцию в обратном порядке (слева направо), и крайние члены станут средними, а средние – крайними. Договариваются, что все члены пропорции отличны от нуля.
– Давайте вернёмся к нашей пропорции, – предложил Мудряш. — Прочитайте её, а затем назовите её крайние и средние члены.
– Нашу пропорцию можно прочитать так, – начал Саша, – «1 относится к 2, как 3 относится к 6».
– В нашей пропорции числа 1 и 6 – это крайние члены, – продолжил Паша. — А числа 2 и 3 – средние члены.
– Молодцы! – похвалил ребят Мудряш. – А теперь посмотрите на следующие два отношения. Скажите, могут ли они образовать пропорцию?
– Эти отношения не могут образовать пропорцию, – ответил Паша, – так как отношение 3 к 9 не равно отношению 5 к 25.

– А можно ли как-нибудь убедиться, что перед нами верная пропорция? – решили уточнить мальчишки.
– Хороший вопрос, – сказал Мудряш. – Вернёмся снова к вашей пропорции. Давайте попробуем найти произведения её крайних и средних членов.
– Произведение крайних членов пропорции равно 6, – посчитал Саша.
– Произведение средних членов тоже равно 6, – ответил Паша.

–
Видим, что эти произведения равны, – продолжил Мудряш. – Такое свойство присуще
любой верной пропорции. Запомните! Произведение крайних членов
пропорции равно произведению её средних членов. То есть выполняются следующие
равенства: если 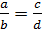 , то
, то 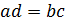 . Это свойство называют основным
свойством пропорции.
. Это свойство называют основным
свойством пропорции.
Верно
и обратное утверждение. Если произведение крайних членов пропорции равно
произведению средних членов, то пропорция 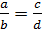 верна. Это свойство
называется признаком пропорции.
верна. Это свойство
называется признаком пропорции.
–
А теперь давайте выясним, применяя основное свойство пропорции, образуют ли
следующие отношения пропорции: 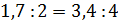 ,
, 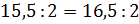 .
.
–
Чтобы установить, образуют ли отношения пропорцию, достаточно проверить, равны
ли произведения её крайних и средних членов, – начал размышлять Саша. – Произведение
крайних членов первой пропорции равно 6,8. Произведение средних членов равно 6,8.
То есть произведение крайних членов пропорции равно произведению средних
членов. Значит, равенство 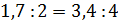 является пропорцией.
является пропорцией.
–
Найдём произведения крайних и средних членов второй пропорции, – продолжил
Паша. – Произведение крайних членов пропорции равно 31, а произведение средних
членов равно 33. Видим: произведение крайних членов пропорции не равно
произведению её средних членов. Следовательно, записанное равенство 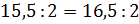 не
является пропорцией.
не
является пропорцией.

– Молодцы! – похвалил ребят Мудряш. – Обратите внимание: если в верной пропорции поменять местами крайние члены и средние члены, то получившиеся новые пропорции также верны.

– Ну а теперь давайте разберёмся, как можно было решить первоначальную задачу про кашу, что хотел Саша сварить на обед, – предложил Мудряш. – Итак, вам было известно, что на 1 стакан риса необходимо 2 стакана воды. То есть имеем отношение 1 к 2. Саша не мог определиться, сколько же тогда воды понадобится на 3 стакана риса. Давайте обозначим за х стаканы воды, что нужно вычислить. То есть имеем отношение 3 к х. Составим из этих отношений пропорцию.
–
Мне кажется я догадался, как можно было вычислить, сколько стаканов воды
понадобится на 3 стакана крупы, – сказал Саша. – По основному свойству
пропорции произведение крайних членов пропорции равно произведению её средних
членов. Тогда можем записать, что 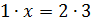 . Или
. Или 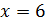 .
То есть на 3 стакана риса нужно 6 стаканов воды.
.
То есть на 3 стакана риса нужно 6 стаканов воды.

–
Всё правильно! – согласился Мудряш. – Если три члена пропорции известны, а
четвёртый нужно найти, то говорят, что это задача на пропорцию. Задачи на
пропорции возникают очень часто. Запомните! Чтобы найти неизвестный
крайний член пропорции, нужно произведение её средних членов разделить на
известный крайний член пропорции 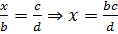 . Совершенно
аналогично формируется правило для нахождения неизвестного среднего члена
пропорции: чтобы найти неизвестный средний член пропорции, нужно
произведение её крайних членов разделить на известный средний член
. Совершенно
аналогично формируется правило для нахождения неизвестного среднего члена
пропорции: чтобы найти неизвестный средний член пропорции, нужно
произведение её крайних членов разделить на известный средний член 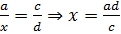 .
.
– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание
первое: составьте пропорции из чисел: а) 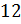 ;
;
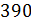 ;
; 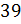 ;
;
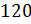 ; б)
; б) 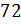 ;
;
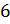 ;
; 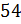 ;
;
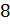 ; в)
; в) 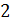 ;
;
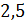 ;
; 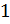 ;
;
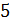 ; г)
; г) 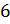 ;
;
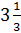 ;
; 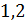 ;
;
 .
.
Решение: первая
четвёрка чисел: 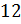 ;
; 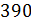 ;
;
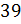 ;
; 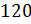 .
Не сложно заметить, что из этих чисел можно составить следующую пропорцию:
.
Не сложно заметить, что из этих чисел можно составить следующую пропорцию: 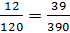 .
.
Следующая
четвёрка чисел: 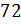 ;
; 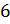 ;
;
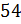 ;
; 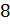 .
Из данных чисел можно составить такую пропорцию:
.
Из данных чисел можно составить такую пропорцию: 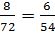 .
.
Перейдём
к следующей четвёрке чисел: 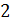 ;
; 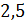 ;
;
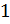 ;
; 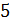 .
Понятно, что из этих чисел можно составить такую пропорцию:
.
Понятно, что из этих чисел можно составить такую пропорцию: 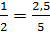 .
.
И
последняя четвёрка чисел: 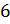 ;
; 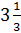 ;
; 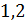 ;
;
 . Для удобства представим
смешанное
. Для удобства представим
смешанное 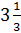 в виде неправильной
дроби
в виде неправильной
дроби 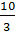 , а десятичную дробь 1,2
сначала запишем смешанным числом
, а десятичную дробь 1,2
сначала запишем смешанным числом 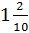 , затем сократим дробную
часть на 2 и потом представим смешанное число
, затем сократим дробную
часть на 2 и потом представим смешанное число 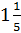 в виде неправильной
дроби
в виде неправильной
дроби  . Тогда из указанных
чисел можно составить следующую пропорцию:
. Тогда из указанных
чисел можно составить следующую пропорцию: 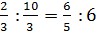 , или
, или 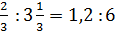 .
.

Следующее
задание: являются ли данные пропорции верными: а) 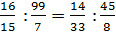 ; б)
; б) 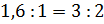 ?
?
Решение: чтобы
ответить на вопрос, являются ли пропорции верными, достаточно проверить, равны
ли произведения крайних и средних членов пропорций. Произведение крайних членов
первой пропорции равно 6. Произведение средних членов равно 6. То есть
произведение крайних членов пропорции равно произведению средних членов.
Значит, равенство 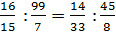 является пропорцией.
является пропорцией.
Найдём
произведения крайних и средних членов второй пропорции 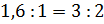 .
Произведение крайних членов пропорции равно 3,2, а произведение средних членов
равно 3. Видим: произведение крайних членов пропорции не равно произведению её
средних членов. Следовательно, записанное равенство
.
Произведение крайних членов пропорции равно 3,2, а произведение средних членов
равно 3. Видим: произведение крайних членов пропорции не равно произведению её
средних членов. Следовательно, записанное равенство 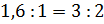 не
является пропорцией.
не
является пропорцией.

И решим задачу: на территории России имеется более 130 000 рек длиной от 10 километров и больше. Известно, что каждый год человек загрязняет 2 % этих рек. Сколько рек загрязняет человек каждый год?
Решение:
пусть х рек загрязняет человек каждый год. Возьмём все реки длиной более
10 километров, то есть 130 000 рек за 100 %. Тогда можем переписать условие
нашей задачи следующим образом: 130 000 рек – это 100 %, х рек – это 2 %.
Отношения 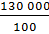 и
и  равны, поскольку каждое
из них показывает, сколько рек составляют 1 %. Значит, из этих отношений мы
можем составить пропорцию. Мы знаем, что для того, чтобы найти неизвестный
средний член пропорции, нужно произведение её крайних членов разделить на
известный средний член. Посчитаем и получим, что за год человек загрязняет 2600
рек.
равны, поскольку каждое
из них показывает, сколько рек составляют 1 %. Значит, из этих отношений мы
можем составить пропорцию. Мы знаем, что для того, чтобы найти неизвестный
средний член пропорции, нужно произведение её крайних членов разделить на
известный средний член. Посчитаем и получим, что за год человек загрязняет 2600
рек.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 3652
3652


