Представим себе такую историю…
– Саша, ты что такой задумчивый сидишь? – спросил у друга Паша.
– На каникулы нам задали прочитать книгу, которая состоит из 300 страниц, – начал рассказывать Саша. – Я уже прочитал 75 страниц. Вот мне стало интересно, сколько же процентов книги я уже прочитал.
– Давай попробуем вместе посчитать, – предложил Паша. – Ты сказал, что книга состоит из 300 страниц. Значит, эти страницы будут составлять 100 %.
– Ну да… – согласился Саша. – И как же это поможет выяснить, сколько процентов составляют прочитанные 75 страниц?
– 150 страниц — это половина книги, – продолжил Паша, – значит, 150 страниц будут составлять 50 %. А вот твои 75 страниц – это четверть книги. Следовательно, 75 страниц будут составлять 25 %.
– Ух ты! Как ты лихо всё посчитал, – воскликнул Саша. – А если бы я прочитал не 75 страниц, а, например, 73? То как бы тогда считать надо было?

– Не знаю, – задумался Паша. – Давай лучше спросим у Мудряша, как решают подобные задачи. Он уж точно сможет объяснить.
– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!
– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Задачи такого рода удобно решать с помощью пропорций. Чтобы ответить на вопрос «Сколько процентов составляют прочитанные Сашей страницы от страниц всей книги?», нужно найти процентное отношение. Сейчас я вам объясню, как его находят. Вы уже умеете находить часть от целого. Скажите, какую часть составляют страницы, прочитанные Сашей, от страниц всей книги?
–
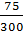 ,
– посчитал Саша.
,
– посчитал Саша.
–
Можем сократить эту дробь на 75, – заметил Паша. – Тогда прочитанные Сашей
страницы составляют  часть
от страниц всей книги.
часть
от страниц всей книги.
– Верно, – согласился Мудряш. – А теперь выразите это отношение в процентах.
–
Умножим дробь  на
100, – сказал Паша. – Получится 25 %. И у меня в вычислениях тоже получилось 25
%.
на
100, – сказал Паша. – Получится 25 %. И у меня в вычислениях тоже получилось 25
%.
– Число 25 показывает, сколько процентов страниц в книге составляют прочитанные Сашей страницы, – заметил Мудряш. – Это число называют процентным отношением.

Запомните! Процентное отношение двух чисел – это их отношение, выраженное в процентах. Процентное отношение показывает, сколько процентов одно число составляет от другого.
– Давайте рассмотрим ещё один пример, – предложил Мудряш. – Вот скажите, сколько мальчиков и сколько девочек учатся в вашем классе?
– В нашем классе учатся 10 девочек и 15 мальчиков, – ответили мальчишки.
– Давайте рассчитаем процентное отношение количества девочек к количеству мальчиков; процентное отношение количества мальчиков к количеству девочек; процентное отношение количества девочек к количеству учащихся всего класса и процентное отношение количества мальчиков к количеству учащихся всего класса, – сказал Мудряш.
–
Процентное отношение количества девочек к количеству мальчиков равно 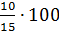 и
равно
и
равно 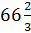 %,
– посчитал Саша. – Это отношение показывает, что количество девочек составляет
%,
– посчитал Саша. – Это отношение показывает, что количество девочек составляет 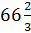 %
от количества мальчиков.
%
от количества мальчиков.
–
Число 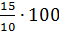 и
равное 150 % показывает, что количество мальчиков составляет 150 % от
количества девочек, – продолжил Паша.
и
равное 150 % показывает, что количество мальчиков составляет 150 % от
количества девочек, – продолжил Паша.
–
Так как в классе учатся 10 девочек и 15 мальчиков, то всего в классе 25 учеников,
– сказал Саша. – следовательно, процентное отношение количества девочек к
количеству учащихся всего класса равно 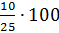 и
равно 40 %.
и
равно 40 %.
–
Число 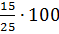 и
равное 60 % показывает, что количество мальчиков составляет 60 % от количества
всех учащихся в классе, – продолжил Паша.
и
равное 60 % показывает, что количество мальчиков составляет 60 % от количества
всех учащихся в классе, – продолжил Паша.

– Молодцы! – похвалил ребят Мудряш. – Можем сделать следующий вывод. Запомните! Чтобы найти процентное отношение двух чисел, надо их отношение умножить на сто и к результату дописать знак процента.
Кстати, при решении задач на процентное отношение, кроме этого правила, можно использовать пропорции.
– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание
первое: сколько процентов число 20 составляет от указанных
чисел: а) 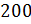 ;
б)
;
б) 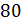 ;
в)
;
в) 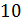 ;
г)
;
г) 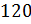 ?
?
Решение: чтобы
найти процентное отношение двух чисел, надо их отношение умножить на сто и к
результату дописать знак процента. Найдём процентное отношение числа 20 от
числа 200. 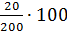 .
Получим 10 %.
.
Получим 10 %.
Затем
найдём процентное отношение числа 20 от числа 80. Для этого отношение 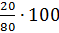 .
Получим 25 %.
.
Получим 25 %.
Дальше
найдём процентное отношение числа 20 от числа 10. Отношение 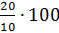 .
Получим 200 %.
.
Получим 200 %.
И
осталось вычислить процентное отношение числа 20 от числа 120. Число 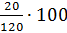 .
Получим
.
Получим 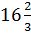 %.
%.

Следующее
задание: сколько процентов составляет одно число от другого: а)
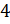 от
от
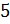 ;
б)
;
б) 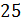 от
от
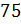 ;
в)
;
в) 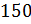 от
от
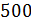 ;
г)
;
г) 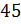 от
от
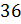 ?
?
Решение:
чтобы
найти процентное отношение двух чисел, надо их отношение умножить на сто и к
результату дописать знак процента. Тогда процентное
отношение числа 4 от числа 5 равно 80 %. Процентное отношение числа 25 от 75
равно 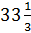 %.
Процентное отношение числа 150 от числа 500 равно 30 %. А процентное отношение
числа 45 от числа 36 равно 125 %.
%.
Процентное отношение числа 150 от числа 500 равно 30 %. А процентное отношение
числа 45 от числа 36 равно 125 %.

А теперь давайте решим несколько задач.
Задача первая: в школе 800 учеников, 48 из них — отличники. Какой процент всех учащихся в школе составляют отличники?
Решение: пусть
отличники составляют х %. Тогда можем записать, что 800 учеников – это 100
%, а 48 учеников-отличников – это х %. Отношения 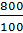 и
и
 равны,
поскольку каждое из них показывает, сколько учеников приходится на 1 %. Имеем
пропорцию:
равны,
поскольку каждое из них показывает, сколько учеников приходится на 1 %. Имеем
пропорцию: 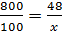 .
Чтобы найти неизвестный крайний член пропорции, нужно произведение её
средних членов разделить на известный крайний член пропорции. Отсюда
.
Чтобы найти неизвестный крайний член пропорции, нужно произведение её
средних членов разделить на известный крайний член пропорции. Отсюда 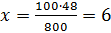 .
То есть 6 % всех учащихся в школе составляют отличники.
.
То есть 6 % всех учащихся в школе составляют отличники.

Задача вторая: норма завода по производству автомобилей составляет 250 машин в месяц. Завод собрал за месяц 315 машин. На сколько процентов завод перевыполнил план?
Решение:
для начала найдём процентное отношение количества собранных автомобилей к
количеству автомобилей, установленных нормой. Получим 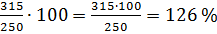 .
Так как норма по сбору автомобилей составляет 100 %, а завод за месяц собрал 126
% нормы автомобилей, то завод перевыполнил план на 26 %. Не забудем записать
ответ.
.
Так как норма по сбору автомобилей составляет 100 %, а завод за месяц собрал 126
% нормы автомобилей, то завод перевыполнил план на 26 %. Не забудем записать
ответ.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 5906
5906

