Прямая и обратная пропорциональные зависимости

Представим себе такую историю…

– Саша, чем ты занимаешься? – поинтересовался Паша.

– Нам по математике задали разгадать ребус, по которому мы узнаем тему нашего следующего урока, – ответил Саша. — А в этом ребусе как-то чересчур всё запутанно.

– Не расстраивайся! – подбодрил друга Паша. – Я помогу тебе. Показывай свой ребус.

– Вот, смотри, какое длиннющее слово! – воскликнул Саша.

– Саша, да это совсем лёгкий ребус, – возразил Паша. – Сейчас мы вместе быстренько всё разгадаем. Итак, твой ребус начинается с буквы «п». Букву эту и оставим на первом месте. Затем нарисован топор, а под ним равенство цифры и буквы. Знак равенства, изображённый возле картинки, служит для обозначения замены одной из букв на другую. У тебя нарисован топор, а снизу равенство, указывающее, что нужно первую букву в названии картинки заменить на букву «р». Что за слово получится после замены?

– Был топор, заменим первую букву на «р», значит, у нас получится «ропор», – сказал Саша.

– Верно! – согласился Паша. – Перейдём к следующей картинке. Напомню, что запятые в ребусе означают, что из названия картинки нужно исключить столько букв, сколько стоит запятых. Если запятые стоят перед картинкой, то убираем буквы в начале слова, если после – в конце слова, – вспомнил Паша. – После нашей картинки стоят две запятые. Что за слово получится?

– У нас нарисован цирк, – начал размышлять Саша. – А после картинки стоят две запятые. Значит, исключим последние две буквы. И останется у нас «ци».

– Отлично! – поддержал друга Паша. – Идём дальше. Если один предмет или символ нарисован под другим, то слово расшифровываем с прибавлением предлога «над», «на» или «под». Предлог нужно выбрать по смыслу. Попробуй расшифровать.

– Так, – стал размышлять Саша, – здесь написаны две буквы, причём буква «о» написана над буквой «эль». Значит, может получиться либо «О над ЭЛЬ», либо «О на ЭЛЬ», либо «ЭЛЬ под О».

– Хорошо! – согласился Паша. – Перейдём к следующей картинке. Если картинка перевёрнута вверх ногами, это значит, что слово читается задом наперёд. Плюс у нас тут ещё написано равенство цифры и буквы, которое указывает, что четвёртую букву в слове нужно заменить на «с». Что тогда получится?

– У нас нарисован конь, – начал размышлять Саша. – Задом наперёд это слово читается так: «ЬНОК». Затем заменим четвёртую букву на «с». И получится у нас «ЬНОС».

– Верно! – согласился Паша. – Перейдём к последней картинке. Не забудь, перед нашей картинкой стоят три запятые. Что за слово получится?

– У нас нарисована кисть, – сказал Саша. – Перед картинкой стоят три запятые. Значит, исключим первые три буквы. И останется у нас «ть».

– Молодец! – обрадовался за друга Паша. – А теперь попробуй из получившихся слогов и букв составить единое слово.

– Так, – начал Саша, – у нас есть буква «п», слово «ропор», слог «ци», затем нужно выбрать один из вариантов «О над ЭЛЬ», «О на ЭЛЬ», «ЭЛЬ под О», потом идёт слово «ЬНОС» и слог «ть». Подумаем… Так это же «пропорциональность»!

– Молодец, Саша! – похвалил друга Паша. — Значит, на уроке математики вы будете знакомиться с пропорциональностью!

– Интересно, что это за пропорциональность такая? – спросил Саша.

– А давай спросим у Мудряша, – предложил Паша. – Он точно сможет объяснить.

– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Часто в жизни мы сталкиваемся с различными величинами – это главный инструмент описания окружающего мира. Величиной называют такое свойство предмета или объекта, которое можно измерить. Например, возраст дерева, высота дома, скорость передвижения. Величины могут быть связаны, зависеть друг от друга или нет.

– Давайте рассмотрим такой пример – предложил Мудряш. – 1 килограмм яблок стоит 50 рублей. Сколько рублей нужно отдать за 3 килограмма яблок?

– Ну что тут считать, – улыбнулся Саша, – так как 1 килограмм яблок стоит 50 рублей, то за 3 килограмма яблок придётся заплатить 150 рублей.

– Хорошо! – согласился Мудряш. – Тогда скажите, а сколько нужно будет заплатить, например, за 6 килограмм яблок?

– И тут несложно посчитать, – сказал Паша. – За 6 килограмм яблок придётся заплатить 300 рублей.

– Молодцы! – похвалил ребят Мудряш. – Посмотрите на таблицу. Здесь указана зависимость стоимости покупки от количества килограммов яблок. Что вы можете сказать об этой зависимости?

– Понятно, что стоимость товара напрямую зависит от его количества, – заметил Паша. – Чем больше товара покупают, тем больше будет его стоимость.

– Если нужно купить 2 килограмма яблок, то и стоимость покупки увеличится в 2 раза, – продолжил Саша, – если же необходимо купить 3 килограмма яблок, стоимость покупки также увеличится, но уже в 3 раза и так далее.

– Правильно! – сказал Мудряш. – Из таблицы видно, что увеличение (уменьшение) количества килограммов яблок в несколько раз приводит к соответствующему увеличению (уменьшению) стоимости покупки.

Запомните! Две переменные величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.

– Вернёмся к нашему примеру, – продолжил Мудряш, – количество и стоимость – это прямо пропорциональные величины. Также можно сказать, что стоимость прямо пропорциональна количеству или зависимость между количеством и стоимостью является прямой пропорциональностью.

– Давайте найдём отношения стоимости покупки к количеству, – сказал Мудряш.

– Отношения стоимости покупки к количеству будут равны, – начал Саша, – , , , ,  и .

– Ой, так все эти отношения равны, – заметил Паша. – Если мы вычислим значения этих отношений, то увидим, что все они равны 50.

– Молодцы! – похвалил ребят Мудряш. – Эти равенства иллюстрируют свойство переменных величин, которые находятся в прямой пропорциональной зависимости. Запомните! Если две переменные величины прямо пропорциональны, то отношение соответствующих значений этих величин равно одному и тому же, постоянному для данных величин, числу.

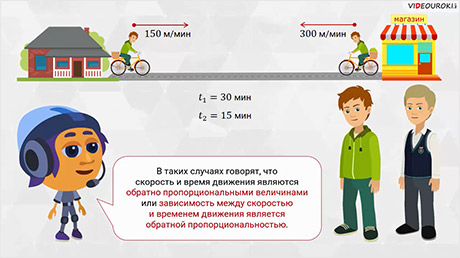
– Однако не всякая зависимость между переменными величинами является прямой пропорциональностью, – продолжил Мудряш. – Давайте рассмотрим пример из вашей жизни. Представим, что Саша поехал в магазин на велосипеде. Расстояние от дома до магазина Саша проехал за 30 минут, двигаясь со скоростью 150 метров в минуту, а на обратную дорогу затратил всего лишь 15 минут, двигаясь со скоростью 300 метров в минуту.

– Что вы можете сказать о Сашиной поездке в магазин? – спросил у ребят Мудряш.

– На обратном пути Саша увеличил скорость в 2 раза и потратил на дорогу в 2 раза меньше времени.

– Правильно! – согласился Мудряш. – Увеличение скорости в 2 раза привело к уменьшению затраченного времени также в 2 раза. Несложно догадаться, что если бы Саша увеличил скорость в 3 раза, в 4 раза, в 5 раз и так далее, то время движения уменьшилось бы соответственно в 3 раза, в 4 раза, в 5 раз. И наоборот, если бы Саша уменьшил скорость движения в несколько раз, то во столько же раз увеличилось бы время движения. В таких случаях говорят, что скорость и время движения являются обратно пропорциональными величинами или зависимость между скоростью и временем движения является обратной пропорциональностью.

– Запомните! – продолжил Мудряш. – Две переменные величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из этих величин в несколько раз другая уменьшается (увеличивается) во столько же раз.

– И снова вернёмся к нашему примеру, – сказал Мудряш. – Мы с вами убедились: при увеличении Сашей скорости в 2 раза время на дорогу уменьшилось тоже в 2 раза. Но обратите внимание: расстояние, которое Саша проехал от дома до магазина и из магазина домой, не поменялось. Этот пример иллюстрирует свойство переменных величин, которые находятся в обратно пропорциональной зависимости.

Запомните! Если две переменные величины обратно пропорциональны, то произведение соответствующих значений этих величин равно одному и тому же для данных величин числу.

– Важно понимать, что не всякие две величины являются прямо пропорциональными или обратно пропорциональными. Например, возраст человека и размер его обуви не связаны пропорциональной зависимостью. Понятно, что зависимость между величинами есть. Размер обуви с возрастом, конечно, увеличивается, но не во столько же раз.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

Задача первая: для приготовления борща на каждые 100 грамм мяса надо взять 60 грамм свёклы. Сколько свёклы надо взять на 650 грамм мяса?

Решение: это задача на прямую пропорциональную зависимость, так как чем больше в борщ будут добавлять мяса, тем больше потребуется свёклы. Для наглядности запишем краткое условие задачи, обозначим за х неизвестную нам массу свёклы. Масса мяса увеличилась, поставим стрелку от меньшего к большему, но и масса свёклы тоже увеличилась, значит, тоже поставим стрелку от меньшего к большему. Составим пропорцию: . Найдём неизвестный крайний член пропорции. Тогда на 650 грамм мяса нужно взять 390 грамм свёклы. Не забудем записать ответ.

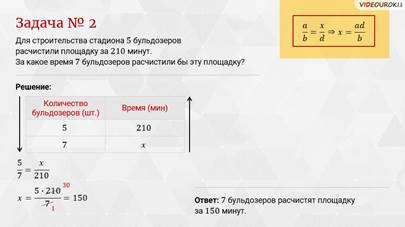
Задача вторая: для строительства стадиона 5 бульдозеров расчистили площадку за 210 минут. За какое время 7 бульдозеров расчистили бы эту площадку?

Решение: это задача на обратно пропорциональную зависимость, так как с увеличением количества бульдозеров время на расчистку стадиона уменьшится. Для наглядности запишем краткое условие задачи, обозначим за х неизвестное нам время. Количество бульдозеров увеличилось, поставим стрелку от меньшего к большему, а вот время на расчистку стадиона уменьшилось, поставим стрелку в обратном направлении. Составим пропорцию . Обратите внимание: члены второго отношения мы поменяли местами, чтобы не нарушить свойство пропорции. Найдём неизвестный средний член пропорции. Тогда получим, что 7 бульдозеров расчистят площадку за 150 минут. Запишем ответ.