
«ЗОЛОТОЕ СЕЧЕНИЕ» В ЖИВОПИСИ, ПРИРОДЕ И АРХИТЕКТУРЕ Г. АСТРАХАНЬ

Цели :
- Изучение принципа «золотого сечения» или «божественной пропорции».
- Изучение истории принципа «золотого сечения».
- Рассмотрение примеров применения принципа «золотого сечения» в различных областях человеческой деятельности и культуры.
- Выполнение практических заданий на пропорции и отношения и их анализ.

Целью проекта является выработка понимания, что математика – инструмент познания окружающего мира и самого себя.
Основные задачи:
- развитие интуиции и творческих способностей;
- совершенствование математической культуры и мировоззрения посредством изучения материала, связанного с историей возникновения и развития основных понятий, идей и методов.

«Геометрия обладает двумя
великими сокровищами.
Первое - это теорема Пифагора,
Второе - деление отрезка в крайнем
и среднем отношении».

Известные мыслители, ученые, изучавшие принципы «золотого сечения»
Аристотель
Евклид
Платон
ПИФАГОР Самосский
Лука Пачоли
Эйнштейн
Леонардо да Винчи
Иоган Кеплер

1,6180339887...
Области применения принципа «Золотого сечения»


- В математике пропорцией (лат. proportio) называют равенство двух отношений: a : b = c : d .
Определение «Золотого сечения»
- Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему
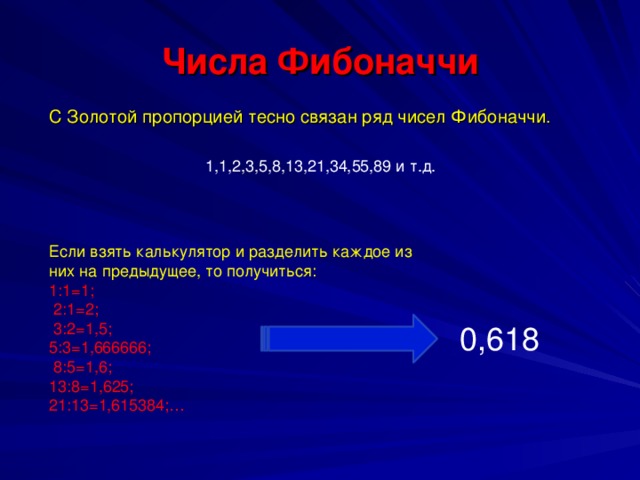
Числа Фибоначчи
С Золотой пропорцией тесно связан ряд чисел Фибоначчи.
1,1,2,3,5,8,13,21,34,55,89 и т.д.
Если взять калькулятор и разделить каждое из них на предыдущее, то получиться:
1:1=1;
2:1=2;
3:2=1,5;
5:3=1,666666;
8:5=1,6;
13:8=1,625;
21:13=1,615384;…
0,618
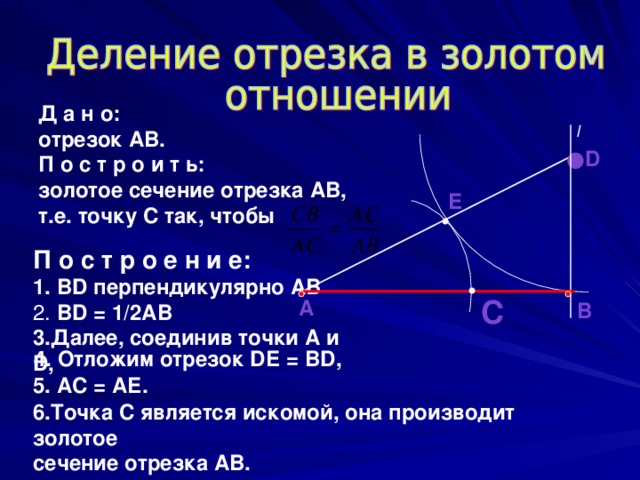
Д а н о:
отрезок АВ.
П о с т р о и т ь:
золотое сечение отрезка АВ, т.е. точку С так, чтобы
l
● D
Е
П о с т р о е н и е:
2. BD = 1/2АВ
C
А
В
3.Далее, соединив точки А и D,
4. Отложим отрезок DЕ = ВD,
5. АС = АЕ.
6.Точка С является искомой, она производит золотое
сечение отрезка АВ.
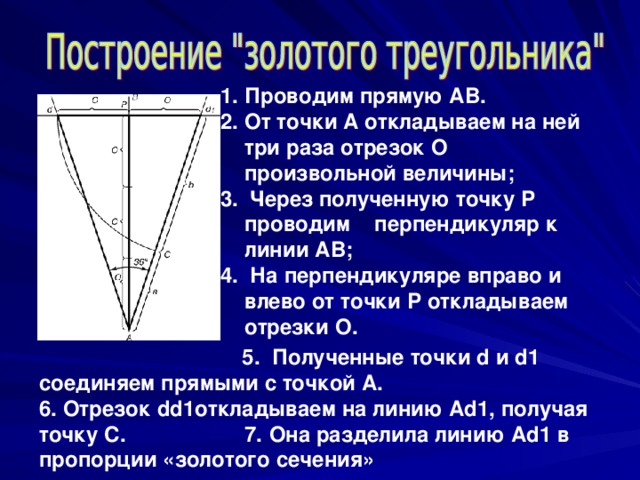
- Проводим прямую АВ.
- От точки А откладываем на ней три раза отрезок О произвольной величины;
3. Через полученную точку Р проводим перпендикуляр к линии АВ;
4. На перпендикуляре вправо и влево от точки Р откладываем отрезки О.
5. Полученные точки d и d1
соединяем прямыми с точкой А.
6. Отрезок dd1откладываем на линию Ad1, получая точку С. 7. Она разделила линию Ad1 в пропорции «золотого сечения»

«ЗОЛОТОЙ» ПРЯМОУГОЛЬНИК
Прямоугольник АЕFD со сторонами АЕ=φАD называется золотым прямоугольником. Четырехугольник АВСD - квадрат. Нетрудно видеть, что прямоугольник ВЕFС также золотой, поскольку BC=a=φВЕ . Это обстоятельство сразу наводит на мысль о дальнейшем разбиении прямоугольника ВЕFС .
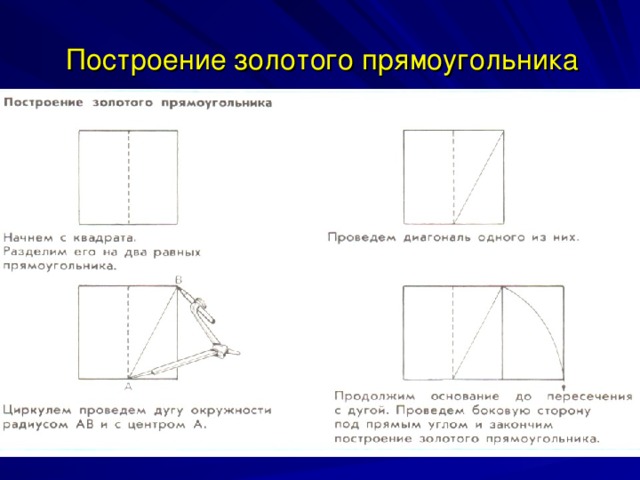
Построение золотого прямоугольника

«Золотой» пятиугольник
Замечательный пример «золотого сечения» представляет собой правильный пятиугольник – выпуклый и звездчатый
Все диагонали пятиугольника делят друг друга на отрезки, связанные между собой золотой пропорцией. Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны образуют угол 36° при вершине, а основание, отложенное на боковую сторону, делит ее в пропорции золотого сечения.

Золотое сечение в архитектуре древней Греции
Одним из красивейших произведений древнегреческой архитектуры является Парфенон (V в. до н.э .).
Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. выступы сделаны целиком из квадратов пентилейского мрамора.
Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон (синий и красный) для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по “золотому сечению”, то получим те или иные выступы фасада.

Золотое сечение в архитектуре древнего Рима
Другим примером из архитектуры является Пантеон – вершина древнеримского строительного искусства – храм всех богов.
В «классе каменных куполов» 43-метровый купол Пантеона в истории зодчества остался недосягаемым. Но Пантеон не только вершина научных и технических достижений древнеримских строителей, а и шедевр архитектурного искусства. В интерьере Пантеона достигнута завораживающая гармония между высотой и диаметром сооружения, которая имеет простое математическое выражение: высота стен Пантеона равна радиусу полусферы его купола, т.е. весь Пантеон как бы наброшен на 43 метровый шар.

Джоконда
Найдите на картине «золотой треугольник»


Портрет Моны Лизы привлекает тем, что композиция рисунка построена на"золотых треугольниках" (точнее на треугольниках, являющихся кусками правильного звездчатого пятиугольника).

«Золотое сечение» в природе
Выяснилось, что в расположении листьев на ветке, семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения.
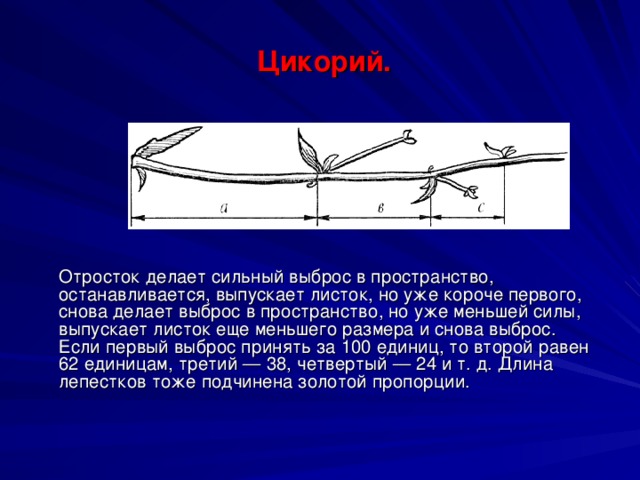
Цикорий.
Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий — 38, четвертый — 24 и т. д. Длина лепестков тоже подчинена золотой пропорции.
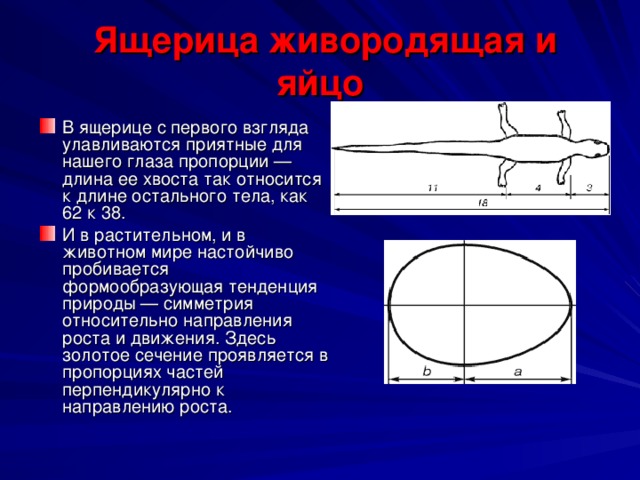
Ящерица живородящая и яйцо
- В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции — длина ее хвоста так относится к длине остального тела, как 62 к 38.
- И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы — симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.

Рассматривая расположение листьев на общем стебле, растений можно заметить, что между двумя парами листьев (А и С) Третья расположена в месте золотого сечения (в точке В)

Эксперимент
АВ=1,5
ВС=2,5
АС=4
АВ/ВС=0,6
ВС/АС=0,625
Φ =0,618
Герань
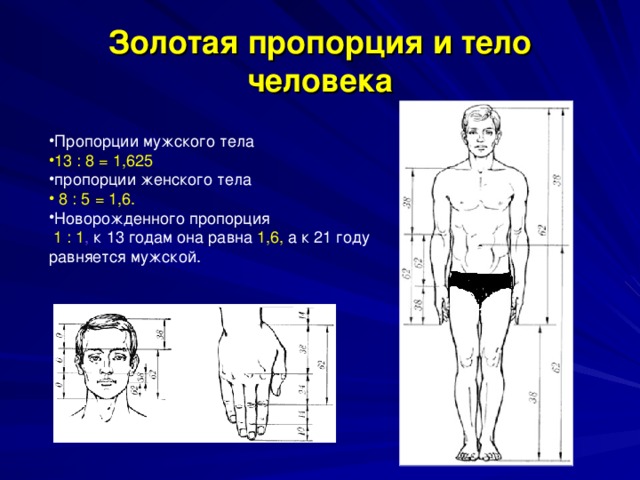
Золотая пропорция и тело человека
1 : 1 , к 13 годам она равна 1,6, а к 21 году равняется мужской.
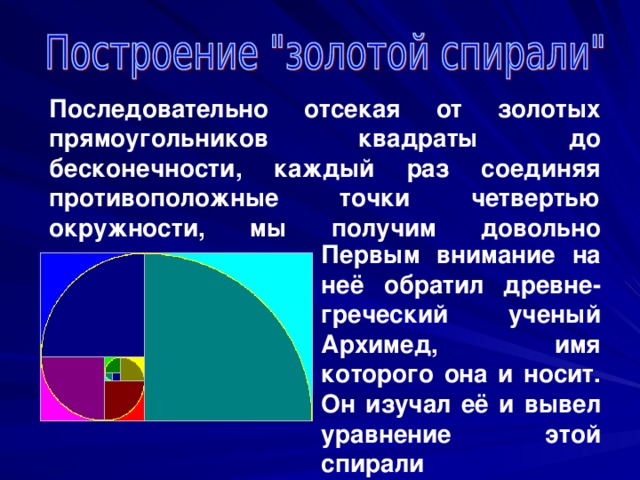
Последовательно отсекая от золотых прямоугольников квадраты до бесконечности, каждый раз соединяя противоположные точки четвертью окружности, мы получим довольно изящную кривую.
Первым внимание на неё обратил древне-греческий ученый Архимед, имя которого она и носит. Он изучал её и вывел уравнение этой спирали

Очень многие явления в природе описываются именно золотой спиралью. Расположение космических галактик, семян в шишке, завитков в раковине и многого другого подчинено закону золотой спирали. «Вечность времени и световые годы космоса разделяют сосновую шишку и спиральную галактику, но строение остается тем же самым: коэффициент 1,618, возможно, первостепенный закон, управляющий активными природными явлениями. Таким образом, золотая спираль развертывается перед нами в символической форме, как один из величественных замыслов природы, образ жизни в бесконечном расширении и сжатии, статический закон, управляющий динамическим процессом, подкрепленный и изнутри и снаружи пропорцией 1,618, золотым сечением».

Другой пример композиции рисунка - картина Дега «Танцовщицы». Динамика танца и его гармония здесь подчеркнуты «вихрем» танца, выраженным спиралью



Больница предприятия «Газпром» и банк «Траст»

Дом Тетюшинова и Астраханский кремль

Дом Воробьева и дом Губина

Дом Шелгунова

Заключение
Принцип золотого сечения – высшее проявление структурного совершенства целого и его частей в природе, искусстве, науке и технике

Список использованной литературы:
1. Волошинов А.В. Математика и искусство.-М.: Просвещение, 1992
2. Левитин К. Геометрическая рапсодия.- М.: Знание, 1984
3. Шевелев И.Ш. Принцип пропорции.- М.: Стройиздат, 1986
4. Шевелев И.Ш., Марутаев М.А. Золотое сечение.- М.: Стройиздат, 1990
5. Рощевская Л.П. Архитектура и строительство.


 Получите свидетельство
Получите свидетельство Вход
Вход
















































 Золотое сечение в природе, архитектуре и живописи (6.38 MB)
Золотое сечение в природе, архитектуре и живописи (6.38 MB)
 0
0 1634
1634 108
108 Нравится
0
Нравится
0


