Задачи на теорию вероятностей

Элементы теории вероятностей

Теория   вероятностей  — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними. 

Вероятность  — это степень возможности, что какое-то событие произойдет.

«

Метод «дерева»

Дерево  решений - это  метод , который применяется для принятия решений в условиях неопределенности и риска.

М етод  дерева - это схематичное изображение процесса принятия последовательных решений и состоит из ветвей – вариантов решения и узлов- соответствующих им исходов.

«

1 ф

2 ф

0.45

0.55

кач.

брак

брак

кач.

0.03

0.97

0.99

0.01

Задача 1

Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 45% этих стёкол. Первая фабрика выпускает 3 % бракованных стёкол, а вторая — 1 %. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Решение: вторая фабрика выпускает 100% - 45% = 55%

Строим дерево, у нас 2 ветви. И у каждой ветви есть по 2 ветви: качественные (кач) и бракованные (брак). Нас интересуют бракованные изделия, поэтому, смотрим на красные линии. Эти числа перемножаем отдельно в каждой ветви и результаты надо сложить. (Проценты записываем в виде десятичных дробей)

+

0.45 * 0.03

0.55 * 0.01

= 0.019

бел

чер

0.52

0.3

бел

чер

0.3

0.52

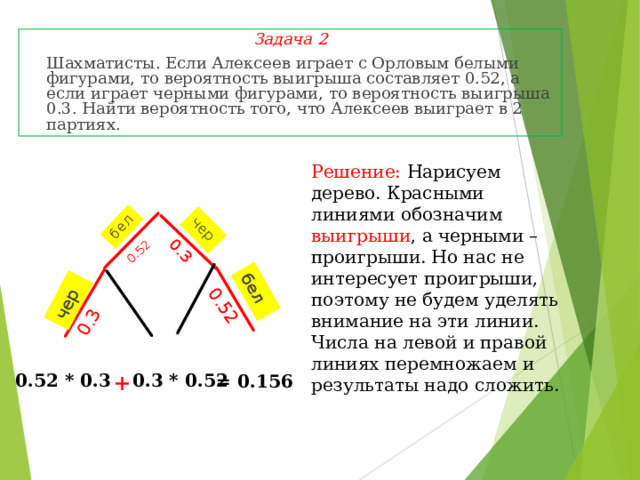
Задача 2

Шахматисты. Если Алексеев играет с Орловым белыми фигурами, то вероятность выигрыша составляет 0.52, а если играет черными фигурами, то вероятность выигрыша 0.3. Найти вероятность того, что Алексеев выиграет в 2 партиях.

Решение: Нарисуем дерево. Красными линиями обозначим выигрыши , а черными – проигрыши. Но нас не интересует проигрыши, поэтому не будем уделять внимание на эти линии. Числа на левой и правой линиях перемножаем и результаты надо сложить.

+

0.52 * 0.3

0.3 * 0.52

= 0.156

П

М

П

0.8

П

М

М

0.8

0.2

П

М

М

П

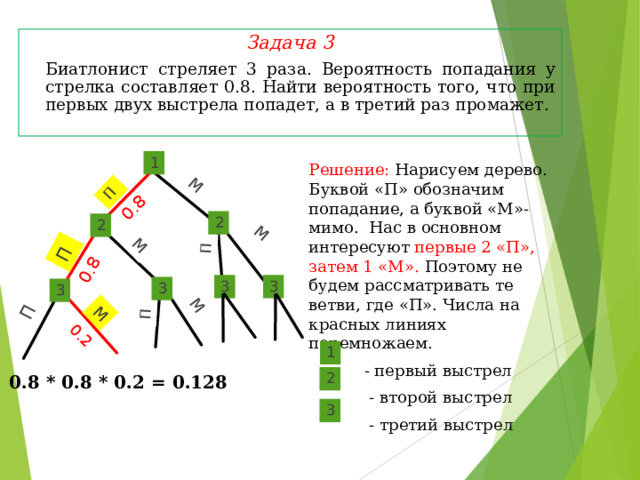
Задача 3

Биатлонист стреляет 3 раза. Вероятность попадания у стрелка составляет 0.8. Найти вероятность того, что при первых двух выстрела попадет, а в третий раз промажет.

1

Решение: Нарисуем дерево. Буквой «П» обозначим попадание, а буквой «М»- мимо. Нас в основном интересуют первые 2 «П», затем 1 «М». Поэтому не будем рассматривать те ветви, где «П». Числа на красных линиях перемножаем.

- первый выстрел

- второй выстрел

- третий выстрел

2

2

3

3

3

3

1

0.8 * 0.8 * 0.2 = 0.128

2

3

П

М

П

П

М

М

0.8

П

М

М

П

П

0.8

0.8

0.2

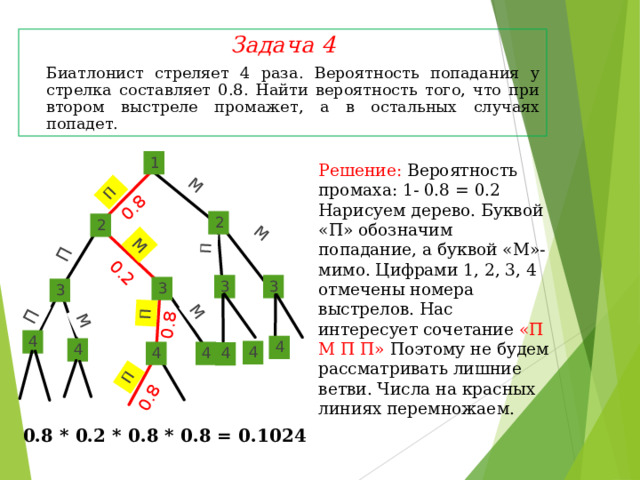
Задача 4

Биатлонист стреляет 4 раза. Вероятность попадания у стрелка составляет 0.8. Найти вероятность того, что при втором выстреле промажет, а в остальных случаях попадет.

1

Решение: Вероятность промаха: 1- 0.8 = 0.2 Нарисуем дерево. Буквой «П» обозначим попадание, а буквой «М»- мимо. Цифрами 1, 2, 3, 4 отмечены номера выстрелов. Нас интересует сочетание «П М П П» Поэтому не будем рассматривать лишние ветви. Числа на красных линиях перемножаем.

2

2

3

3

3

3

4

4

4

4

4

4

4

0.8 * 0.2 * 0.8 * 0.8 = 0.1024

П

М

П

П

М

М

0.8

П

М

М

П

П

0.8

0.8

0.2

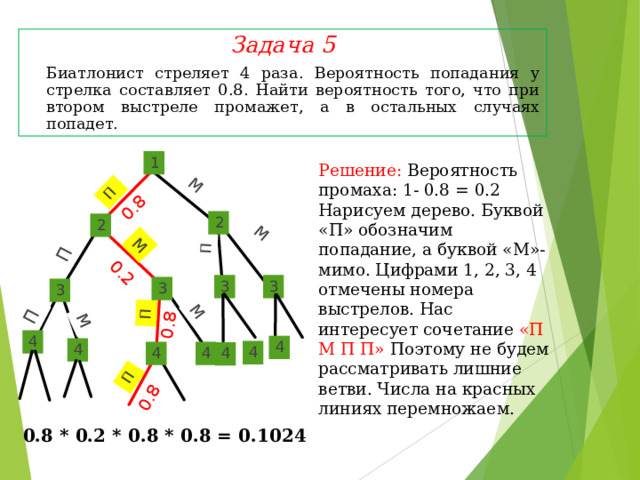
Задача 5

Биатлонист стреляет 4 раза. Вероятность попадания у стрелка составляет 0.8. Найти вероятность того, что при втором выстреле промажет, а в остальных случаях попадет.

1

Решение: Вероятность промаха: 1- 0.8 = 0.2 Нарисуем дерево. Буквой «П» обозначим попадание, а буквой «М»- мимо. Цифрами 1, 2, 3, 4 отмечены номера выстрелов. Нас интересует сочетание «П М П П» Поэтому не будем рассматривать лишние ветви. Числа на красных линиях перемножаем.

2

2

3

3

3

3

4

4

4

4

4

4

4

0.8 * 0.2 * 0.8 * 0.8 = 0.1024

Задачи на самостоятельную работу

• Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,32. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза
• Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,34. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Задачи на самостоятельную работу

• Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,9. Найдите вероятность того, что биатлонист первые 4 раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых
• Биатлонист 8 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,65. Найдите вероятность того, что биатлонист первые 4 раза попал в мишени, а последние четыре промахнулся. Результат округлите до сотых.
• Биатлонист 5 раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что биатлонист первые 4 раза попал в мишени, а последний раз промахнулся. Результат округлите до сотых

Задачи на самостоятельную работу

• Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 70% этих стекол, вторая — 30%. Первая фабрика выпускает 5% бракованных стекол, а вторая — 4%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным
• Две фабрики выпускают одинаковые стекла для автомобильных  фар. Первая фабрика выпускает 30% этих стекол, а вторая – 70%. Первая фабрика выпускает 4% бракованных  стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным

Спасибо за внимание