| Раздел долгосрочного плана: Раздел 5.3А: Текстовые задачи | Школа: КГУ ШГ № 6 | ||||
| Дата: | ФИО учителя: Новгородова И.Г. | ||||
| Класс: | Количество присутствующих: | отсутствующих: | |||
| Тема урока | Задачи на совместную работу. (5 часов, урок №3) | ||||
| Тип урока | Урок закрепления материала. | ||||
| Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу) | 5.5.2.3 решать текстовые задачи (например, задачи на совместную работу и т.д.) с помощью арифметических действий над обыкновенными дробями. | ||||
| Цели урока | Создают условия для актуализации знаний о производительности туда; составляют математические модели; решают задачи на совместную работу; записывают ответ. | ||||
| Критерии оценивания | Все учащиеся объясняют смысл выражений: «увеличить на столько»; «уменьшить в несколько раз»; решают простые задачи; записывают ответ. Большинство учащихся составляют план решения задачи; решают задачи с помощью арифметических действий над обыкновенными дробями; записывают ответ. Некоторые учащиеся решают задачи повышенной трудности, анализируют и составляют свои задачи; записывают ответ. | ||||
| Языковые цели | Предметная лексика и терминология: формула, скорость; расстояние; время, …; Серия полезных фраз для диалога: Чтобы найти расстояние, надо…. Чтобы определить скорость необходимо…. Для определения времени надо…. | ||||
| Привитие ценностей | Прививать патриотические чувства, используя семь незыблемых основ патриотического акта «Мәңгілік Ел». Развивать у учащихся коммуникативные компетенции (культуру общения и умение работать в группах). Ответственность за проведение взаимного оценивания, самооценивания. | ||||
| Межпредметные связи | История, экономика, физика, химия, окружающий мир | ||||
| Навыки использования ИКТ | Работа с интерактивной доской | ||||
| Предварительные знания | Арифметические действия и действия с обыкновенными дробями | ||||
| Ход урока | |||||
| Запланированные этапы урока | Запланированная деятельность на уроке | Ресурсы | |||
| Вызов 2 мин | Приветствие учащихся, формулировка темы урока, целей обучения, критериев оценивания | Презентация | |||
| Осмысление 7 мин 8 мин 15 мин 10 мин | 1) «Истина или Ложь» Учащиеся работают индивидуально. У каждого есть возможность выполнить самооценивание. Учащимся необходимо сделать вывод об истинности предложенных утверждений, используя карточки «Истина» или «Ложь». a) Если ширина b некоторого прямоугольника в5 раза больше длины aэтого же прямоугольника, тогда «Истина» b) Если скорость V1 легкового автомобиля на 20 км/ч больше скорости V2 грузового автомобиля, то
Ложь c) Если 2 кг яблок стоит aтг, то 3 кг яблок стоит 3a. «Ложь» d) Если площадь прямоугольника меньше площади S квадрата в 2 раза, то площадь прямоугольника равна «Истина» e) Если в настоящее время Сауле старше Ольги на 2 год, то через a лет она будет старше ее на Ложь 2) Работав группе Учащимся необходимо составить уравнения по условиям задач 24 т воды первый насос накачивает за 6 ч, а второй — за 3 часа. За сколько часов накачают 24 т воды два насоса, если будут работать вместе? 36 деталей первый рабочий изготавливает за 3 ч, а второй — за 6 ч. За сколько часов изготовят 36 деталей 2 рабочие, если будут работать вместе? Гончар может изготовить 12 кувшинов за 3 часа, а его ученик — за 6 часов. Сколько кувшинов могут изготовить мастер и ученик за 2 часа, работая вместе? Работу по ремонту кабинета школы выполняли две бригады. Первая бригада отремонтирует кабинет за 15 дней, а вместе со второй бригадой за 12 дней, за какое время с этой задачей справится вторая бригада?
3) Парная работа (оценивание учителем по следующим дескрипторам: - объяснять смысл выражений: «увеличить на столько»; «уменьшить в несколько раз» и т.п.; - составлять план решения задачи; - составлять математические модели; - решать задачи с помощью арифметических действий над обыкновенными дробями.) 1. Старинная задача из математической рукописи XVII века. «Два плотника рядились двор ставить. И говорит первый: - Только бы мне одному двор ставить, то я бы поставил за 3 года. А другой молвил: - Я бы поставил его в шесть лет. Оба решили сообща ставить двор. Сколько долго они ставили двор?» Ответ: Два плотника поставят двор, работая вместе за 2 года. 2. Лошадь съедает воз сена за месяц, коза за - два месяца, овца – за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена? Ответ:
4) Индивидуальная работа После составления уравнений учащиеся делятся условиями. Происходит процесс взаимооценивания. Составить условие задачи по заданному уравнению:
|
http://www.google.ru/url?sa=t&rct=j&q=&esrc=s&source=web&cd=5&ved=0ahUKEwjJ4pXuuL_TAhWDYJoKHYXjAfcQFgg6MAQ&url=http%3A%2F%2Fznanija.com%2Ftask%2F3947443&usg=AFQjCNF1m37aNAbDjeDsJiLyi0cGxo0Cng&cad=rjt
http://festival.1september.ru/articles/590890/
| |||
| Рефлексия 3 мин | В конце урока учащиеся проводят рефлексию: - что узнал, чему научился - что осталось непонятным - над чем необходимо работать Учащиеся оценивают свою работу по критериям: - объяснять смысл выражений: «увеличить на столько»; «уменьшить в несколько раз» и т.п.; - составлять план решения задачи; - составлять математические модели; - решать задачи с помощью арифметических действий над обыкновенными дробями. | Презентация | |||
| Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися? | Оценивание – как Вы планируете проверить уровень усвоения материала учащимися? | Здоровье и соблюдение техники безопасности | |||
| Дифференциация будет организована при индивидуальной работе и работе в парах. Учитель будет оказывать помощь сильным и слабым учащимся, а учащиеся среднего уровня будут продвигаться за счет взаимопомощи сильных учащихся. | Понимание теоретического материала через фронтальную беседу. Так же оценивание и взаимооценивание при индивидуальной работе и работе в парах | На начало урока учащиеся ознакомлены с правилами поведения в кабинете | |||
| Рефлексия по уроку Были ли цели урока/цели обучения реалистичными? Все ли учащиеся достигли ЦО? Если нет, то почему? Правильно ли проведена дифференциация на уроке? Выдержаны ли были временные этапы урока? Какие отступления были от плана урока и почему? | Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки. | ||||
|
| |||||
| Общая оценка
Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)? 1:
2: Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)? 1:
2: Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках? | |||||
Приложение 1 (раздаточный материал)
Парная работа
1. Старинная задача из математической рукописи XVII века.
«Два плотника рядились двор ставить. И говорит первый:
- Только бы мне одному двор ставить, то я бы поставил за 3 года.
А другой молвил:
- Я бы поставил его в шесть лет.
Оба решили сообща ставить двор. Сколько долго они ставили двор?»
2. Лошадь съедает воз сена за месяц, коза за - два месяца, овца – за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?
Индивидуальная работа
Составить условие задачи по заданному уравнению:
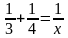
Парная работа
1. Старинная задача из математической рукописи XVII века.
«Два плотника рядились двор ставить. И говорит первый:
- Только бы мне одному двор ставить, то я бы поставил за 3 года.
А другой молвил:
- Я бы поставил его в шесть лет.
Оба решили сообща ставить двор. Сколько долго они ставили двор?»
2. Лошадь съедает воз сена за месяц, коза за - два месяца, овца – за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?
Индивидуальная работа
Составить условие задачи по заданному уравнению:
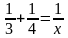
Парная работа
1. Старинная задача из математической рукописи XVII века.
«Два плотника рядились двор ставить. И говорит первый:
- Только бы мне одному двор ставить, то я бы поставил за 3 года.
А другой молвил:
- Я бы поставил его в шесть лет.
Оба решили сообща ставить двор. Сколько долго они ставили двор?»
2. Лошадь съедает воз сена за месяц, коза за - два месяца, овца – за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?
Индивидуальная работа
Составить условие задачи по заданному уравнению:
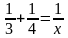

 Получите свидетельство
Получите свидетельство Вход
Вход


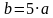 ;
;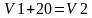 ;
;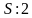 .
.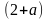 лет.
лет.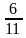 (месяца).
(месяца).








 Задачи на совместную работу (23.47 KB)
Задачи на совместную работу (23.47 KB)
 0
0 131
131 4
4 Нравится
0
Нравится
0









