Задачи на построение

Задачи на построение

1. Построение угла, равного данному.

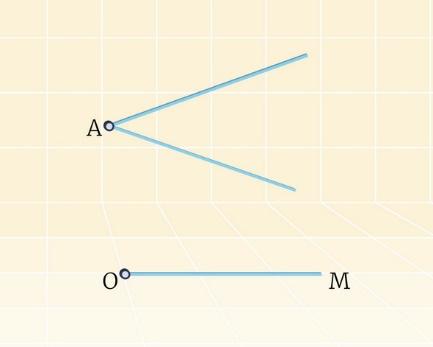
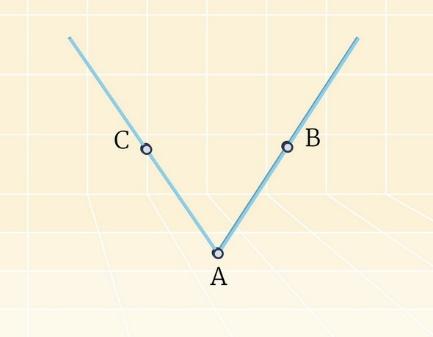
Дано: 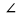 A, OM – луч.

Построить: ∠ EOМ = ∠ A.

Построение.

1. Окр. (A; r), r – произвольный радиус.

2. Окр. (A; r) ∩ AB = B.

3. Окр. (A; r) ∩ AС = С.

(АВ и АС стороны угла А)

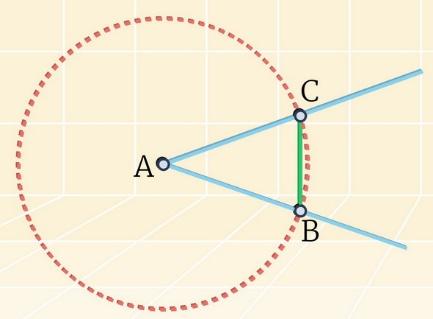
4. Окр. (O; r) ∩ OM = D.

5. Окр. (D; BС) ∩ Окр. (O; r) = E

6. OЕ, ∠ ЕОD = ∠BAC (из равенства ∆ОЕD и ∆ABC). ∠ EOM – искомый.

1. Построение биссектрисы угла

Дано: ∠ CAB.

Построить: AE – биссектриса ∠ CAB.

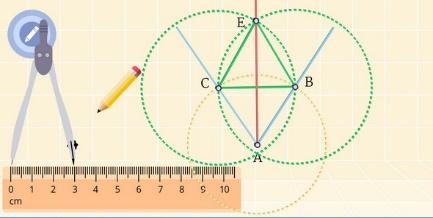Построение.

• Окр. (A; r), r – произвольный радиус.

• Окр. (A; r) ∩ AB = т.B.

• Окр. (A; r) ∩ AC =т. C.

• Окр. (C; CB) ∩ Окр. (B; CB) = т.E.

• AE – искомая биссектриса ∠BAC, т. к. ∠ABE =∠CBE (из равенства ∆ACE и ∆ABE).

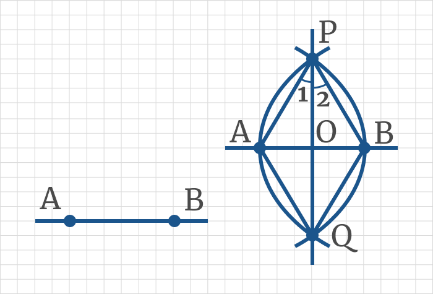3.Построение середины отрезка АВ.

Дано: отрезок АВ

Построить: т.О – середину отрезка АВ

Построение:

• Окр. (A; АВ), . окр. (В; АВ)

• Окр. (A; АВ) ∩ окр. (В; АВ) = т.Р.

• Окр. (A; АВ) ∩ окр. (В; АВ) = т. Q

• PQ ∩ AB = т.O – середина отрезка АВ

Доказательство. Для этого рассмотрим ∆APQ и ∆BPQ. Они равны по трём сторонам, следовательно, ∠1 = ∠2, поэтому РО– биссектриса равнобедренного ∆АВР, а соответственно РО ещё и медиана. Следовательно, точка О – середина отрезка АВ.

4.Построение треугольника по трем сторонам

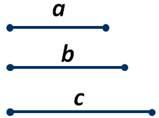Дано:

отрезки a, b, c.

Построить: ABC: AB = c , BC = a, AC = b

Построение:

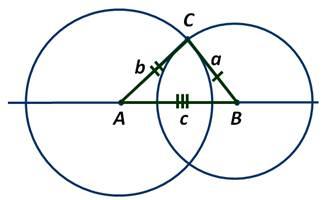• Отложим один из отрезков на произвольной прямой: AB = c

• Окр. (A; b), окр. (В; a)

• Окр. (A; b) ∩ окр. (В; a) = т.C

• отрезки АС и ВС.

• АВС искомый

Доказательство. Построение верно, так как у полученного треугольника АВС, АВ=c, АС=b, ВС=а.

Исследование. Задача имеет решение, если для данных отрезков выполняются неравенства:

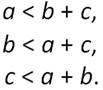
Если решение этой задачи существует, то оно является единственным, так как все построенные треугольники будут равны по трём сторонам, то есть по третьему признаку равенства треугольников.

5.Построение треугольника по двум сторонам и углу между ними.

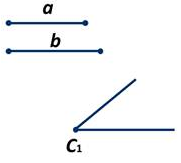Дано:

отрезки a, b, ∠С₁

Построить: ABC: BC = a, AC = b, ∠С = ∠С₁

Построение:.

• Проведём произвольную прямую и на ней отметим точку С.

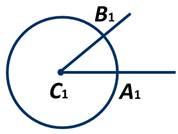• Построим ∠С=∠С₁

• Окр. (С₁; r), r - любой

• Окр. . (С₁; r) ∩ стороны ∠С₁ = т.А₁ и т. В₁

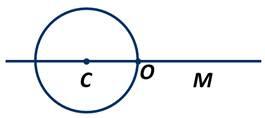
• Окр. (С; r)

• Окр. (С; r) ∩ луч СM = т. О.

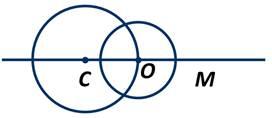• Окр.( О; А₁В₁)

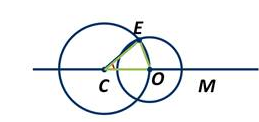• Окр. (С; r) ∩ Окр.( О; А₁В₁) = т.Е

• ∠МСЕ - искомый угол.

• отложить на одной стороне угла отрезок СА=b, а на другой - СВ=а.

• соединить точки А и В

• треугольник АВС - искомый.

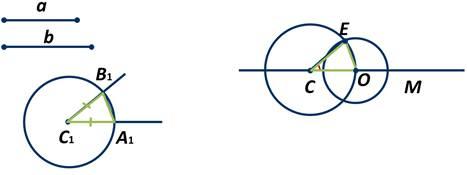Доказательство.

1.Докажем, что∠МСЕ - искомый угол.

Рассмотрим треугольники А₁В₁С₁ и ОСЕ: отрезки С₁А₁ и С₁В₁ равны как радиусы окружности с центром в точке С₁, а отрезки СО и СЕ - как радиусы окружности с центром в точке С. А так как по построению данные окружности имеют равные радиусы, то отрезки С₁А₁, С₁В₁, СО и СЕ равны между собой. А также у нас по построению В₁А₁=ОЕ.

Следовательно, треугольники А₁В₁С₁ и ОСЕ равны по третьему признаку равенства треугольников. Поэтому ∠А₁В₁С₁=∠ОСЕ. То есть построенный ∠МСЕ равен углу с вершиной в точке С₁.

Треугольник АВС является искомым.

Действительно верно, так как по построению сторона СВ=а, сторона СА=b, а ∠С=∠С₁.

Исследование. Задача имеет всегда единственное решение.

6.Построить треугольник по стороне и двум прилежащим к ней углам.

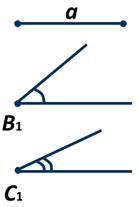Дано: отрезок а, ∠ В₁, ∠С₁

Построить:

АВС: ВС = а, ∠ В = ∠ В₁, ∠С = ∠С₁

Построение:

• Отложить на произвольной прямой отрезок ВС=а .

• Построить ∠ В = ∠ В₁, ∠С = ∠С_1.

• Точку пересечения лучей этих углов обозначить буквой А.

• АВС - искомый.

Доказательство:

Действительно верно, так как по построению сторона СВ=а, ∠ В = ∠ В₁, а ∠С=∠С₁.

Исследование:

Решение данной задачи существует только, если выполняется условие:

И если решение существует, то оно единственное, так как все построенные треугольники равны по второму признаку равенства треугольников.