Задачи на оптимизацию

Задачи на оптимальный выбор

«О собую важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека — как располагать своими средствами для достижения наибольшей выгоды»

Чебышев П.Л.

Для решения задач на оптимальный выбор наиболее часто используются:

1.М етод перебора вариантов 2.Метод логических рассуждений 3.Исследование функций элементарными методами 4.Исследование функций с помощью производной

1.Задача 16 ЕГЭ (Ценная бумага), метод перебора

Цена ценной бумаги на конец года вычисляется по формуле S   =  1,1 S 0  + 2000, где S 0   — цена ценной бумаги на начало года в рублях. Максим может приобрести ценную бумагу, а может положить деньги на банковский счёт, на котором сумма увеличивается за год на 12%. В начале любого года Максим может продать бумагу и положить все вырученные деньги на банковский счёт, а также снять деньги с банковского счёта и купить ценную бумагу. В начале 2021 года у Максима было 80 тысяч рублей, которые он может положит на банковский счёт или может приобрести на них ценную бумагу. Какая наибольшая сумма может быть у Максима через четыре года? Ответ дайте в рублях.

S , 1,12  1,1  + 2000, 100 000. 2) = 1,1∙ 80 000 + 2 000 = 90 000 руб. 3) = 1,1∙ 90 000 + 2 000 = 101 000 руб. 100 000 руб., положим деньги на счет. 4) = 1,12 ∙101 000 = 113 120 руб. 100 000 руб., положим деньги на счет. 5) = 1,12 ∙113 120 = 126 694,4 руб.- наибольшая сумма может быть у Максима через четыре года Ответ: 126 694,4 руб. " width="640"

1.Задача 16 ЕГЭ (Ценная бумага), продолжение

Решение:

• S   =  1,1 S 0  + 2000 – цена ценной бумаги, S 0 = 80 000 руб.

Через год цена ценной бумаги на счете в банке увеличивается в (100%+12%) : 100 = 1,12 раза.

Пусть руб.- сумма денег у Максима через n лет.

Узнаем когда надо положить деньги на счет

1,12 S , 1,12  1,1  + 2000, 100 000.

2) = 1,1∙ 80 000 + 2 000 = 90 000 руб.

3) = 1,1∙ 90 000 + 2 000 = 101 000 руб. 100 000 руб., положим деньги на счет.

4) = 1,12 ∙101 000 = 113 120 руб. 100 000 руб., положим деньги на счет.

5) = 1,12 ∙113 120 = 126 694,4 руб.- наибольшая сумма может быть у Максима через четыре года

Ответ: 126 694,4 руб.

2.Задание 16 ЕГЭ (2 поля) У фермера есть два поля, каждое площадью 10 га. На каждом поле можно выращивать картофель и свеклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле 400ц/га, а на втором - 300 ц/га. Урожайность свеклы на первом поле 300ц/га, а на втором - 400 ц/га. Фермер может продавать картофель по цене 10000 руб. за 1 ц, а свеклу - по цене 11000 руб. за 1 ц. Какой наибольший доход может получить фермер?

0,значит, у ( х ) возрастает на [0,10] ⇨наибольшее значение функция достигает при х = 10, у (10) = 700 000 ·10 33 000 000 = 40 000 000 руб. 3) 44 000 000 40 000 000 = 84 000 000 (руб.) - наибольший доход фермера. Ответ: 84 000 000 руб. " width="640"

2.Задание 16 ЕГЭ (2 поля) Метод логических рассуждений и монотонность линейной функции

Номер поля

Урожайность картофеля

1 поле, S=10 га

400 ц/га

Цена картофеля

2 поле, S=10 га

300 ц/га

Урожайность свеклы

10 000 руб. за 1 ц

300 ц/га

Цена свеклы

10 000 руб. за 1 ц

400 ц/га

11 000 руб. за 1 ц

11 000 руб. за 1 ц

Решение:

• На 2 поле выгоднее сажать свеклу, поэтому доход со второго поля составляет 400 · 11 000 · 10 44 000 000 (руб.).

2) Пусть на 1 поле под картофель заняли х га, х  [0,10] тогда под свеклу (10 х ) га. Доход с 1 поля равен х · 400 · 10 000 (10 х ) ·300 ·11 000 (руб.). Составим целевую функцию у у ( х ) и найдем ее наибольшее значение на [0,10].

у ( х ) х · 400 · 10 000 (10 х ) ·300 · 11 000,

у ( х ) 4 000 000 х 33 000 000 3 300 000 х ,

у ( х ) 700 000 х 33 000 000 - линейная функция, к = 700000 0,значит, у ( х ) возрастает на [0,10] ⇨наибольшее значение функция достигает при х = 10, у (10) = 700 000 ·10 33 000 000 = 40 000 000 руб.

3) 44 000 000 40 000 000 = 84 000 000 (руб.) - наибольший доход фермера.

Ответ: 84 000 000 руб.

3.Задача Дидоны (Монотонность квадратичной функции)   Среди прямоугольников с периметром Р найти прямоугольник с наибольшей площадью 

Легенда о Дидоне.

.. и женщина Дидона стала вождем надо всеми.

Она о своими спутниками вынуждена была бежать из родного города в Северную Африку, город Карфаген (Тунис).

Ей согласились уступить участок земли, но не больше чем объемлет воловья шкура

P = 2 x + 2 y , S = ху

3.Задача Дидоны (Монотонность квадратичной функции)

Решение:

Из формулы периметра прямоугольника P 2 x 2 y выразим у

у х, тогда S ху х ( х ). Составим целевую функцию S( х ) х ( х ), S( х ) х² х и найдем ее наибольшее значение на [0,Р].

S( х ) х² х − квадратичная функция , ее графиком является парабола,

а 1

х = длина прямоугольника, у ⇨ прямоугольник с наибольшей

площадью является квадратом со стороной

Ответ : квадрат со стороной

4 .ЕГЭ №16 Задача про 2 завода (производная)

Вадим является владельцем двух заводов в разных городах.

На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование.

В результате, если рабочие на одном из заводах трудятся суммарно t 2 часов в неделю, то за эту неделю они производят t единиц товара

За каждый час работы на 1 заводе Вадим платит рабочему 200 рублей, а на 2 заводе 300 рублей.

Вадим готов выделять 1 2 00 000 рублей в неделю на оплату труда рабочих.

Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Алгоритм решения задачи на оптимальный выбор

Шаг 1.   Выделить оптимизируемую величину y (величина, о наибольшем или наименьшем значении идет речь)

Шаг 2.   Определить независимую переменную х (одна из участвующих величин), определить ее реальные границы Шаг 3 .  Составить целевую функцию y = f(x) — это математическая модель задачи Шаг 4.   Исследовать полученную функцию и найти ее наименьшее или наибольшее значение

Шаг 5. Ответить на вопрос задачи

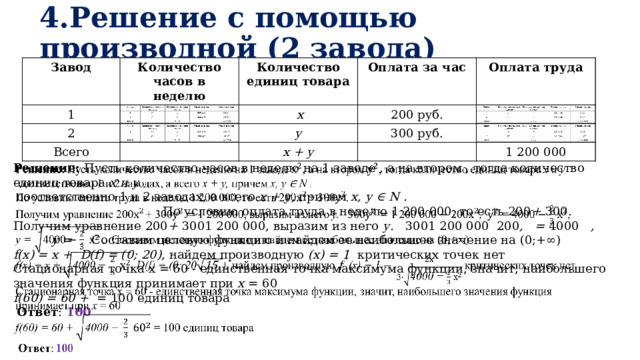
4.Решение с помощью производной (2 завода)

Завод

Завод

Количество часов в неделю

1

1

Количество часов в неделю

2

2

Количество единиц товара

Количество единиц товара

Всего

Всего

х

Оплата за час

Оплата за час

х

200 руб.

у

200 руб.

Оплата труда

Оплата труда

у

х + у

300 руб.

200

х + у

300 руб.

300

1 200 000

1 200 000

Решение: Пусть количество часов в неделю на 1 заводе , а на втором , тогда количество единиц товара х и у

соответственно 1 и 2 заводах, а всего х + у, причем х, у ∈ N . По условию оплата труда в неделю 1 200 000, то есть 200 + 300 .

Получим уравнение 200 + 3001 200 000, выразим из него у. 3001 200 000 200 , = 4000 , у = . Составим целевую функцию и найдем ее наибольшее значение на (0;+∞)

f(x) = х + D(f) = (0; 20), найдем производную (x) = 1 критических точек нет

Стационарная точка х = 60 - единственная точка максимума функции, значит, наибольшего значения функция принимает при х = 60

f(60) = 60 + = 100 единиц товара

Ответ : 100

Спасибо за внимание