МАОУ Одинцовский лицей №6 имени А.С. Пушкина
Презентация к уроку-семинару по учебному предмету «Информатика» в 11-ом классе на тему «Задачи оптимизации»
Автор: Шаталина Виктория Анатольевна
учитель информатики МАОУ Одинцовского лицея №6 имени А.С. Пушкина
г. Одинцово 2015
Семинар (лат seminarium - рассадник)
- вид практических занятий, который предусматривает самостоятельную проработку обучающимися отдельных тем и проблем в соответствии содержания учебной дисциплины и обсуждение результатов у этого изучения, представленных в виде тезисов, сообщений, докладов, рефератов и т.д.
Дидактические цели семинара
- развивать навыки умственной работы, творческого мышления, умения использовать теоретические знания для решения практических задач;
- формировать у обучающихся интерес к научно-исследовательской работе и привлечения к научным исследованиям, которые проводит кафедра информатики;
- обеспечивать системное повторение, углубление и закрепление знаний обучающихся по темам «Моделирование», «Компьютерные технологии», «Задачи оптимизации»
- показать связь математики и информатики с реальной действительностью; формировать умение наблюдать, обобщать, проводить рассуждения по аналогии; развивать мышление и речь учащихся
- формировать умение применять алгебраический и информационно-технологический аппарат и компьютерные технологии к изучению реальной действительности
Функции семинара
- - учебная (углубление, конкретизация, систематизация знаний, усвоенных во время теоритических уроков и в процессе самостоятельной подготовки к семинару);
- - развивающая (развитие логического мышления обучающихся, приобретение ими умений работать с различными компьютерными приложениями (ЭТ), формирование умений и навыков анализа данных, применяемых в задачах оптимизации);
- - воспитательная (воспитание ответственности, работоспособности, воспитание культуры общения и мышления, привитие интереса к изучению информатики, формирование потребности рационализации учебно-познавательной деятельности)
- - диагностически-коррекционная и контролирующая (контроль за качеством усвоения обучающихся учебного материала, выявление пробелов в его усвоении и их преодоления)
Ход ур о ка
- За неделю до проведения урока – семинара класс делится на 4 группы, каждая из которых получает индивидуальное задание.
- Все учащиеся группы решают 2 – 3 задачи, а один из них готовит сообщение или решение одной данной задачи для остальных учащихся класса.
Сообщение учащегося ( Исторический экскурс. Задача Дидоны )
Согласно легенде, вынужденная бежать из своего родного города, Дидона вместе со своими спутниками прибыла на северный берег Африки и хотела приобрести у местных жителей землю для нового поселения.
Ей согласились уступить участок земли, однако не больше, чем объемлет воловья шкура. Хитрая Дидона разрезала воловью шкуру на узкие ремешки, и разложив их, сумела ограничить гораздо большую площадь по сравнению с той, которую можно было покрыть одной шкурой.
Сообщение учителя
Представление решения задач по группам
Этапы решения задач оптимизации
- I этап. Постановка задачи
- Формализация задачи (Уточняющие вопросы)
- Формализация задачи (Уточняющие вопросы)
- II этап. Разработка модели Информационная модель (исходные, расчетные данные, результаты, Целевая Функция). Математическая модель (формулы). Компьютерная модель (в электронных таблицах).
- Информационная модель (исходные, расчетные данные, результаты, Целевая Функция).
- Математическая модель (формулы).
- Компьютерная модель (в электронных таблицах).
- III этап. Компьютерный эксперимент надстройка в ЭТ «Поиск решения» или «Решатель»: установка ЦФ, зависимой ячейки, ограничений.
- надстройка в ЭТ «Поиск решения» или «Решатель»: установка ЦФ, зависимой ячейки, ограничений.
- IV этап. Анализ результатов моделирования.
- Задача Дидоны очень сложная и относиться к специальному разделу высшей математики, так называемому вариационному исчислению. Ну, а мы с вами постараемся разобрать такие задачи, с которыми каждый из нас может встретиться.
I этап. Постановка задачи
Задача о наименьшем периметре
Формализация
Уточняющий вопрос
Ответ
Что моделируется?
Фигура, состоящая из двух объектов: ширины и длины.
Форма фигуры?
Прямоугольная.
Что известно о фигуре?
Размеры задаются длиной (а), шириной (b), площадью (S), периметром (Р).
В какой зависимости находятся объекты в фигуре?
Площадь равна произведению длины и ширины.
Что известно о площади?
Периметр – сумма длин всех сторон.
Площадь – величина постоянная, S=64см 2 .
Что известно о периметре?
Периметр должен быть наименьшим возможным.
Что надо определить?
Длины сторон прямоугольника при наименьшем периметре.
- Площадь прямоугольника 64 см 2 . Какую длину должны иметь его стороны, чтобы периметр был наименьшим?
- a – длина прямоугольника, b – ширина прямоугольника, S=64 см 2 - площадь прямоугольника, P – периметр прямоугольника.
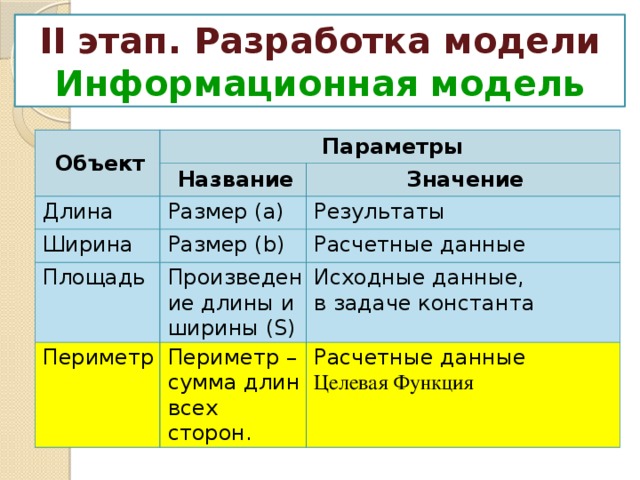
II этап. Разработка модели
Информационная модель
Объект
Параметры
Длина
Название
Размер (a)
Значение
Ширина
Результаты
Размер (b)
Площадь
Произведение длины и ширины (S)
Периметр
Расчетные данные
Исходные данные, в задаче константа
Периметр – сумма длин всех сторон.
Расчетные данные
Целевая Функция
II этап. Разработка модели
Математическая модель
S прям. =a*b - равно 64
Чтобы определить размер длины, нужно площадь прямоугольника разделить на размер ширины, т. е. b=S/a
P прям.= 2(a + b) – Целевая функция
II этап. Разработка модели
Компьютерная модель
Электронная таблица в режиме отображения формул
A
1
Площадь прямоугольника 64 см 2 . Какую длину должны иметь его стороны, чтобы периметр был наименьшим?
B
2
Длина =
C
3
Ширина =
4
5
Площадь =
результат
=B4/B2
Периметр =
расчет
64
дано
=2*B2+2*B3
ЦФ
=1, так как без него происходит ошибка деления на ноль. " width="640"
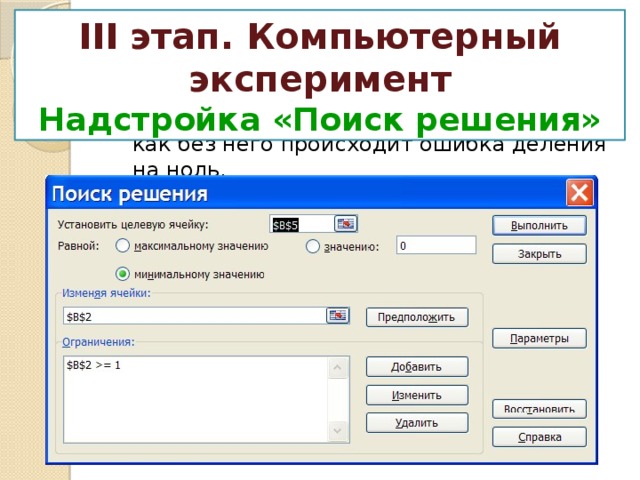
III этап. Компьютерный эксперимент
Надстройка «Поиск решения»
- Вводится ограничение: $B$2=1, так как без него происходит ошибка деления на ноль.
III этап. Компьютерный эксперимент
Надстройка «Поиск решения»
Изменим данные (пусть площадь будет равна 36 см 2 , 100 см 2 , 150 см 2 ) и проследим за пересчетом результатов.
A
1
2
B
Длина =
3
8
Ширина =
4
Площадь =
5
8
64
Периметр =
32
IV этап. IV этап. Анализ результатов моделирования
Наименьший периметр имеет геометрическая фигура квадрат
На основе полученных расчетов сделать вывод о длинах сторон для получения наименьшего периметра
Задачи других групп
- № 2 Задача о наибольшей площади
- № 3 Определение максимального объема коробки из квадратного листа
- № 4 Задача о кратчайшем пути
№ 2 Кусок проволоки длиной 48 м сгибают так, чтобы образовался прямоугольник. Какую длину должны иметь стороны прямоугольника, чтобы его площадь была наибольшей?
№ 3 Имеется квадратный лист картона со стороной а. Из листа делается коробка следующим образом: по углам листа вырезаются четыре квадрата, и коробка склеивается по швам. Какова должна быть сторона вырезаемого квадрата, чтобы коробка имела наибольшую вместимость?
№ 4 Буровая вышка расположена в поле в 9 км от ближайшей точки шоссе. С буровой надо направить курьера в населённый пункт, расположенный по шоссе в 15 км от упомянутой точки (считаем шоссе прямолинейным). Скорость курьера на велосипеде по полю 8 км/ч, а по шоссе 10 км/ч. К какой точке шоссе ему надо ехать, чтобы в кратчайшее время достичь населённого пункта?
Проверим задачу Дидоны
Среди замкнутых плоских кривых, имеющих заданную длину, найти кривую, охватывающая максимальную площадь. Как Дидона охватила шкурой большую территорию?
- Дидона изрезала шкуру быка на мелкие тесемки, связала их воедино и окружила большую территорию.
- Какую фигуру она использовала?
- Действительно ли многоугольник с большим количеством сторон при одинаковом периметре имеет большую площадь?
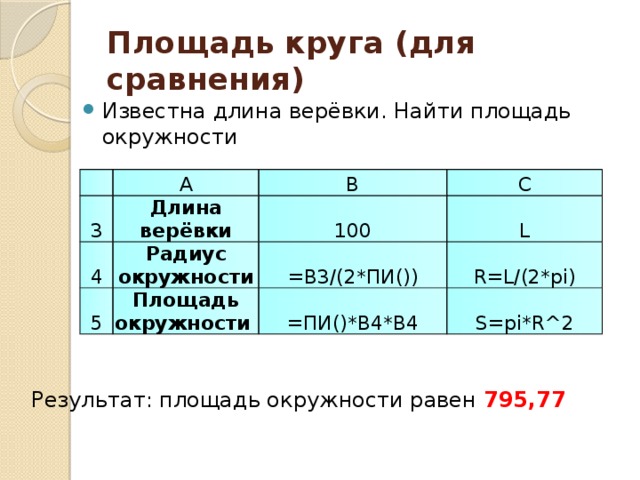
Площадь круга (для сравнения)
- Известна длина верёвки. Найти площадь окружности
А
3
Длина верёвки
В
4
5
С
100
Радиус окружности
Площадь окружности
L
=B3/(2*ПИ())
R=L/(2*pi)
=ПИ()*B4*B4
S=pi*R^2
Результат: площадь окружности равен 795,77
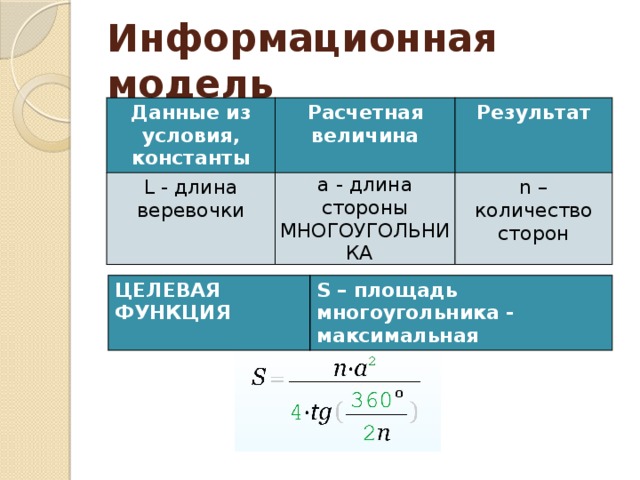
Информационная модель
Данные из условия, константы
Расчетная величина
L - длина веревочки
Результат
a - длина стороны МНОГОУГОЛЬНИКА
n – количество сторон
ЦЕЛЕВАЯ ФУНКЦИЯ
S – площадь многоугольника - максимальная
Математическая модель
- n — число сторон правильного многоугольника
- a — сторона правильного многоугольника
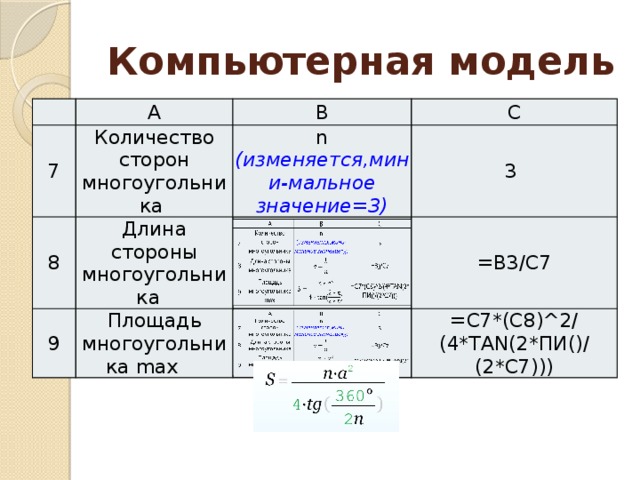
Компьютерная модель
А
7
А
7
B
8
8
Количество сторон многоугольника
B
Количество сторон многоугольника
9
Длина стороны многоугольника
n (изменяется,мини-мальное значение=3)
С
С
9
Длина стороны многоугольника
n (изменяется,мини-мальное значение=3)
Площадь многоугольника max
3
3
Площадь многоугольника max
=B3/C7
=B3/C7
=C7*(C8)^2/(4*TAN(2*ПИ()/(2*C7)))
=C7*(C8)^2/(4*TAN(2*ПИ()/(2*C7)))
Результаты
Вывод
- Гипотеза подтверждается.
- Действительно, многоугольник с большим количеством сторон имеет большую площадь
Количество сторон многоугольника
3
Площадь фигуры
481,125
5
688,191
500
795,764
800
795,770
Контрольное значение 795,77
Домашнее задание
№ 1 Старинная русская задача
- Пошла баба на базар, на людей посмотреть, да кое-что продать. Сколько надо взять бабе на базар для продажи живых гусей, уток и кур, чтобы выручить как можно больше денег, если она может взять товара не более P килограмм и известно, что:
Масса одной курицы - b1 кг, стоимость - c1 руб.;
Масса одной утки - b2 кг, стоимость - c2 руб.;
Масса одной гуся - b3 кг, стоимость - c3 руб.;
- Требуется определить, какое количество гусей, уток и кур (общей массой не более P кг) необходимо взять бабе на базар, чтобы выручка от продажи была максимальной.
Домашнее задание
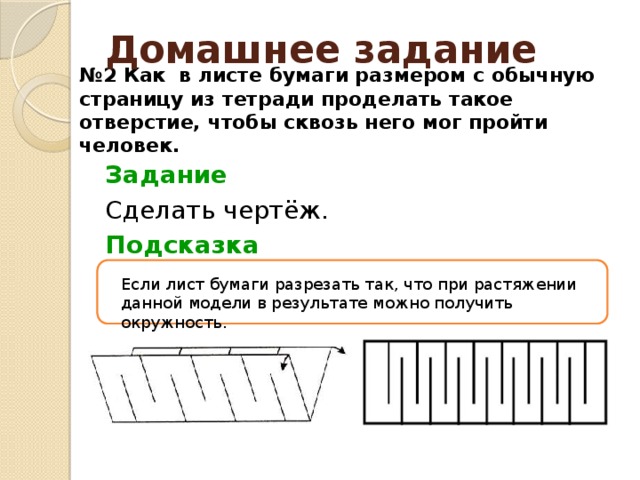
№ 2 Как в листе бумаги размером с обычную страницу из тетради проделать такое отверстие, чтобы сквозь него мог пройти человек.
Задание
Сделать чертёж.
Подсказка
Если лист бумаги разрезать так, что при растяжении данной модели в результате можно получить окружность.
Спасибо за внимание!
Автор презентации учитель информатики Шаталина В.А.
Получите свидетельство
Вход
Презентация к уроку-семинару по учебному предмету «Информатика» на тему «Задачи оптимизации» (0.62 MB)
0
588
22
Нравится
0
