С5 Финансовая математика Задачи на оптимальный выбор
Линейное нецелочисленное прогр-е
Фабрика, произв пищ полуфабр, вып блинчики с начинк ягодн и творож. В табл п себестоим и отпускная цена, а также производств возм фабрики по каждому виду продукта при полной загрузке всех мощн только данным видом продукта.
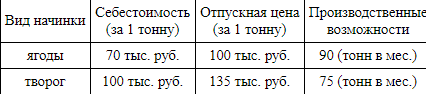
Для вып усл ассортимента, продукц каждого вида дб вы не менее 15 т. Предп, что вся продукия фабрики находит спрос (реализ без остатка), найди макс воз прибыль, кот м получ фабрика от произв блинчиков за 1 мес.
Реш Пусть x — доля мощн завода, занятых под произв блинч с ягодн начин, а y — доля мощн, занятых под произв блин с творо начинкой. Тогда x + y = 1, при этом блинч с ягод нач произ 90x т, а с твор начин— 75y т. Кр того, из усл ассортиментности следует, что ![]() откуда
откуда ![]() а
а ![]() откуда
откуда ![]() Прибыль завода с 1т продук с ягодной начин = 100−70 = 30 тыс.руб., прибыль с 1т продук с твор нач
Прибыль завода с 1т продук с ягодной начин = 100−70 = 30 тыс.руб., прибыль с 1т продук с твор нач
135 − 100 = 35 тыс. руб., общ прибыль с произвед за мес продукции ![]() Т t, н найти мах зн выр 75 · (36x + 35y) при вып усл:
Т t, н найти мах зн выр 75 · (36x + 35y) при вып усл:
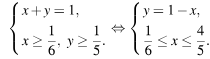 подст
подст ![]() получ
получ ![]() мах при
мах при ![]()
![]()
Максим прибыль ![]()
Линейное целочисленное прогр-е (есть геом интерпретация)
Зад17 № 508236В 1-е кл поступ 45 чел: 20 мальч и 25 дев. Их распре по двум кл: в одном д получ 22 чел, а в др ― 23. После распред посчитали процент девочек в каждом кл и получ числа сложили. Каким д б распределение по классам, чтобы получ сумма была наибольшей?
Реш 1. Вместо сумм % б считать сумм долю дев ― они отлич в 100 раз и достиг св макс одновр. Каждая дев в кл из 22 чел сост 1/22 от общего числа уч в этом кл, а в кл из 23 чел 1/23 от об числа учащ Зн, если поменять местами дев из большего кл и мальч из меньше, сумм % дев вырастет. Таким обр, макс достиг, когда все подоб перестан сделаны, т е, когда меньш класс полн сост из девочек, а в большем кл ― 3 девочки и 20 мальчиков.
Реш2. Пусть в меньш класс распр х дев (где 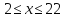 ), тогда в больший кл попало дев 25-x. Зн, сумм доля дев в двух кл=
), тогда в больший кл попало дев 25-x. Зн, сумм доля дев в двух кл= ![]() и предст лин функ с положит угл коэфф. Зн, эта функ достигает св наиб знач на правом конце промеж [2; 22], т е при x=22
и предст лин функ с положит угл коэфф. Зн, эта функ достигает св наиб знач на правом конце промеж [2; 22], т е при x=22
Таким обр меньш класс полн д сост из девочек, а в большем кл д б 3 дев и 20 мальчиков.
512995 Предпр купил здание и собир открыть в нём отель. В отеле м б станд номера п 27 кв м и «люкс» пл 45 кв м. Общая пл, кот м отвести под номера, сост 981 кв м. Предпр м поделить эту пл меж ном разл типов, как хочет. Обычн номер б приносит отелю 2000 руб в сут, а люкс — 4000 руб в сут. Какую наиб сумму денег см заработать в сутки на своём отеле предприниматель?
Реш. Пусть в отеле х ном пл 27 кв. м и у ном пл 45 кв. м. Тогда ![]() или
или ![]()
Прибыль, кот принос эти номера, ![]() или
или ![]() Прибыль б наиб при наиб зн суммы
Прибыль б наиб при наиб зн суммы ![]() Пусть
Пусть ![]() тогда
тогда ![]() откуда, подст в после нер-во, получаем:
откуда, подст в после нер-во, получаем:
![]() В сл рав наиб зн суммы s соотв бы наиб зн вел у. В сл нер-ва н найти наиб возм зн y и пров меньшие зн, уменьш кол пустого пр=ва.
В сл рав наиб зн суммы s соотв бы наиб зн вел у. В сл нер-ва н найти наиб возм зн y и пров меньшие зн, уменьш кол пустого пр=ва.
Наиб возм зн у = 21. Т к ![]() для получ наиб прибыли н откр 21 н люкс и 1 станд номер, кот б приносить п доход
для получ наиб прибыли н откр 21 н люкс и 1 станд номер, кот б приносить п доход ![]() руб. в сут. При этом ост 9 кв.м. незанят пр=ва. Умень на 1 кол люксов. Если в гостин 20 люкс и 3 станд номера, незанят пр-ва не ост:
руб. в сут. При этом ост 9 кв.м. незанят пр=ва. Умень на 1 кол люксов. Если в гостин 20 люкс и 3 станд номера, незанят пр-ва не ост: ![]() В этом сл доход тот же руб. дальн уменьш кол люксов в пользу станд ном привед к уменьшению прибыли. Те, в отеле д б как м больше ном пл 45 кв. м.
В этом сл доход тот же руб. дальн уменьш кол люксов в пользу станд ном привед к уменьшению прибыли. Те, в отеле д б как м больше ном пл 45 кв. м.
513295 Предпр купил здание и хочет отк в нем отель. В отеле м б станд номера пл 30 кв ме и люкс» пл 40 кв м. Общая пл, кот м отвести под номера, сост 940 кв м. Предпр м опр эту пл между номе разли типов, к. Обычный номер б принос отелю 4000 руб в сут, а люкс — 5000 руб в сутки. Какую наиб сумму денег см зараб в сутки на св отеле предпр? Отв: 125 000 руб.
Т1)У фермера 2 поля, каждое пл 10 га. На каждом м выращ кар и свёклу, поля м делить меж ними в любой пропор. Урож карто на 1 поле 300 ц/га, а на 2м – 200 ц/га. Урожайн свёклы на 1 поле 200 ц/га, а на 2м – 300 ц/га.м продав картоф по цене 10 000 р/ц, а свёклу – по цене 13 000 р/ц. Какой наиб доход м получить фермер?
| 1 поле | S | Урожай | Выручка |
| картофель | х га | 300 х ц | 10 000 |
| свёкла | 10 – х га | 200(10 – х) ц | 13 000 |
| Всего |
|
| 26 |
| 2 поле | S | Урожай | Выручка |
| картофель | у га | 200 у ц | 10 000 |
| свёкла | 10 – у га | 300(10 – у) ц | 13 000 |
| Всего |
|
| 39 |
Общий доход:
26 + 39
= р
4х – 19у + 650 = с у = где х
найдём с при кот у=мах: Ц ф – мн-во прямых, паралл прямой у =
Рассм 2 угл крайн т(0;10) и (10;0), подст их к-ты найдём наиб зн с = 690 умн на 10000 отв
Квадратичное программирование
№ 511227 В распоряж нач имеется бригада раб в сост 24 чел. Их н распред на день на 2 объекта. Если на 1м объекте раб t чел, то их суточ зарпл сост 4t2 у. е. Если на 2м объекте раб t чел, то их сут зарп сост t2 у. е. Как н распред на эти объекты бригаду рабоч, чтобы выплаты на их суточ зарпл оказ наименьшими? Ск у. е. в этом сл придется заплатить рабочим?
Реш Пусть на 1й об б напр х раб, сут зарпл кот сост Тогда на 2й об б направ раб
— сут зарпл сост В день начальн д платить рабочим
Рассм ф f(x) при Это квадр ф старший коэфф положит, след она имеет наим зн при x0 = 4,8. т мин не явл нат числом, поэтому иссл ф достиг наим з в т 4 или в т 5. Найдем и сравним эти значения:
на мн-ве нат зн арг наим зн функ в т 5. Поэтому н направ 5 раб на 1 объект, 19 раб — на2 объект. Зарпл раб сост 461 у. е.
Подобная https://easy-physic.ru/4-sposoba-resheniya-odnoj-zadachi-na-optimalnyj-vybor/
Г влад 2 завод в разн городах. произв одинак товары, если раб на заводе1, трудя сумм часов в нед, то за эту нед они произв 3t ед товара; если раб на заводе 2 , трудят сумм
час в нед, то за эту нед они произв 4t ед тов. За кажд час раб (на каждом из зав Г платит раб 500 руб. Г готов выдел 5 млн руб в нед на опл труда раб,. Какое наиб кол ед товара м произв за неделю на этих 2 заводах?
на 1 зав раб часов, а на 2м –
час. Тогда на 1 зав они произв 3x продукц, а на 2м –4y
Если Г платит 5 млн в нед, и в то же вр 500 руб/час, то итак зад сведась к
при
1 способ через производную
2 способ геом -окружность н отыск касат к окружн
Изв, чтобы прямые и перпенд, д вып
. Поэтому, если у нашей прямой коэф при y =3/4 , то у касат он д б =-4/3 т е
3 способ аналит геом прямая причем С и есть реш. Найдем расст от этой прямой до т с коорд
4 способ тригон Переходим в полярные к-ты: тогда
максим зн при и равно 500
№509184 Первичн информ разд по серверам 1 и 2 и обраб на них. С сервера1 при объёме Гб вх в него инф выходит 20t Гб, а с сервера №2 при объёме
Гб вх в него инф вых 21t Гб обраб инф, 25 t tм объёме вх информ в 3364 Гб?
Реш Пусть на серв 1 обраб а на серв 2 Гбайт из всей первичн инф. Тогда
а обраб будет Гб Н. найти мах при усл
(1) т к то
где
Мах зн суммы достиг при
т е для зн, удовл усл (1)
2 сп. н найти мах
X=40— т макс функ, при этом Усл выполн
3 сп геом. Уравн зад окружн рад 58 с центром в нач коорд задает семейство паралл прямых мах С при касании Проведем из нач коорд в 1 квадрант вектор перпенд прямым Луч, коллин пересечёт окружн в т Это и б т касания в кот достиг мах С Усл для точки вып
511234 Два велосипед равном движутся по вз перпенд дорогам по напр к перекр этих дорог. 1q движется со скор 40 км/ч и нах на расст 5 км от перекр, 2й движ со скор 30 км/ч и нах на расст 3 км от перекр. через ск мин расст меж велосипед станет наим? Каково б это наим расстояние.
расст между ними м б выч по т Пифагора. Расс тf (t) — квадрат длины в каждый мом времени,
Итак, У данной квадр функ есть наим зн, кот достиг при мин.
Таким обр мин расст меж велосип км, и б достигн через .
511919Ал вышел из дома на прогулку со скор v км/ч. После того, как он прошел 6 км, из дома следом за ним выбежал собака Ж, скорость кот б на 9 км/ч больше скорости Ал. Когда Ж догнала хозяина, они поверн назад и вместе возвр домой со скоростью 4 км/ч. Найдите зн v, при кот время прогулки Ал окаж наим. Ск при этом составит время его прогулки?
Реш Скорость сближ Ал и Ж (разн скор) Δv = 9 км/ч. Первонач разность расст меж Ал и Ж ΔS = 6 км. Найдем разност отн часа. Это и есть время, кот потреб Ж, чтобы догнать Ал.С того времени, как Ж бежала за Ал, Ал прошел расст, 2/3 км. по с усл Ал прошел еще 6 км пока Ж была дома. Зн, в напр от дома Ал,, прошел 6+2/3км. Такой же путь Ал прошел после того, как Ж догнала его, но в обр напр. На преодол этого пути (со скор 4 км/ч) надо
час. вся прогул Ал продлил Эта сумма =мин при это при
=1 v = 6 км/ч. Время всей прогулки Ал час.
512339 Произв x тыс. е продукц об в q = 0,5x2 + x + 7 млн ру в год. При цене тыс. руб за ед год прибыль от продажи этой продук (в млн руб) сост px − q. При каком наим зн p через 3 года сумма прибыль сост не менее 75 млн рубл?
Реш рибыль (в млн руб) за 1год
Прибыль составит не менее 75 млн руб, если т е
При наим цена 9 тыс. руб
№ 512381 Произв x тыс. е продукц обх в q = 0,5x2 + 2x + 5 млн руб в год. При цене p тыс. руб за ед годо прибыль от продажи этой продукц (в млн руб) сост px − q. При каком наим зн p через 4 года сумм прибыль сос не менее 52 млн руб?
Реше Прибыль (в млн руб) за 1 год наиб зн при x = p – 2 и сост Через 4 года прибыль сост не менее 52 млн руб
т е при
ПРОЧИЕ
№ 511919 Садовод привез на рынок 91 кг ябл, кот после перевозки разд на 3 сорта. Ябл 1 сорта он продав по 40 руб., 2 сорта – по 30 руб., 3 сорта – по 20 руб. за кг. Выручка от продажи всех яб сост 2170 руб. Изв, что масса ябл 2-го сорта
Пусть x кг — масса ябл 1-го сорта, y кг — масса ябл 2-го сорта, ост 91 − (x + у) кг —масса ябл 3-го сорта. Для вел выручки имеем: откуда y=35-2x т к масса ябл 1-го сорта
садовод продал 7 кг яблок 1 сорта и, следоват 35 − 14 = 21 кг яблок 2 сорта.
2 способ. Пусть x кг — масса ябл 1 сорта, прод садоводом, а масса ябл 2 сорта tx кг. Тогда масса проданных яблок 3сорта с tx · t = t2x кг. По усл задачи
: делим (2) на (1)
2 корень не подх
x найдем из уравн
Квадратичное программирование
1)В коллективе зарплата плата каждого рабочего Q руб. Число занятых на производстве мест – х. Зар плата и число раб мест связаны соотн
Согласно «золотому п-лу роста» найти х так, чтоб Q принимало наибольшее возможное зна-чение. При L 1500, a 16 000 найти по этому правилу число раб мест, если дополнительно известно, что трудовой коллектив располагает рабочими местами.
при
на отр1; 25 производная Qх ,прох через единств стац т x 20, меняет з с + на -, то функция в этой т достигает наиб значения Таким обр, зар плата рабоч б достигать наиб разм, если работодат организ на участках 15, 18 и 20 раб мест
2)Завод изготавл и продает полупровод приборы. Удельные расходы (в расчете на 1 прибор) зависят от объема производства и включают в себя постоянную часть в размере 1000 (руб/прибор) и переменную часть 2n (руб/прибор), где n − число приборов, изготовленных за месяц. Цена прибора, в свою очередь, зависит от объема производства по закону p(n)=10000−n (руб/прибор). Определить, при каком объеме производства прибыль будет максимальной?
Решение. Доход от продажи приборов, изготовленных в течение месяца,
.
Месячные расходы при этом Тогда прибыль
Исследуем функцию прибыли на экстремум. будем считать, что n действительное число. Дифференцируя по n, получаем:
2 производная всюду
3)На изготовление x единиц товара фирма затрачивает C(x)=ax2+bx руб,где a и b − действительные числа. Товар продается по цене p руб за штуку. Определить объем продаж, при котором прибыль наибольшая
Решение. При продаже x ед товара фирма получает доход , прибыль фирмы
Найдем производную функции P(x)
Рассмотрим 2ю производную: Т к она -точка максимума, т.е. при данном объеме продаж прибыль фирмы будет наибольшей.
4) Зависимость объема производства Q от количества работников L описывается функцией Q(L) (рис).
Показать, что если производные удовлетворяют условиям то
существует оптимальное число работников L∗, при котором прибыль будет наибольшей.
Решение. Условия Q′(L)0,Q′′(L)
где p − цена продажи ед продукции, Q(L) − объем производства, qL − часть расходов, связанная с работниками, C − постоянная часть расходов, не зависящая от числа работников
Исследуем возможный экстремум этой функции. 1я производная имеет вид:
Функция прибыли P(L) имеет критическую точку L∗ при условии
Так как 2я производная L, то критическая точка является точкой максимума. в заданной системе всегда существует оптимальное количество работников L∗, при котором прибыль предприятия максимальна
3). Расстояние между 2 фермами А и В п дороге 60 км. На ферме А надаивают 200 т молока в сутки, на ферме В – 100 т в сутки. Где построить завод по переработке молока, чтобы для его перевозки количество тонно-километров было наименьшим?
Решение АС =х, ВС =60 – х. Количество т-км, пройденных транспортом от А до С за каждый
день, 200 х т/км, а от В до С – 100 (60 – х) т/км. Суммарное количество т-км выразится
функцией у = 200х + 100 (60 – х) = 100х + 6000, которая определена на отрезке [0; 60].
Исследуя функцию у = 100х + 6000 на отрезке [0; 60],
получим : = 6000. Вывод: Завод надо строить возле фермы А.
Вывод2: если на ферме А добывается молока больше, чем на ферме В, то завод надо строить
возле фермы А; если же количество молока на этих фермах одинаковое, то завод можно
строить в любом месте вблизи шоссейной дороги между фермами А и В.
Нелинейная оптимизация
Города A и B на расстоянии a км и соединены прямой жел дорогой. Для перевозки грузов из A в C, отстоящий от жел дороги на b км, надо построить авто дорогу, примыкающую к железной дороге (рис). К какой точке S следует провести шоссе, чтобы транспортировка грузов была наиб экономичной? Стоимость перевозки 1 т груза на 1 км p руб. по жел дороге и q руб. по авто дороге.
Реш пусть x расстояние от города A до автом съезда S. Тогда стоимость перевозки 1 т груза по железнодор участку AS
Длина автомоб участка пути SC определяется по теореме Пифагора
Обозначим cтоимость перевозки 1т по автодороге,
полную стоимость.
Для исследования экстремальных значений функции Q(x) найдем ee производную:
Приравнивая производную нулю, вычисляем критическое значение x
Как изменяется знак производной при переходе через найденное критическое значение?. В выражении для производной П в левой окрестности критической точки производная будет 0. Таким образом, данная точка соответствует минимуму функции Q(x) решение действительно лишь при условии qp, т.е. удельные расходы по перевозке грузов по авто дороге должны превышать расходы при транспортировке по жел дороге. Это условие,, не является единственным ограничением на возможные значения p и q. Исследуя диапазон значений, в котором может изменяться отношение q/p рассмотрим 2 предельных случая:
Если x=0, то получаем следующее решение:
Это отношение удельных расходов q/p является минимально возможным. При этом значении q/p надо строить авто дорогу сразу вдоль диагонали AC.
Другой предельный случай соответствует решению x=a
Здесь отношение
Ясно, что на практике это отношение конечно, т.е. оптимальная точка ответвления всегда будет находиться в промежутке 0≤x
513717 В мечт о собств квартире, кот стоит 2 млн руб. В м купить ее в кредит, при этом банк готов выдать эту сумму сразу, а погаш кредит В придет 20 лет равн ежемес платеж, при этом ему придется выпл сумму, на 260% превыш исх. Вместо этого, В м какое-то время снимать кварт (стоим аренды – 14 тыс. руб. в мес), откл каждый мес на покупку кв сумму, кот ост от его возм платежа банку (по 1й сх) после уплаты аренд платы за съемн кварт. За ск меся в этом сл Ва см накопить на кварт, если считать, что стоимость ее не изменится?
Реш. Пусть Вкупил квартиру в кредит. Тогда он допогасить кредит за 20 лет, т е за 240 одинак ежемес платежей. Сумма, кот он д выпла банку, по усл на 260% превыш исх 2 млн. руб., т е,= 2000 · 3, 6 = 7200 тыс. руб. Раздеэту сумму на 240, получаем ежемес платеж, 30 тыс. руб.Далее, если вместо этого В снимал квартиру, то после оплаты аренды у него б ост ежемес16 тыс. руб. Поск 2000 : 16 = 125 мес т е за 10 лет и 5 мес.
Примеры задач целочисленной оптимизации
4). На участке нужно провести водопровод длиной 167 м. есть трубы длиной 5 м и 7 м. Сколько брать тех и других труб, чтобы сделать наименьшее количество соединений (трубы не резать)?
Реш:, количество 7м труб обозн х, а 5–м – у. Тогда 7х – длина 7-м труб, 5у – длина 5-м труб.
получаем неопределенное уравнение: 7х + 5у = 167 которое нужно решить в целых числах.
Выразив, например, у через х, получим:
Т к х, у Є Z, то методом перебора легко найти пары значений х и у, которые удовлетворяют уравнению 7х + 5у = 167. Если то х не является целым числом.
Если 2х – 2 =0, то х = 1, у =32. Если 2х – 2 =10, то х =6, у = 25.
Если 2х – 2 =20, то х = 11, у = 18. Если 2х – 2 =30, то х = 16, у = 11.
Если 2х – 2 =40, то х = 21, у = 4. Если 2х – 2 =50, то х = 26 и 7 ∙26 = 182 167.
получили пары решений: (1; 32), (6; 25), (11; 18), (16; 11), (21; 4).Из этих решений наиболее выгодное последнее, т.е. х = 21, у = 4.
Вывод: Надо взять 21 трубу длиной по 7 м и 4 трубы длиной по 5 м.
5 )Известно, что 1кг апельсинов содержит 150мг витамина С, а 1кг яблок -
75 мг витамина «С». Сколько апельсинов и сколько яблок следует включить в дневной рацион, чтобы при ми затратах в нем оказалось 75 мг витамина «С», не менее 0,25кг апельсинов и не менее 0,25кг яблок, если 1кг апельсинов стоит 60р., а 1кг яблок– 40р.?
Ограничения имеют вид: х ≥ 0,25; у ≥ 0,25; 150х + 75у = 75.
Целевая функция: F (х, у) = 60х + 40у.
Надо найти такие х и у, при которых целевая функция принимает минимальное значение. Построим область допустимых решений задачи:
Пусть 60х + 40у = 0; отсюда у = -6/4х
Построим график функции у = -6/4х и выполним параллельный перенос его вдоль оси ОУ вверх, т.е. это равносильно увеличению значений выражения 60х + 40у. Чтобы целевая функция принимала минимум, ее график должен пересечь отрезок М1М2 в точке М2. Она является точкой пересечения прямых у = 0,25 и у = -2х +1.
Отсюда, у = 0,25, х = 0,375. Далее находим: F (х, у) = 60∙0,375 + 40∙0, 25 = 16,25р.
Итог: Чтобы дневной рацион содержал 75мг витамина С и чтобы затраты при этом были миним, человеку необходимо ежедневно съедать 0,375кг апельсинов и 0,25кг яблок.
Максимум дискретной посл-ти
1) Пф владеет цен бумаг, кот стоят тыс. руб в конце года В конце любого года пф продать ценные бум и полож деньги на счёт в банке, при этом в конце каждого след года сумма на счёте б увел в 1+r раз. Пф хочет продать цен бумаги в конце такого года, чтоб в конце 25 г сумма на его счёте б наиб. Расчёты показали, что для этого бумаги н продав строго в конце 21 г. При каких положит зн r это возм?
Реш если пф продаст ценные бумаги в конце кода k, то в конце 25 г на его счёте будет ты сруб ошибка решать - это необх но не достаточное усл

 Получите свидетельство
Получите свидетельство Вход
Вход











 Задачи на кредиты С17 (588.92 KB)
Задачи на кредиты С17 (588.92 KB)
 0
0 317
317 15
15 Нравится
0
Нравится
0






