Задача по математике №17 егэ

Задачи экономического содержания в ЕГЭ № 17

Автор : Прудников Андрей

Викторович,

учитель математики

Карачев

2019

Актуальность:  

В вариантах ЕГЭ-2015 по математике появилась новая задача №19 – задача с экономическим содержанием. Позднее – задача №17.

Эта специфическая задача оказалась сюрпризом не только для школьников, но даже для учителей. С чего начать решение? Где взять формулы? На что вообще похожа эта задача и почему в вариантах ЕГЭ она расположена между сложными 16 и 18?

Самое необходимое для решения задачи 17

• 1) 1% - это 0,01
• 2) Основные соотношения и выражениями, встречающиеся при решении задач на проценты:
• Число a составляет p% от числа в :
• a = 0,01bp
• Число а увеличили на p%:
• a·(1+0,01p)
• Число а увеличили сначала на p%, а потом еще на q%:
• a·(1+0,01p)·(1+0,01q)
• Число а уменьшили на p%:
• a·(1 - 0,01p)

• Задачи, связанные с изменением величины
• Пусть S o – первоначальная величина, S – новая величина.
• Повышение на a% n раз на a%
• S= S o ·(1+0,01a) S= S o ·(1+0,01a) n
• Понижение на a% n раз на a%
• S= S o ·(1-0,01a) S= S o ·(1-0,01a) n

Тематика задач

• Задачи на кредиты с равными платежами
• Задачи на кредиты с дифференцированными платежами
• Задачи на вклады и инвестиции
• Задачи на наибольшее и наименьшее значение, решаемые при помощи производной

Задачи на погашение кредита равными платежами. Общая формула.

• Для подсчета величины в скобках иногда применяется формула суммы n членов геометрической прогрессии.
• Здесь b1 =1, q = p.
•   Напомним формулу для суммы n членов геометрической прогрессии:

В нашем случае, размер долга через n лет

Пример 1.

• В июле планируется взять кредит на сумму 8052000 рублей. Условия его возврата таковы: - каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить некоторую часть долга Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами (то есть за 4 года)?

Решение:

• Пусть S (рублей) - нужно платить ежегодно.
• 1 год:
• В январе сумма долга составит 8052000*1,2 = 9662400.
• После 1 платежа сумма долга станет равна 9662400 - S .
• 2 год:
• В январе сумма долга составит (9662400 - S)*1,2.
• После 2 платежа сумма долга станет равна (9662400 - S)*1,2 - S.
• 3 год:
• В январе сумма долга составит ((9662400 - S)*1,2 - S)*1,2.
• После выплаты сумма долга станет равна ((9662400 - S)*1,2 - S)*1,2 - S.
• 4 год:
• В январе сумма долга составит (((9662400 - S)*1,2 - S)*1,2 - S)*1,2.
• После 4 платежа сумма долга станет равна (((9662400 - S)*1,2 - S)*1,2 - S)*1,2 - S.
• Так как кредит был погашен 4 равными платежами, то после 4 платежа долга не осталось, т.е.
• (((9662400 - S)*1,2 - S)*1,2 - S)*1,2 - S = 0.

• Решим это уравнение и найдем S.
• ((9662400*1,2-1,2S - S)*1,2 - S)*1,2 - S = 0,
• (9662400*1,2 2  - 2,64S-S)*1,2 - S = 0,
• 9662400*1,2 3  - 4,368S - S = 0,
• 5,368S = 9662400*1,2 3 ,
• S = 3 110 400.

Пример №2

• В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы: - каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; - с февраля по июнь каждого года необходимо выплатить часть долга, равную 2,16 млн рублей. Сколько млн. рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами (то есть за 3 года)?

Решение:

• Пусть в банке было взято X млн. руб.
• 1 год:
• В январе сумма долга будет составлять 1,2 X.
• После 1 платежа сумма долга составит: 1,2 X - 2,16.
• 2 год:
• В январе сумма долга будет составлять 1,2⋅(1,2X−2,16)=1,22⋅X−2,592.1,2⋅(1,2X−2,16)=1,22⋅X−2,592.
• После 2 платежа сумма долга составит: 1,22⋅X−1,2⋅2,16−2,16=1,22⋅X−4,7521,22⋅X−1,2⋅2,16−2,16=1,22⋅X−4,752.
• 3 год:
• В январе сумма долга будет составлять 1,2⋅(1,22⋅X−4,752)=1,23⋅X−5,70241,2⋅(1,22⋅X−4,752)=1,23⋅X−5,7024.
• После 3 платежа сумма долга составит: 1,23⋅X−5,7024−2,16=1,23⋅X−7,86241,23⋅X−5,7024−2,16=1,23⋅X−7,8624.
• Так как кредит был погашен 3 равными платежами, то после 3 платежа долга не останется, т.е. станет равным 0.

• 1,23⋅X−7,8624=0
• 1,23⋅X=7,8624
• X=4,55
• То есть в банке было взято 4,55 млн. руб.

Ответ: 4,55

Кредиты с дифференцированными платежами

• Пример №1

Предприятие взяло в банке кредит на 5 лет. Условия погашения кредита следующие: по истечении каждого года заемщик погашает банку начисленные проценты за год и 1/5 часть основной суммы. Какой процент годовых установлен банком по этому кредиту, если общая сумма выплат предприятия банку на 24% превышает размер исходного кредита?

№

№

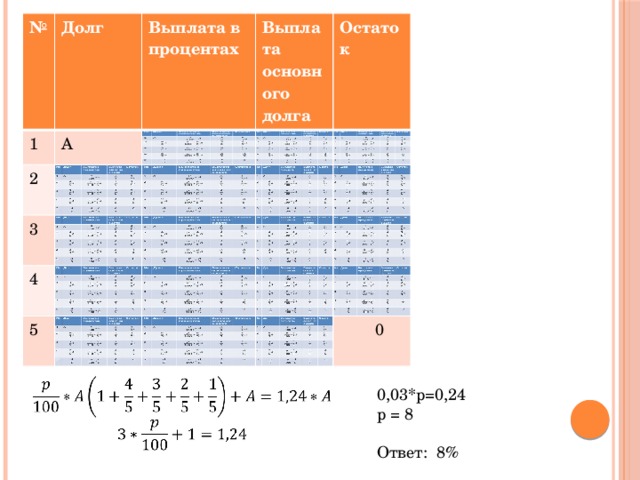
Долг

1

1

Долг

А

А

Выплата в

Выплата в

2

2

Выплата основного долга

3

процентах

3

процентах

Выплата основного долга

Остаток

4

4

Остаток

5

5

0

0

0,03*p=0,24

p = 8

Ответ: 8%

Задачи на вклады и инвестиции

Решение:

Задачи решаемые при помощи производной

• Антон является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном заводе трудятся суммарно t 2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, - 200 рублей. Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?

Задачи решаемые при помощи производной

• Строительство нового завода стоит 78 млн рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны 0,5х 2 +2x+6 млн рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит px-(0,5x 2 +2x+6). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более, чем за 3 года?

Решение:

• За 3 года прибыль составит:
• 3⋅(px−(0,5x²+2x+6)).
• Нужно найти наименьшее значение p, при котором выполнится неравенство:
• 3⋅(px−(0,5x²+2x+6))≥78
• px−(0,5x²+2x+6)≥26,
• px≥0,5x²+2x+32,
• p≥0,5x+2+32/x.

• Так как нужно найти наименьшее значение p, то нужно исследовать функцию 0,5x+2+32/x на минимум. Для этого найдем ее производную:
• (0,5x+2+32/x)′=0,5−32/x²,
• 0,5−32x²=0,
• x²=64, x1=8, x2=−8.
• x = 8 - точка минимума, поэтому минимальное значение p равно:
• p=0,5⋅8+2+32/8=4+2+4=10.
• Искомое наименьшее значение p = 10.

Ответ: 10

Критерии оценивания

Спасибо

за

внимание!

Интернет-ресурсы:

Школьный клипарт http://s3.pic4you.ru/allimage/y2013/10-24/12216/3925122.png

Линейки http://s1.pic4you.ru/allimage/y2012/08-20/12216/2356205.png

Лист в клеточку http://s1.pic4you.ru/allimage/y2012/08-20/12216/2356208.png

Скрепка http://img-fotki.yandex.ru/get/6610/134091466.1c/0_8f975_cc74afe5_S

Циркуль http://img-fotki.yandex.ru/get/6521/108950446.113/0_cd1e6_7c1b8dea_S

Открытый банк заданий ЕГЭ по математике

Образовательный портал для подготовки к экзаменам «РЕШУ ЕГЭ, МАТЕМАТИКА»

ЕГЭ 201 5 . Математика. Типовые тестовые задания / под ред. А.Л.Семенова, и.В.Ященко. – М.: Издательство «Экзамен»

Гущин Д. Д. Встречи с финансовой математикой