МАТЕРИАЛЫ ДЛЯ УСТНОЙ РАБОТЫ НА УРОКАХ АЛГЕБРЫ В 7 КЛАССЕ
- Устные тесты,
- устные упражнения;
- математические диктанты,
- развивающие таблицы.
Учитель Козина Н.А.
ВЫРАЖЕНИЯ
- Найдите значение выражения:
5
- 4
-1,5
-1
П1 Числовые выражения.
ВЫРАЖЕНИЯ
= 0,25
= 49
= - 0,001
П1 Числовые выражения.
-0 ,8
ВЫРАЖЕНИЯ
0 ,8
Р
В
4
Е
Т
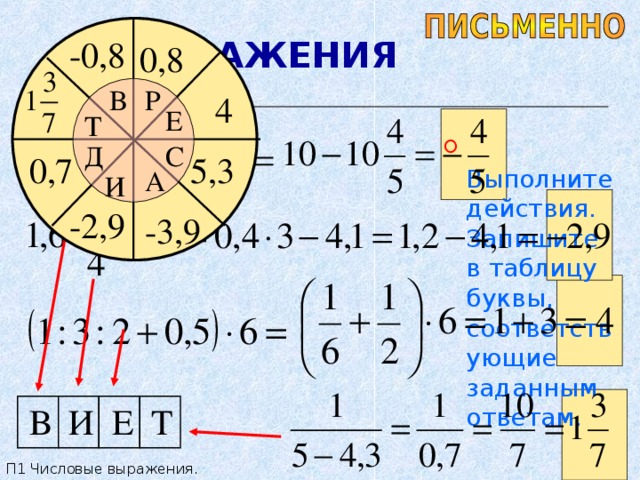
- Выполните действия. Запишите в таблицу буквы, соответствующие заданным ответам.
С
Д
5,3
0 ,7
А
И
-2,9
-3,9
В И Е Т
П1 Числовые выражения.
ВЫРАЖЕНИЯ
- - французский математик XVI века, который ввел систему алгебраических символов.
- Франсуа Виет был одним из первых, кто числа стал обозначать буквами.
П1 Числовые выражения.
ВЫРАЖЕНИЯ
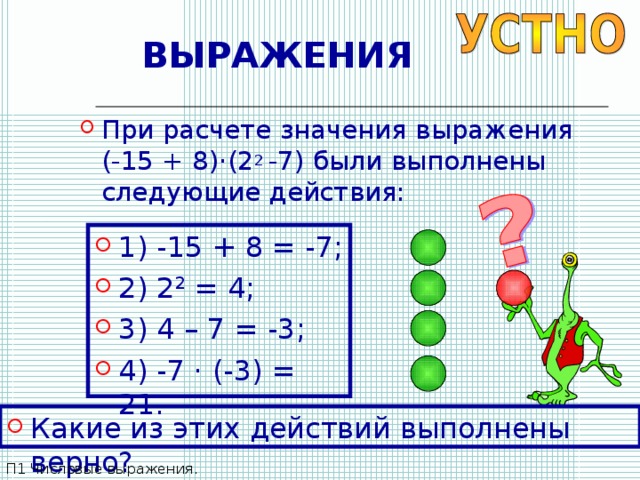
- При расчете значения выражения (-15 + 8) · (2 2 -7) были выполнены следующие действия:
- 1) -15 + 8 = -7;
- 2) 2 2 = 4;
- 3) 4 – 7 = -3;
- 4) -7 · (-3) = 21.
- Какие из этих действий выполнены верно?
П1 Числовые выражения.
ВЫРАЖЕНИЯ
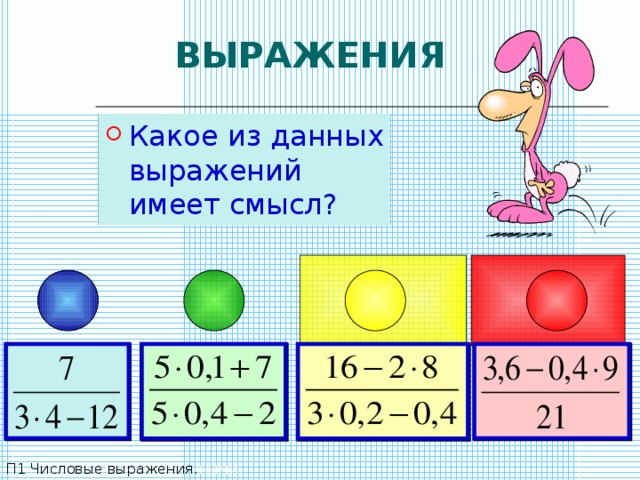
- Какое из данных выражений имеет смысл?
П2 Выражения с переменными.
П1 Числовые выражения.
ВЫРАЖЕНИЯ
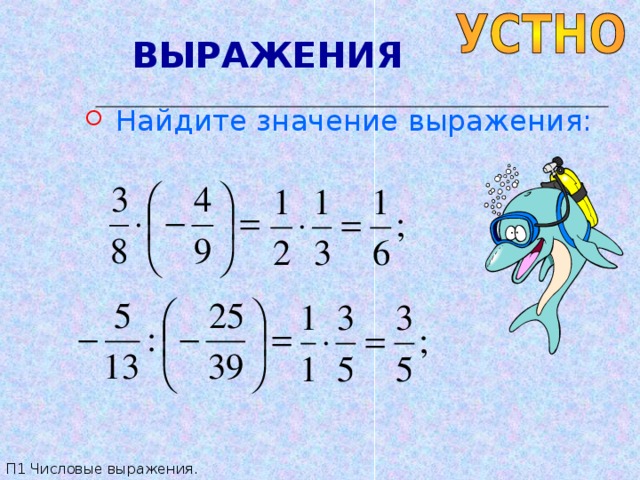
- Найдите значение выражения:
П1 Числовые выражения.
ВЫРАЖЕНИЯ
- Найдите значение выражения:
П1 Числовые выражения.
ВЫРАЖЕНИЯ
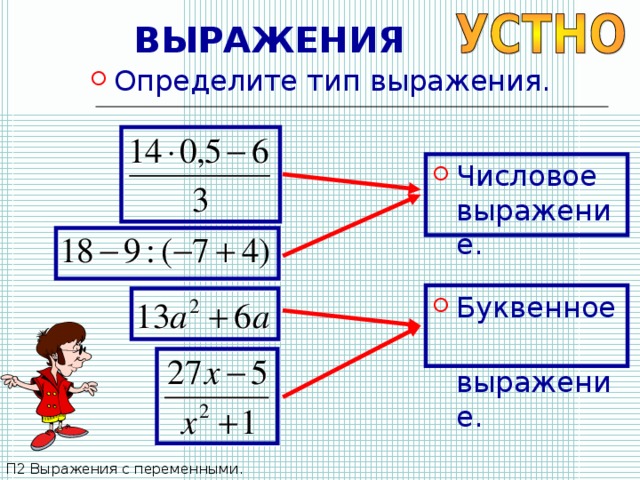
- Определите тип выражения.
выражение.
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- Известно, что a и b – стороны прямоугольника (в см). Какой смысл имеет выражение:
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- При некоторых значениях a и b значение выражения a – b равно 5. Какое значение при тех же a и b имеет выражение:
a - b
= 2
= 20
= -5
= 25
= 25
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- Найдите значение выражения x – y , если x = 1, y = 5.
6
4
-4
-6
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
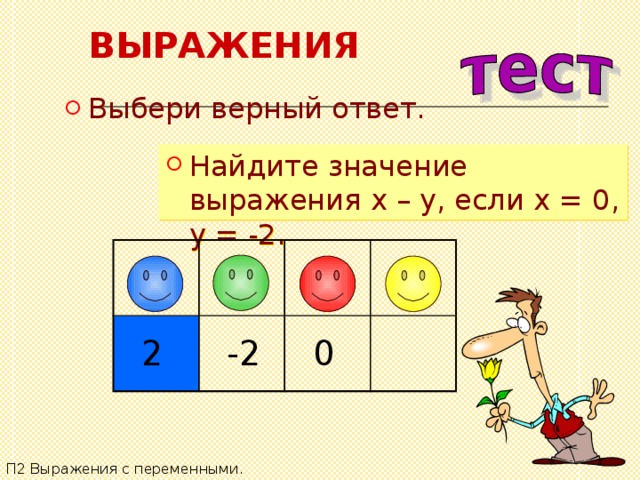
- Найдите значение выражения x – y , если x = 0, y = -2.
2
-2
0
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- Найдите значение выражения x – y , если x = -1,5, y = 0.
1,5
-1,5
0
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- При некоторых значениях a и b значение выражения a – b равно -5. Какое значение при тех же a и b имеет выражение:
b - a
= -1
= 5
= 25
a - b
= -0,2
= -125
= 51
4
= - 1,25
= -15
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- Дан прямоугольник со сторонами a и b . Укажите буквенное выражение, с помощью которого можно вычислить:
ab
a
2( a + b )
b
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- Дан прямоугольник со сторонами a и b . Укажите буквенное выражение, с помощью которого можно вычислить:
- Во сколько раз одна сторона больше другой:
a : b
a
- На сколько одна сторона меньше другой:
a - b
b
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- Дан прямоугольник со сторонами a и b . Укажите буквенное выражение, с помощью которого можно вычислить:
- Площади треугольников, на которые диагональ делит этот прямоугольник:
a
b
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- Дан прямоугольник со сторонами a и b . Укажите буквенное выражение, с помощью которого можно вычислить:
- Площадь оставшейся части, если из данного прямоугольника вырезали квадрат со стороной x :
a
x
ab – x 2
b
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- Дан прямоугольник со сторонами a и b . Укажите буквенное выражение, с помощью которого можно вычислить:
- Площадь заштрихованной фигуры:
a
x
b
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- Какому выражению соответствует высказывание?
- Выражение имеет смысл при всех значениях x , кроме x = 2.
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- Какому выражению соответствует высказывание?
- Выражение имеет смысл при всех значениях x , кроме x = 1 .
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- Какому выражению соответствует высказывание?
- Выражение имеет смысл при всех значениях x.
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- Площадь участка 160 га. В первый день вспахали 40% всей площади. Сколько гектаров осталось вспахать?
П3 Сравнение значений выражений. Повторение.
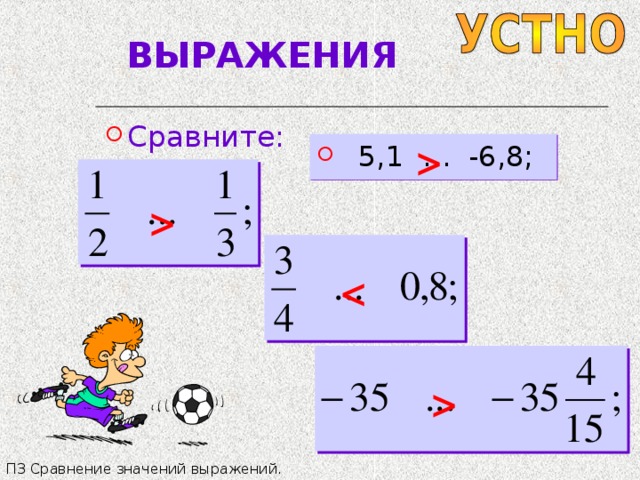5,1 … -6,8; П3 Сравнение значений выражений. " width="640"
ВЫРАЖЕНИЯ
П3 Сравнение значений выражений.
ВЫРАЖЕНИЯ
П3 Сравнение значений выражений.
П3 Сравнение значений выражений.
0 ,41 … ; (-3) 2 … -3 2 ; = (-1) 102 … 1; (-1) 103 … 1; П3 Сравнение значений выражений. П3 Сравнение значений выражений. " width="640"
ВЫРАЖЕНИЯ
=
П3 Сравнение значений выражений.
П3 Сравнение значений выражений.
-18 · 9,3 · (-5,2) … 0 ; (7,8 – 4,9) · (4,9 – 7,8) … 0; = -7 · (-6) · (-5) ·…· 5 · 6 … 0; П3 Сравнение значений выражений. П3 Сравнение значений выражений. " width="640"
ВЫРАЖЕНИЯ
- (7,8 – 4,9) · (4,9 – 7,8) … 0;
=
- -7 · (-6) · (-5) ·…· 5 · 6 … 0;
П3 Сравнение значений выражений.
П3 Сравнение значений выражений.
ВЫРАЖЕНИЯ
- Дано выражение
- Из предложенных вариантов выбрать те значения переменной x , при которых указанное выражение не имеет смысла.
2
-2
-3,5
3
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
- Дано выражение
- Из предложенных вариантов выбрать те значения переменной x , при которых указанное выражение не имеет смысла.
-3
-2,5
-9
3
П2 Выражения с переменными.
ВЫРАЖЕНИЯ
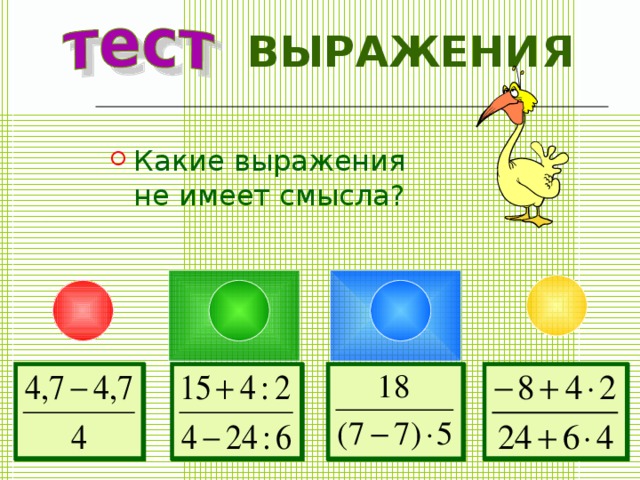
- Какие выражения не имеет смысла?
ВЫРАЖЕНИЯ
- Вычислите наиболее удобным способом:
19,9 ;
1,79 ;
- 2,3 · 0,098 + 2,3 · 0,002 =
= 2,3 (0,098 + 0,002) =
= 2,3 · 0,1 =
0,23
П4 Свойства действий над числами.
П3 Сравнение значений выражений.
ВЫРАЖЕНИЯ
- Вычислите наиболее удобным способом:
18 ;
П3 Сравнение значений выражений.
П4 Свойства действий над числами.
ВЫРАЖЕНИЯ
- Какое из чисел обращает неравенство -2,4 ≤ x ≤ -2 , 1
- в верное?
П3 Сравнение значений выражений.
П4 Свойства действий над числами.
ТОЖДЕСТВА
- Какие выражения являются тождеством?
- 5 x + 6 = 3x + 6 + 2x;
- 3(a+b) = 3a + b;
- 7a - (a-5) = 8a + 5;
- 7(x-y) = 7x – 7y.
П5 Тождества
ТОЖДЕСТВА
- Заполните пропуски в равенствах такими выражениями, чтобы они стали тождествами:
7x
12x
9a
5x
2x
5
П4 Тождества
П3 Сравнение значений выражений.
ТОЖДЕСТВА
- Заполните пропуски в равенствах такими выражениями, чтобы они стали тождествами:
a
c
- a + (b + c) = a + b + … ;
ac
1
0
a
П4 Тождества
П3 Сравнение значений выражений.
ТОЖДЕСТВА
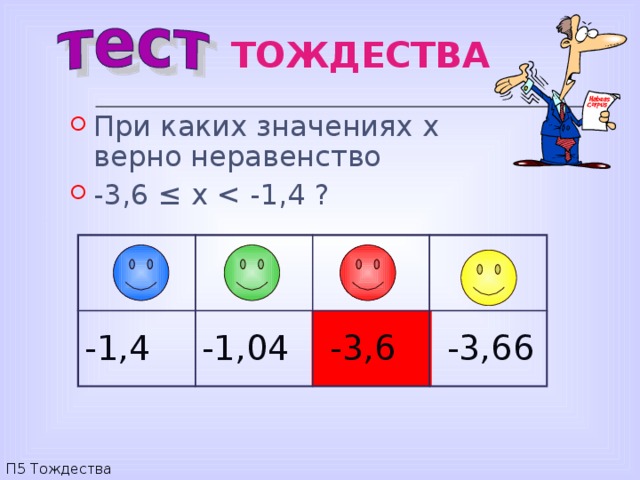
- При каких значениях x верно неравенство
- -3,6 ≤ x
-1,4
-1,04
-3,6
-3,66
П5 Тождества
ТОЖДЕСТВА
- Выбери верный ответ.
- -0,01 · 2,7
-270
-0,027
-0,27
0,027
Повторение
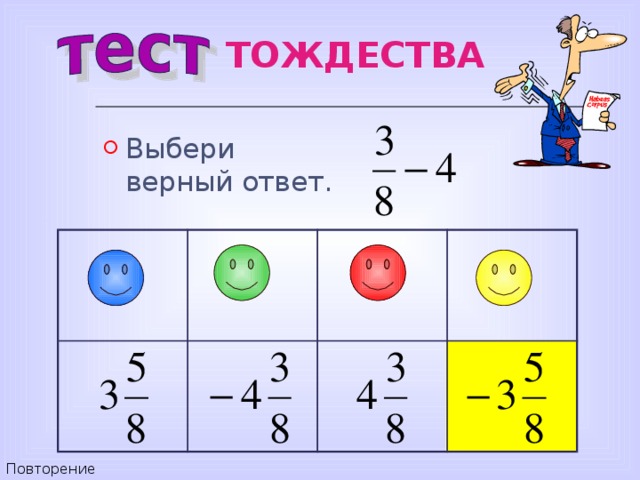
ТОЖДЕСТВА
Повторение
ТОЖДЕСТВА
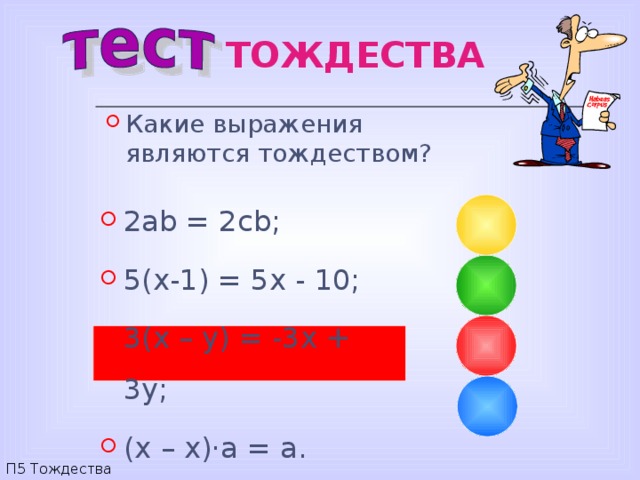
- Какие выражения являются тождеством?
- 2 ab = 2cb;
- 5(x-1) = 5x - 10;
- 3(x – y) = -3x + 3y;
- (x – x)·a = a.
П5 Тождества
ТОЖДЕСТВА
- Выбери верное высказывание.
- При x = 2 равенство верно ;
- При x = -0,7 равенство верно ;
- Равенство является тождеством ;
- При x = 0 равенство верно .
П5 Тождества
ТОЖДЕСТВА
- Выбери верное высказывание.
- Дано равенство x · x = x + x
- При x = 2 равенство верно ;
- При x = -0,7 равенство верно ;
- Равенство является тождеством ;
- При x = 0 равенство верно .
П5 Тождества
ТОЖДЕСТВА
- Выбери верное высказывание.
- Дано равенство x - 3x = -2x
- При x = 2 равенство верно ;
- При x = -0,7 равенство верно ;
- Равенство является тождеством ;
- При x = 0 равенство верно .
П5 Тождества
ТОЖДЕСТВА
- Выбрать выражения тождественно равные
- 3 x + x – 5y;
- 4x – (5y + x);
- -(5y – 4x);
- 3x – 4y + x + y.
П5 Тождества
ТОЖДЕСТВА
- Какое из равенств является тождеством?
- 5 x + 6 = 3x + 6 + 2x;
- 4(m – 2) = 4m – 2;
- 13x – (x + 5) = 12x + 5;
- 7a + (a – 5) = 8a - 5.
П5 Тождества
ТОЖДЕСТВА
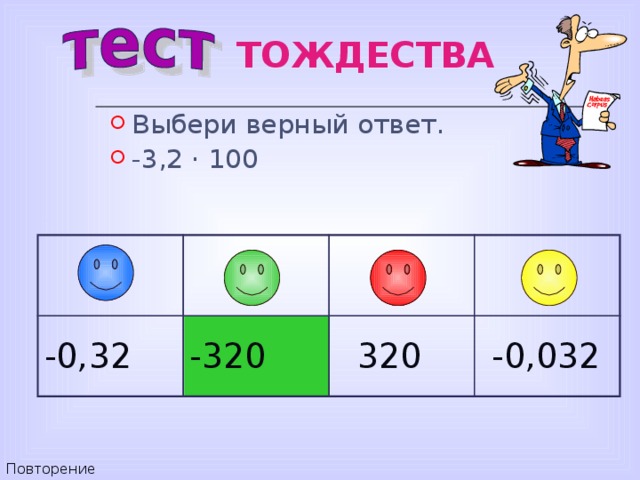
- Выбери верный ответ.
- - 3,2 · 100
- 0,32
- 320
320
- 0,0 32
Повторение
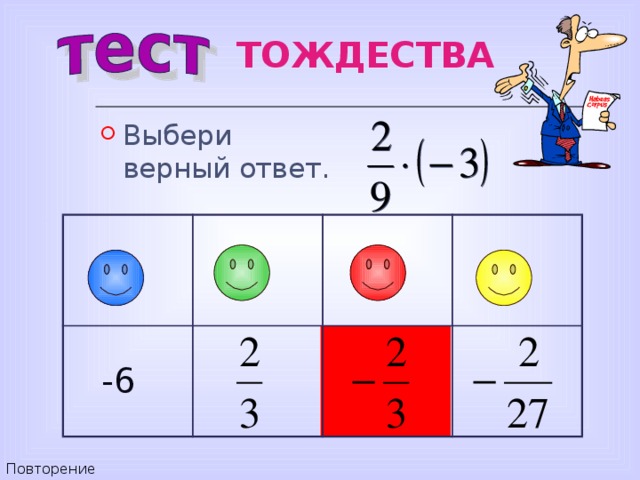
ТОЖДЕСТВА
-6
Повторение
ТОЖДЕСТВА
- Приведите подобные слагаемые:
- - a – 0,8a =
- b – b =
- -15c – 15a + 8a + 4c =
-1,8a;
-7a – 11c;
П6 Тождественные преобразования выражений
ТОЖДЕСТВА
- Раскройте скобки и приведите подобные слагаемые:
- -3 q – (8 p – 3q) =
- (2 + 3a) + (7a – 2) =
- 7p – 2(3p – 1) =
-3q – 8p + 3q =
– 8p;
2 +3a + 7a - 2 =
10a;
7p – 6p + 2 =
P + 2;
П6 Тождественные преобразования выражений
УРАВНЕНИЯ
- Выбрать записи, не являющиеся уравнением.
- 5 · 0,2 – 7 = -6 ;
- (x-1)(x+5) = 0;
- 4x - 9;
- 2x – 15 =3.
П7 Уравнение и его корни
УРАВНЕНИЯ
- Выбрать число, которое является корнем уравнения
- x 2 – x = 6 .
П7 Уравнение и его корни
УРАВНЕНИЯ
- Какие пары уравнений являются равносильными?
- 3x – 6 = 0; 3x = 6;
- 5(x+2) = 20; x+2 = 5;
- 5 + 2x = 5;
- 2x + 4 = 7; 5 + 2x = 2.
П7 Уравнение и его корни
УРАВНЕНИЯ
- Какие уравнения являются линейными?
- 3x = 7 ;
- x(x+2) = 0;
- 4x 2 – 5 = 19;
- 5x + 3 = 2x - 7;
П8 Линейное уравнение с одной переменной
УРАВНЕНИЯ
- Найдите корень уравнения:
а) 7 x = -14;
г) 3 x = 0;
б) - x = 4;
д)
│ · 5 .
в) 0,3 x = 9;
x = -5 .
П8 Линейное уравнение с одной переменной
УРАВНЕНИЯ
- Составьте какое – либо уравнение вида ax = b , корнем которого является число:
а) 3 ;
б) 0;
П8 Линейное уравнение с одной переменной
УРАВНЕНИЯ
- После решения линейного уравнения коэффициент при x оказался стертым. Восстановите его.
- 5 = ;
- x = -15 : 5 ;
- x = -3.
П8 Линейное уравнение с одной переменной
УРАВНЕНИЯ
- Какие уравнения имеют единственный корень?
- 4 x – 5 = 4 x;
- 2x = -0,06;
- 0,3x = 0;
- 5x + 2 = (5x – 4) +6;
П8 Линейное уравнение с одной переменной
УРАВНЕНИЯ
- Какие уравнения не имеют корней?
- 4 x – 5 = 4 x;
- 2x = -0,06;
- 0,3x = 0;
- 5x + 2 = (5x – 4) +6;
П8 Линейное уравнение с одной переменной
УРАВНЕНИЯ
- Какие уравнения имеют бесконечное множество корней?
- 4 x – 5 = 4 x;
- 2x = -0,06;
- 0,3x = 0;
- 5x + 2 = (5x – 4) +6;
П8 Линейное уравнение с одной переменной
УРАВНЕНИЯ
- Используя данные рисунка. Укажите алгебраическое выражение, с помощью которого можно узнать количество открыток у каждого из детей:
x открыток .
В 3 раза больше .
Коля .
3 x открыток .
Сева .
П9 Решение задач с помощью уравнений
УРАВНЕНИЯ
- Используя данные рисунка. Укажите алгебраическое выражение, с помощью которого можно узнать количество открыток у каждого из детей:
x открыток .
На 2 меньше .
Коля .
(x -2 ) открыток .
Лена .
П9 Решение задач с помощью уравнений
УРАВНЕНИЯ
- Используя данные рисунка. Укажите алгебраическое выражение, с помощью которого можно узнать количество открыток у каждого из детей:
x открыток .
Половина .
Коля .
0,5 x открыток .
Никита .
П9 Решение задач с помощью уравнений
УРАВНЕНИЯ
- Используя данные рисунка. Укажите алгебраическое выражение, с помощью которого можно узнать количество открыток у каждого из детей:
x открыток .
20% открыток .
Коля .
0,2 x открыток .
Маша
П9 Решение задач с помощью уравнений
УРАВНЕНИЯ
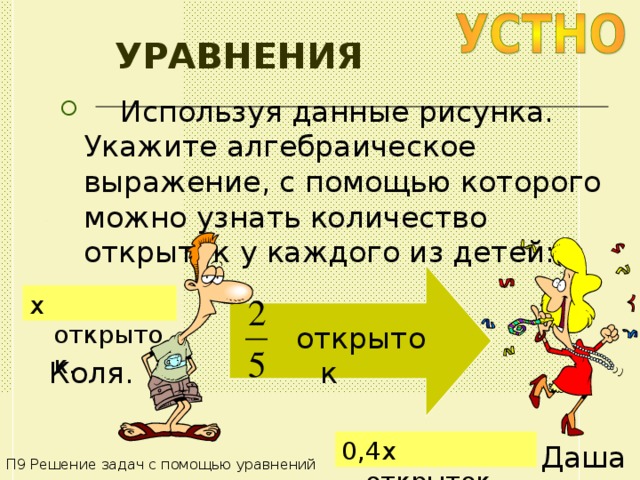
- Используя данные рисунка. Укажите алгебраическое выражение, с помощью которого можно узнать количество открыток у каждого из детей:
x открыток .
открыток
Коля .
0,4 x открыток .
Даша
П9 Решение задач с помощью уравнений
УРАВНЕНИЯ
- Используя данные рисунка. Укажите алгебраическое выражение, с помощью которого можно узнать количество открыток у каждого из детей:
x открыток .
На 20% меньше .
Коля .
0,8 x открыток .
Наташа
П9 Решение задач с помощью уравнений
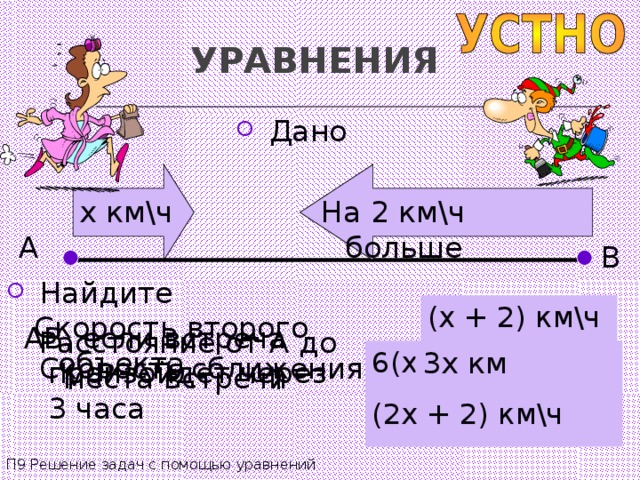
УРАВНЕНИЯ
x км\ч
На 2 км\ч больше
A
B
( x + 2) км\ч
Скорость второго объекта
AB , если встреча произойдет через 3 часа
Расстояние от А до места встречи
6 (x + 1 ) км
3 x км
Скорость сближения
(x + x + 2) км\ч
(2x + 2) км\ч
П9 Решение задач с помощью уравнений
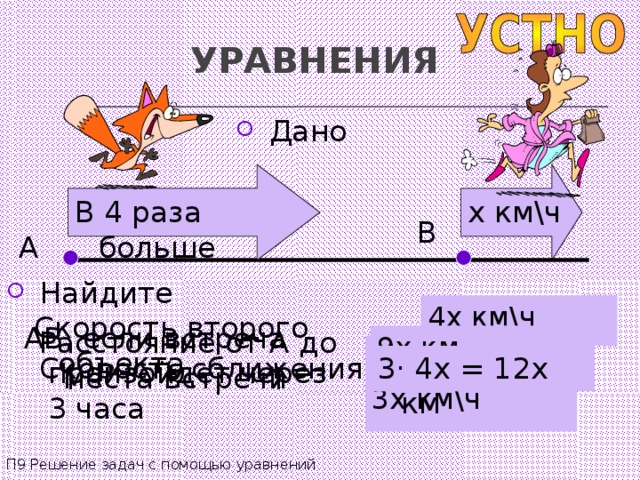
УРАВНЕНИЯ
В 4 раза больше
x км\ч
B
A
4 x км\ч
Скорость второго объекта
AB , если встреча произойдет через 3 часа
Расстояние от А до места встречи
9x км
4 x - x км\ч
3x км\ч
Скорость сближения
3 · 4x = 12x км
П9 Решение задач с помощью уравнений
Получите свидетельство
Вход
Выражения (2.63 MB)
0
813
141
Нравится
0
