Вычисление числа Pi с использованием вероятностных методов.

ТЕМА: Вычисление числа  с использованием вероятностных методов.

ЦЕЛЬ: Применение информационных технологий к решению инженерных и математических задач.

I . Определение площади круга и длины окружности. Число  как предел последовательности и отношение длины окружности к диаметру.

Вспомним, что мы знаем о числе .

Из курса школьной программы мы узнали, что отношение длины любой окружности к ее диаметру есть величина постоянная, равная примерно 3,14, и назвали ее . Из той же школьной программы мы узнали формулы длины(С=2R) и площади(S=R² )окружности радиуса R Доказательство этих формул проводится следующим образом:

1. вписываем в окружность правильный п-угольник и описываем около нее правильный п-угольник и станем неограниченно удваивать число их сторон;

2. составляем последовательности периметров и площадей этих многоугольников и выясняем, что эти последовательности сходятся, причем пределы последовательностей как периметров вписанных и описанных правильных многоугольников, так и их площадей соответственно равны.

3. При этом предел последовательностей периметров принимаем за длину окружности, а предел последовательностей площадей – за площадь круга.

4. При вычислениях мы получаем предел 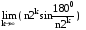, установим, что он должен существовать, так как длина окружности и площадь круга существуют и назовем его величиной .

Теперь формулы С=2R и S=R² доказаны, но значение числа  опять принимается нами на веру, так как 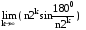мы еще не можем вычислить. Попробуем сделать это сейчас.

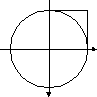
В С

Зная формулу площади круга радиуса R:

S_круга=R ² и формулу площади квадрата со стороной R:

S_{квадрата}=R² можно найти отношение этих площадей, О А х

что даст искомое значение числа .

Удобнее, однако, рассматривать не полный

круг, а его сектор радиуса R с прямым углом, который

вписан в квадрат ОВСА со стороной R. Тогда

S_{сектора}=0,25S_круга=0,25R² и S_{квадрата}=R²

Отношение S_{сектора}/S_{квадрата}=0,25, следовательно, для определения численного значения  достаточно найти вероятность попадания точки в сектор, если эта точка наудачу брошена в квадрат ОВСА.

С точки зрения математики, точка М(х;у) будет принадлежать квадрату ОВСА, если для ее координат выполняются неравенства 0хR, 0yR, и точка М(х;у) будет принадлежать сектору ОВА, если для координат точки выполняются неравенства х0, у0, х²+у² R². Таким образом, мы легко можем оценить место положения точки, но как ее бросить наудачу в квадрат?

Мы сможем это сделать с помощью информационных технологий.

III . Метод Монте-Карло и его использование в реализации модели.

Прежде чем решать задачу, определим понятие точки с точки зрения информатики. Информатика под точкой понимает пиксель экрана, который имеет только целые координаты и имеет для каждого монитора определенные размеры.

Конкретизируем задачу, взяв R=500 пикселей, чтобы рисунок уместился на экране и был хорошо виден.

Методом Монте – Карло называют численный метод решения задач, идея которого заключается в следующем. Если надо приближенно вычислить некоторую величину а, то надо придумать такую случайную величину в, что, получив и обработав множество её значений, можно получить величину, которая может быть принята в качестве искомой.

Проиллюстрируем идею метода на простом примере.

Пусть требуется определить площадь некоторой ограниченной фигуры.

Построим квадрат (в общем случае – прямоугольник), содержащий эту фигуру. Выберем n случайных точек, равномерно распределённых в квадрате, и обозначим через m количество точек, попавших внутрь фигуры. Ясно, что когда n достаточно велико, значение m пропорционально площади фигуры:

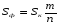(1)

Здесь S_ф и S_к — площадь фигуры и площадь квадрата соответственно.

Реализуем наши рассуждения на компьютере для решения задачи нахождения числа π.

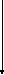y

.

. .

. .

. .

.

O x

1

Рассмотрим четверть круга единичного радиуса и описанный квадрат. Случайным образом выберем точки с координатами (x,y), такими, что 0 ≤ x ≤ 1 и 0 ≤ y ≤ 1.

Площадь четверти круга равна

, но r = 1, поэтому .

По формуле (1) 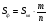, но S_кв=1, поэтому 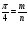, следовательно .

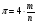Количество m точек, попавших внутрь четверти круга пропорционально его площади, т.е. π/4. Отношение (4m)/n, где n – число случайно выбранных пар координат, даёт, таким образом, приближённое число π.

Составим программу.

В Pascal’е имеется ДСЧ – функция Random(r:word). Если параметр r не задан, функция Random дает числа типа real из промежутка [0.0; 1.0), то есть только точки из квадрата. Кроме того, имеется процедура Randomize, которая инициализирует ДСЧ, т.е. меняет начальное значение. Количество точек, попавших в квадрат будем учитывать в цикле, что даст количество повторений. А для подсчета количества точек, попавших в сектор, организуем счетчик с критерием отбора x²+y²1.

Учитывая всё сказанное, напишем код.

Program E;

Var

N, k,i,j: long int:

X, y, b: real;

Begin

Writeln;

k:=0;

For i:=1 To 50 Do

Begin

Randomize;

For j:=1 To 10000 Do

Begin

x:=Random;

y:=Random;

If (x*x+y*y)

End;

N:=10000*i;

b:=(k/N)*4;

writeln(N:10,’ ‘,b:2:8)

end;

end.

Замечание. Так как квадратный корень из числа, меньшего 1, тоже меньше 1, мы здесь проверяем неравенство x²+y²≤1, хотя на самом деле надо проверять неравенство 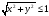. Таким образом, мы избежали использования функции Sqrt.

Вывод: В результате проектной работы мы получили программу для примерного подсчета числа 𝜋. Таким образом, с помощью информационных технологий, можно решить множество инженерных и математических задач.