Проект по информатике "Приближенное вычисление площадей фигур"

Цели: освоить понятие метода Монте-Карло, как основного метода создания вероятностных моделей; закрепить навыки работы в программной среде Pascal и в электронных таблицах Excel; активизировать творческие способности в ходе выполнения самостоятельного задания; актуализировать знания, полученные при изучении курса геометрии.

Задачи: уметь записывать предикат для фигуры, площадь которой необходимо найти; решить поставленную задачу используя среду программирования Pascal и электронные таблицы Excel; оформить решение в Word; сравнить полученные результаты.

Задание:

Применить метод Монте-Карло для приближенного вычисления площади фигуры.

Применить два способа построения компьютерной модели:

• построение алгоритма решения задачи на языке программирования Pascal;
• построение компьютерной модели с использованием электронных таблиц Excel .

Дети без труда напишут программу по данному алгоритму. И после этого наступает момент разочарования, сухие цифры. Поэтому, я предлагаю два способа решения задачи, которые наглядно демонстрируют работу метода Монте-Карло.

Метод статических испытаний или метод Монте-Карло

В математике для решения задач часто требуются математические модели. Одна из таких задач – вычисление площадей. Конечно для простейших фигур (прямоугольников, многоугольников, кругов) вычисление площади не составляет труда: надо в известные формулы подставить исходные данные. А как быть, если фигура имеет сложные формы? Итак, задача: Дана фигура сложной формы рис. 1. Вычислить её площадь.

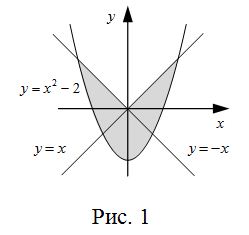
Поместим данную фигуру в квадрат. Будем наугад (как говорят математики, случайным образом) бросать точки в этот квадрат. Естественно, что чем больше площадь фигуры, тем чаще в неё будут попадать точки. Таким образом, можно сделать допущение: при большом числе точек, наугад выбранных внутри квадрата, доля точек, содержащихся в данной фигуре, приближенно равна отношению площади квадрата. Такой метод приближенного нахождения площадей фигур носит название метода Монте-Карло (по названию города, где расположена знаменитая рулетка, которую можно рассматривать как «генератор» случайных чисел).

Метод Монте-Карло:

1. Вписываем сложную фигуру в другую фигуру, для которой легко вычислить площадь. В нашем примере это квадрат (Рис. 2). Площадь квадрата S₀=16.
2. Равномерно разбрасываем N точек со случайными координатами внутри квадрата.
3. Подсчитываем количество точек, попавших на фигуру: M (записать предикат для точек с координатами (x, y), которые лежат внутри фигуры).  
4. Вычисляем площадь

Далее в документе показана программа на языке программирования Паскаль для вычисления площади фигуры по методу Монте-Карло.

II способ

(электронные таблицы Excel)

В Exсel имеется возможность проводить моделирование с использованием случайных чисел. Функция СЛЧИС( ) (без аргументов) генерирует случайное число в диапазоне от 0 до 1. Совокупность этих чисел равномерно распределена на отрезке [0; 1]. При нажатии функциональной клавиши F9 (пересчет) в ячейках, содержащих формулу с функцией СЛЧИС, генерируется новое случайное число.

Задания для самостоятельной работы:

1. Применить метод Монте-Карло для приближенного вычисления площадей фигур, представленных на рисунках.
2. Создать текстовый отчет по работе, включающий:
   • титульный лист (название работы, исполнитель);
   • постановку задачи и описание модели;
   • программу и результаты тестирования программы (I способ);
   • результаты, полученные в ходе выполнения задания в Excel (II способ);
   • качественный анализ результатов.
3. Организовать ссылки на файлы, реализующие метод Монте-Карло по I и II способу.

В архиве примеры заданий.