ГАПОУ «Оренбургский областной медицинский колледж»
Методическая разработка
для преподавателя
по дисциплине БД.04 МАТЕМАТИКА
«Введение в стереометрию»
Оренбург – 2020
Рассмотрено и одобрено
на заседании ПЦК
общеобразовательных дисциплин
Протокол № ___ от «__»_______
Председатель ПЦК
_________________ Н.В. Лапина
Автор:
Е.В. Данилова, преподаватель математики высшей квалификационной категории.
Аннотация:
Методическая разработка предназначена для преподавателей математики.
Содержит план занятия, конспект занятия, список источников информации.
В разработке предложены различные формы работы студентов и методы контроля знаний и умений по теме.
Содержание
| Технологическая карта занятия………………………………………………………. Ход занятия……………………………………………………………………………... Список источников…………………………………………………………………….. | 4 6 10 |
Технологическая карта занятия
Тема: Введение в стереометрию.
Вид занятия: теоретическое занятие.
Тип занятия: изучение нового.
Цели:
Образовательные:
Обучающийся научится:
оперировать на базовом уровне понятиями: точка, прямая, плоскость в пространстве;
изображать изучаемые фигуры от руки и с применением простых чертежных инструментов;
делать (выносные) плоские чертежи из рисунков простых объемных фигур: вид сверху, сбоку, снизу;
извлекать информацию о пространственных геометрических фигурах, представленную на чертежах и рисунках.
В повседневной жизни и при изучении других предметов:
соотносить абстрактные геометрические понятия и факты с реальными жизненными объектами и ситуациями.
Обучающийся получит возможность научиться:
Оперировать понятиями: точка, прямая, плоскость в пространстве;
применять для решения задач геометрические факты, если условия применения заданы в явной форме;
делать (выносные) плоские чертежи из рисунков объемных фигур, в том числе рисовать вид сверху, сбоку, строить сечения многогранников;
извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах, представленную на чертежах;
описывать взаимное расположение прямых и плоскостей в пространстве;
доказывать геометрические утверждения.
В повседневной жизни и при изучении других предметов:
использовать свойства геометрических фигур для решения задач практического характера и задач из других областей знаний.
Развивающие: Развивать память, логическое мышление, умение анализировать, проводить аналогии, делать выводы.
Воспитательные: Способствовать развитию потребности к самообразованию; саморазвитию. Воспитывать аккуратность и дисциплинированность.
Методическая: Ввести понятие стереометрии, рассмотреть основные фигуры и их комбинации, их обозначения и изображение.
Опорные понятия, термины: Стереометрия, точка, прямая плоскость, аксиомы стереометрии и следствия из них.
Межпредметные связи: физика, медицина, история.
Внутрипредметные связи: параллельность и перпендикулярность прямых и плоскостей, многогранники и тела вращения, векторы в пространстве.
Формы контроля: устный (фронтальный опрос), решение задач.
Методы: словесные, практические, наглядные, проблемные.
Оснащение:
Методическое: рабочая программа, тематическое планирование, ФГОС СОО, ПООП СОО, план занятия.
Дидактическое: учебник «Геометрия 10-11».
Литература: Геометрия 10-11 классы: базовый и профил. Уровни/ [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – М.: Просвещение, 2018г.
Оборудование: доска классная, мел, линейка, телевизор с USB.
Этапы занятия:
Организационный этап (1-2 мин).
Постановка цели и задач занятия. Мотивация учебной деятельности учащихся (2-3 мин).
Актуализация знаний (5-7 мин).
Изучение новой темы (60-65 мин).
Первичная проверка понимания (10-12 мин).
Рефлексия, подведение итогов занятия (2-3 мин).
Домашнее задание (1-2 мин).
План занятия
Организационный этап (1-2 мин).
Проверка готовности студентов к занятию. Проверка присутствующих.
Постановка цели и задач занятия. Мотивация учебной деятельности учащихся (2-3 мин).
Сообщение темы, целей, задач и плана занятия. Обоснование важности изучаемой темы.
Актуализация знаний (12-15 мин).
Фронтальный опрос на знание основных понятий планиметрии.
Изучение новой темы (55-60 мин).
Понятие стереометрии.
Основные фигуры, их изображение и обозначения.
Аксиомы стереометрии и следствия из них.
Первичная проверка понимания (7-10 мин).
Рефлексия, подведение итогов занятия (2-3 мин).
Домашнее задание (1-2 мин).
Стр. 3-7. №2,6.
Ход занятия
Актуализация знаний
Вопросы фронтального опроса:
Какие геометрические фигуры изучали в школьном курсе геометрии с 7 по 9 класс?
Какие из них являются основными?
Как они обозначаются и изображаются?
Где все изучаемые фигуры были расположены?
Как называется раздел геометрии, изучающий фигуры и их свойства на плоскости?
Где будут расположены объемные фигуры?
Какие первые утверждения были изучены в курсе геометрии?
Что такое аксиома?
Что такое теорема?
Изучение новой темы
Понятие стереометрии
Школьный курс геометрии состоит из двух частей: планиметрия и стереометрия.
Планиметрия – это часть геометрии, занимающаяся исследованием и измерением фигур на плоскости.
Стереометрия – это раздел геометрии, в котором изучаются фигуры и их свойства в пространстве.
Стереометрия — греческое слово. Оно произошло от слов "стерео" - тело и "метрио" - измерять, т.е. буквально стереометрия означает "теломерие". Стереометрия, как и планиметрия, возникла и развивалась в связи с потребностями практической деятельности человека. О зарождении геометрии в древнем Египте около 2000 лет до н.э. древнегреческий ученый Геродот (V в. до н.э.) писал следующее: "Сеозоострис, египетский фараон, разделил землю, дав каждому египтянину участок по жребию и взимал соответствующим образом налог с каждого участка. Случалось, что Нил заливал тот или иной участок, тогда пострадавший обращался к царю, а царь посылал землемеров, чтобы установить, на сколько уменьшился участок, и соответствующим образом уменьшить налог. Так возникла геометрия в Египте, а оттуда перешла в Грецию".
Одной из самых первых и самых известных школ была пифагорейская (VI-V вв.до н. э.), названная так в честь своего основателя Пифагора. Для своих философских теорий пифагорейцы использовали правильные многогранники, формы которых придавали элементам первооснов бытия, а именно: огонь – тетраэдр, земля - гексаэдр (куб); воздух – октаэдр; вода – икосаэдр; вся Вселенная, по мнению древних, имела форму додекаэдра.
Более поздняя философская школа – Александрийская – интересна тем, что дала миру знаменитого ученого Евклида, который жил около 300 г. до н. э. В его тринадцати книгах «Начала» впервые было представлено аксиоматическое построение геометрии. На протяжении около двух тысячелетий этот труд остается основой изучения систематического курса геометрии. Царь Птолемей спросил у Евклида, нельзя ли найти более короткий и менее утомительный путь к изучению геометрии, чем его "Начала". Евклид на это ответил: "В геометрии нет царского пути".
В последние столетия в геометрии появились новые методы, в том числе координатный и векторный, позволившие переводить геометрические задачи на язык алгебры и наоборот. Возникли и развиваются новые направления геометрических исследований: геометрия Лобачевского, проективная геометрия, топология, компьютерная геометрия и др. Геометрические методы широко используются в других науках: физике, химии, биологии,
Основные фигуры, их изображение и обозначения
Основными фигурами в пространстве являются точка, прямая и плоскость.
Плоскости изображаются в виде параллелограммов и обозначаются строчными греческими буквами: α, β, γ…
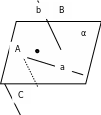
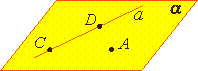
На рисунке изображены плоскость α, прямые а и b и точки А, В, С.
Про точку А и прямую а говорят, что они лежат в плоскости α или принадлежат ей.
А α, а α.
Про точки В и С и прямую b говорят, что они не принадлежат ей.
В α, С α, b α.
Аксиомы стереометрии и следствия из них
Введение основной геометрической фигуры – плоскости расширяет систему аксиом. Перечислим аксиомы, которые выражают основные свойства плоскостей в пространстве.
Эти аксиомы обозначают буквой А (с. 5-6 учебника).
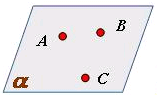
А1: Через любые три точки, не лежащие на одной прямой, проходит плоскость, и при чем только одна.
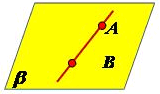
А2: Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости.
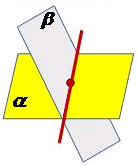
А3: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Используя эти аксиомы можно доказать несколько первых теорем стереометрии – простейшие следствия.
Т1: Через прямую и не лежащую на ней точку проходит плоскость, и при том только одна.
 (Доказать самостоятельно)
(Доказать самостоятельно)
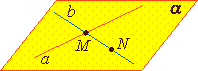
Т2: Через две пересекающиеся прямые проходит плоскость, и при том только одна.
 (Доказать самостоятельно)
(Доказать самостоятельно)
Просмотр обучающего видео.
Первичная проверка понимания
Выполнить чертеж:
а) Аα, Вα, С(АВ)
б) Аα, аα, Аа
в) аα=А, bα=А
г) аb=А, аα, bα
Решение задач из учебника № 1, 3, 7.
Задача 1 (рис. 8 учебника).
Решение.
а) PE ADB, MK DBC, ...;
б) DK∩ ABC = C, ...;
г) ABC∩ DCB = BC, ... .
Задача 3
г) Верно ли, что через любые три точки проходит плоскость, и притом только одна?
Решение.
У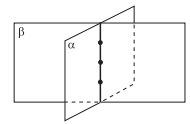 тверждение о том, что через любые три точки проходит плоскость, верно, но утверждение о единственности такой плоскости верно, только если заданные три точки не лежат на одной прямой. Если же заданные три точки лежат на одной прямой, то через эту прямую и, следовательно, через заданные три точки проходит бесконечное множество плоскостей.
тверждение о том, что через любые три точки проходит плоскость, верно, но утверждение о единственности такой плоскости верно, только если заданные три точки не лежат на одной прямой. Если же заданные три точки лежат на одной прямой, то через эту прямую и, следовательно, через заданные три точки проходит бесконечное множество плоскостей.
Задача 7
Дано: a∩ b =M, c ∩a = A, c∩ b = B, Mc.
Доказать: a, b, c лежат в одной плоскости. Лежат ли в одной плоскости все прямые, проходящие через точку M?
Р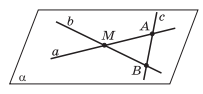 ешение.
ешение.
С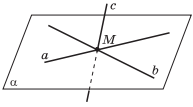 огласно второму следствию пересекающиеся прямые a и b определяют некоторую плоскость α. Точки A и B прямых a и b принадлежат плоскости α, следовательно, по аксиоме А2 прямая c лежит в плоскости α.
огласно второму следствию пересекающиеся прямые a и b определяют некоторую плоскость α. Точки A и B прямых a и b принадлежат плоскости α, следовательно, по аксиоме А2 прямая c лежит в плоскости α.
Если прямая c пересекает прямые a и b в точке M, то прямая c может лежать и может не лежать в плоскости α.
Домашнее задание
Стр. 3-7. №2,6.
Список источников
Геометрия 10-11 классы: базовый и профил. Уровни/ [Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.]. – М.: Просвещение, 2018г.
Интернет-ресурсы
http://school-collection.edu.ru/catalog/teacher/
http://www.school.edu.ru/

 Получите свидетельство
Получите свидетельство Вход
Вход











 Введение в стереометрию (102.88 KB)
Введение в стереометрию (102.88 KB)
 0
0 371
371 4
4 Нравится
0
Нравится
0








