Получите свидетельство
Вход
МБОУ Алтунинская ООШ
КОНСПЕКТ УРОКА ПО ГЕОМЕТРИИ 8 КЛАСС
Автор:
учитель математики
первой квалификационной категории
Рушева Т.Б.
Тема урока: Параллелограмм
Тип урока: урок изучения нового материала.
Цели урока: Формирование знаний свойств параллелограмма, умений строить параллелограмм, применять свойства параллелограмма при решении задач.
Оборудование и литература:
учебник (Геометрия, 7-9 классы. Атанасян Л.С.);
чертежные инструменты;
компьютер;
проектор;
экран.
План урока:
Организационный этап
Актуализация опорных знаний
Практическая работа «Построение параллелограмма»
Первичное усвоение новых знаний
Самостоятельная работа в группах по изучению свойств параллелограмма (через решение творческой работы)
Первичное закрепление
Постановка домашнего задания.
Подведение итогов
Ход урока
| Деятельность учителя | Деятельность учащихся | |
| Организационный момент | ||
| Учитель приветствует учащихся, проверяет готовность учащихся к уроку. | Приветствуют учителя. | |
| Актуализация опорных знаний | ||
| − Сформулируйте признаки равенства треугольников. | Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны. | |
| − Сформулируйте признаки параллельности прямых. | Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. Если при пересечении двух прямых секущей сумма односторонних углов =180 градусов, то прямые параллельны. | |
| − Сформулируйте свойство вертикальных углов. | «Вертикальные углы равны» | |
| − Какие вершины четырехугольника называются соседними? | «Вершины четырехугольника называются соседними, если они являются концами одной из его сторон» | |
| − Какие вершины четырехугольника называются противолежащими? | «Вершины, не являющиеся соседними, называются противолежащими» | |
| − Какие стороны четырехугольника называются соседними? | «Стороны четырехугольника, исходящие из одной вершины, называются соседними» | |
| − Какие стороны четырехугольника называются противолежащими? | «Стороны, не имеющие общего конца, называются противолежащими» | |
| − Что такое диагонали четырехугольника? | «Отрезки, соединяющие противолежащие вершины четырехугольника, называются диагоналями» | |
| Решение устных задач (на слайде) | Обдумывают 1-2 минуты, объясняют решение | |
| Практическая работа | ||
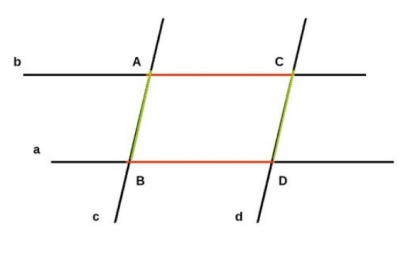
| Постройте прямую а, параллельную прямой b; Постройте прямую с, параллельную прямой d и пересекающие прямые а и b; Какие фигуры мы получили? (углы: вертикальные, смежные, соответственные, накрест лежащие, четырехугольник АВСД); Какие особенности можно указать у этого четырехугольника? Сделаем вывод.
Помогаем учащимся сформулировать тему урока. | Выполняют построение:
Делают вывод: мы получили четырехугольник, у которого противоположные стороны попарно параллельны. Формулируют тему урока.
| |
| Первичное усвоение новых знаний | ||
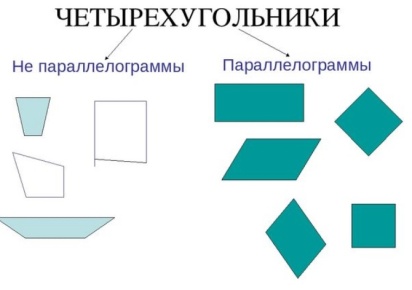
| Рассмотрим виды четырехугольников. Почему они разбиты на 2 колонки, сформулируем определение параллелограмма.
| записывают определение параллелограмма, выполняют чертеж. | |
|
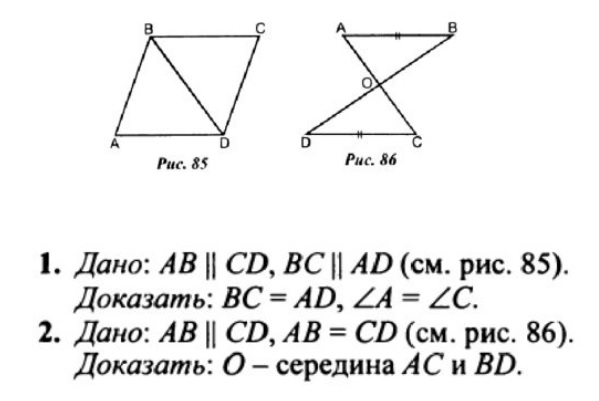
| В парах обсуждают задания, записывают решение в тетради и1 учащийся от каждого ряда выходит и решает на доске. (1 ряд – 1 задание, 2 ряд – 2 задание, 3 ряд – 3 задание) | |
| Самостоятельная работа в группах по изучению свойств параллелограмма | ||
| Предлагает в группах решить следующую задачу: Рассмотреть противолежащие углы, стороны и диагонали параллелограмма. Сформулируйте и докажите их свойства. - Что вы можете сказать о противолежащих углах и сторонах параллелограмма; - Что можно сказать о точке пересечения диагоналей параллелограмма? Учитель подходит к каждой группе, слушает высказывания учащихся, оказывает помощь. | учащиеся обсуждают решение данной задачи (могут пользоваться учебником) выбирают и готовят к выступлению делегата от группы. Каждая группа начинает свое выступление с формулировки свойства, с выделения условия и заключения. Делегат каждой группы приводит шаги доказательства и обоснование к ним, используя чертеж, делая записи на доске. Остальные учащиеся слушают, после чего вносят коррективы в ответ или исправление ошибок в решении у себя. | |
| Первичное закрепление (применение изученных свойств при решении задач) | ||
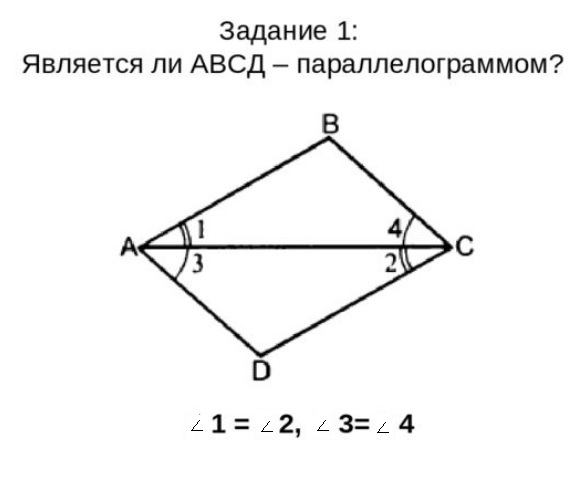
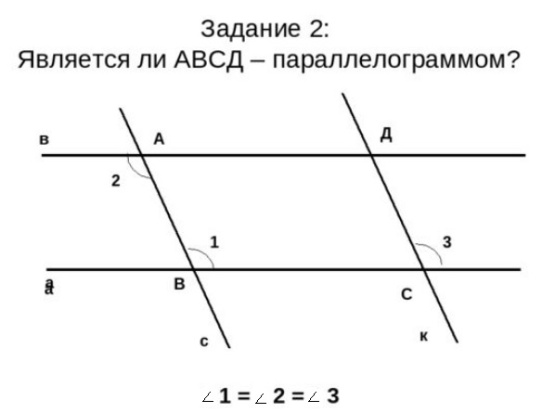
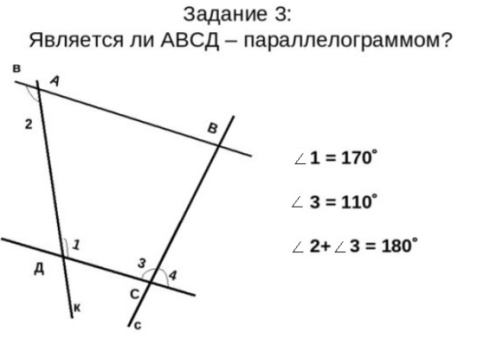
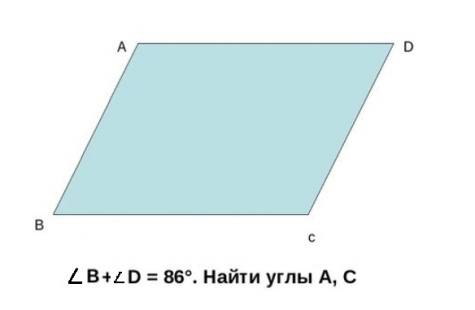
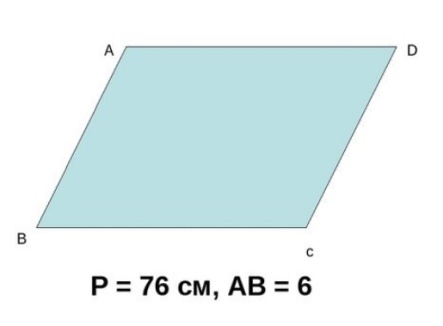
| Решение «устных» задач по готовым чертежам.
Учитель следит за ходом решения учащихся, направляет, корректирует решение. | Устно решают задачи, объясняют ход решения. | |
| № 376(а) Учитель следит за ходом решения учащихся, направляет, корректирует решение. № 372(а) | Решают в тетрадях и на доске. | |
| Постановка домашнего задания | ||
| Формулирует и комментирует ДЗ п. 43 ; № 372 (в); 376 (в, д). | Записывают ДЗ в дневник | |
| Подведение итогов
| ||
| Задает вопросы: Что такое параллелограмм? Сформулируйте свойства параллелограмма. Что было понятно/непонятно? Что было интересно? Что вызвало затруднения? | Отвечают на опросы, говорят что было понятно, непонятно, интересно, сложно и т.д. | |
|
|
| |
Уроки по теме "Параллелограмм" (214.99 KB)
0
85
3
Нравится
0
