Предмет: математика
Класс: 10
Тема урока: "Свойства выражений sin а и cos а"
Тип урока: комбинированный.
Цель урока: предполагается, что к окончанию урока учащиеся будут должны усвоить знания в их системе; уметь самостоятельно применять полученные знания, умения и навыки по данной теме, осуществлять их перенос в новые условия.
Задачи урока:
организовать выявление учащимися уровня своей компетентности по теме урока и устранение пробелов, создать условия ля полного усвоения знаний по данной теме..
создать условия для развития навыков самостоятельной работы, привития умения выслушивать других учащихся, дополнять их ответы, используя грамотно математические термины.
создать условия для усвоения учащимися свойства выражений
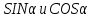 .
.создать условия для воспитания настойчивости, самостоятельности высказываний, точности и аргументированности высказываний, нацеленности учащихся на успех в учебной деятельности.
Оборудование: мультимедийный проектор, экран, ноутбук.
Дидактическое обеспечение: презентация, листы для проведения математического диктанта.
План урока:
Устная работа.
Математический диктант.
Объяснение нового материала.
Решение упражнений.
Это интересно.
Подведение итогов урока.
Ход урока.
Организационно-мотивационный этап
Цель этапа – создание условий для благоприятной психологической обстановки на уроке, подготовка учащихся к сознательному освоению учебного материала.
Здравствуйте, ребята! Я очень рада вас всех видеть и надеюсь на совместную плодотворную работу.
Французский писатель Анатоль Франс однажды заметил: «Учиться надо весело…Чтобы переваривать знания, надо поглощать их с аппетитом.» (слайд 1)
Так вот, давайте сегодня будем активны, внимательны, сообразительны, будем поглощать знания с большим аппетитом. Ну а кого на данный момент аппетит отсутствует, надеюсь, что он появится во время нашей работы, так как всем известно, что аппетит приходит во время еды.
Объявить тему урока (слайд 2), цели урока (слайд 3), план урока (слайд 4).
Операционно-познавательный этап.
Цель этапа – достижение учащимися цели урока.
2.1 Устная работа
Вопросы: 1. Дайте определение синуса угла 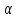 ? (слайд 5)
? (слайд 5)
2. Дайте определение косинуса угла 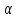 ? (слайд 5)
? (слайд 5)
3. Объясните, что это за отношение между градусной и радианной мерами угла.
(слайд 6)
4. Какие бывают углы поворота луча? (слайд 7), (слайд 8)
5. Назовите знаки синуса и косинуса по четвертям. (слайд 9)
6. Назовите промежутки знакопостоянства синуса и косинуса. (слайд 9)
7. Значения тригонометрических функций. (слайд 10)
Математический диктант (слайд 11)
Вариант 1
Сколько градусов в одном радиане?
В какой четверти оканчивается угол
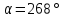 ?
?Выразите в градусах
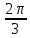 .
.Выразите в радианах 1400.
Вычислите cos 450.
Определите знак sin 2500.
Найдите величину угла смежного с углом
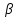 , равным
, равным 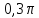 .
.Вычислите
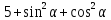 .
.Укажите все значения угла
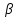 ,удовлетворяющие равенству
,удовлетворяющие равенству 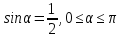 .
.Вычислите
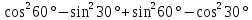 .
.
Вариант 2
Сколько радиан в одном градусе?
В какой четверти оканчивается угол
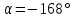 ?
?Выразите в градусах
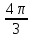 .
.Выразите в радианах 1500.
Вычислите sin 600.
Определите знак sin 2900.
Найдите величину угла смежного с углом
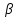 , равным
, равным 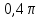 .
.Вычислите
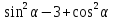 .
.Укажите все значения угла
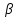 ,удовлетворяющие равенству
,удовлетворяющие равенству 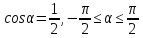 .
.Вычислите
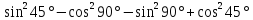 .
.
Проверка математического диктанта (слайд 12)
Собрать у ребят верхние листики с математическим диктантом, оставив им нижние копии для проверки.
Вариант 1.
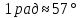 .
.3 четверть.
1200.
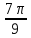 .
.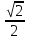 .
.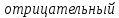 .
.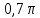 .
.6.
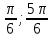
0.
Вариант 2.
.
3 четверть.
2400.
.
.
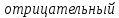 .
..
-2.
0.
РЕЛАКСАЦИЯ Ребята, мы с вами повторили основные моменты пройденных тем, написали математический диктант, проверили его, вы уже знаете приблизительно свои баллы за диктант. Впереди у нас новая тема, поэтому сначала вы немного отдохните.
(Звучит спокойная расслабляющая музыка). Сядьте, пожалуйста, удобно, обопритесь о спинку стула, положите руки на колени, посмотрите на экран (слайд 13)
Как прекрасна эта осенняя аллея! Закройте глаза и представьте себе, что вы идете по этой аллее, под вашими ногами тихо шуршат опавшие листья. Рядом с вами идет близкий вам человек, вы абсолютно счастливы…А теперь немного помечтайте…Получилось? Молодцы… Открываем глаза и приступаем к дальнейшей работе.
Объяснение нового материала (слайд 14)
Откройте тетради и запишите сегодняшнюю тему урока: «Свойства выражений »
Множество значений синуса и косинуса. (слайд 15)
Из определения синуса и косинуса следует, что для любого угла 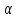 существует, и притом единственное, значение
существует, и притом единственное, значение (ордината точки
) и существует, и притом единственное, значение
(абсцисса точки
).
Точка лежит на единичной окружности, поэтому она может иметь любую абсциссу в пределах от -1 до 1 и никакой другой абсциссы иметь не может. А ее абсцисса - это
. Значит,
может принимать любое значение от -1 до 1 и никаких других значений принимать не может.
В частности, отсюда следует .
Аналогично доказывается, что может принимать любое значение от -1 до 1 и никаких других значений принимать не может.
В частности, отсюда следует .
Таким образом, множеством значений как синуса, так и косинуса является промежуток .
Четность и нечетность (слайд 16)
Точки и
единичной окружности ( при любом значении
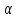 ) симметричны относительно оси ОХ, значит, ординаты этих точек – противоположные числа, а абсциссы – равные числа:
) симметричны относительно оси ОХ, значит, ординаты этих точек – противоположные числа, а абсциссы – равные числа: . По определениям синуса и косинуса имеем
.
Наибольшее и наименьшее значения синуса (слайд 17).
Из точек, лежащих на единичной окружности, наибольшую ординату, равную 1, имеет точка , то есть
принимает наибольшее значение при
.
Наименьшую ординату, равную -1, имеет точка , т.е.
принимает наименьшее значение при
.
Наибольшее и наименьшее значения косинуса (слайд 18).
Из точек, лежащих на единичной окружности, наибольшую абсциссу, равную 1, имеет точка , то есть выражение
принимает наибольшее значение при
.
Наименьшую абсциссу, равную -1, имеет точка , т.е. выражение
принимает наименьшее значение при
.
Нули синуса (слайд 19)
Ординаты, равные нулю, имеют те точки единичной окружности, которые лежат на оси Ох, т.е. и
. Итак,
при
и при
.
Обе эти группы значений 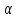 можно записать одной формулой
можно записать одной формулой
Эти значения называют нулями синуса.
Нули косинуса (слайд 20)
Абсциссы, равные нулю, имеют те точки единичной окружности, которые лежат на оси Оу, т.е. и
. Итак,
при
и при
.
Обе эти группы значений 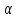 можно записать одной формулой
можно записать одной формулой
Эти значения называют нулями косинуса.
Контрольно-оценочный этап
Цель этапа – осознание учащимися результативности своей деятельности на уроке, уровня усвоения учебного материала.
Для закрепления свойства четность и нечетность тригонометрических выражений, решим №2.47(1,3,5) на стр.98
Для закрепления свойства множество значений синуса и косинуса решим
№2.58 на стр.106 устно
Может
Может
Не может
Не может
Может
Может
Не может
может
№2.66(нечет)
.
.
.
(Если позволит время, то решить №2.60(нечет))
Это интересно (слайд 21)
А сейчас, мы с вами будем разгадывать кроссворд.
Вопросы:
1. Раздел математики, изучающий свойства синуса и косинуса.(тригонометрия)
2. Абсцисса точки на единичной окружности. (косинус)
3. Синус – это … точки на единичной окружности. (ордината)
4. Отношение косинуса к синусу. (котангенс)
5. Косинусом угла
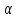 , называется … точки. (абсцисса)
, называется … точки. (абсцисса)
Итоги урока
Подведем итоги урока: мы пополнили словарный запас математического языка следующими терминами:
Область(множество) значений синуса и косинуса;
Четность и нечетность;
Наибольшее и наименьшее значения синуса и косинуса;
Нули синуса и косинуса.
При решении упражнений мы использовали лишь несколько из изученных сегодня свойств, с остальными свойствами будем работать на следующих уроках.
Информация о домашнем задании
Запишем домашнее задание (слайд 22). Объявить оценки за урок.
Рефлексия (слайд 23).
В завершении урока мне бы хотелось, чтобы каждый из вас оценил степень своего участия в уроке. Перед вами на экране таблица с забавными рожицами. Выберите себе, пожалуйста, тот рисунок, который, по вашему мнению, характеризует степень вашего участия. Выбрали? Молодцы! Мне хочется надеяться, что последний рисунок не выбрал никто.
Вы все сегодня очень хорошо потрудились. Спасибо за урок. До свидания!
3

 Получите свидетельство
Получите свидетельство Вход
Вход













 Урок по теме "Свойства выражений sin а и cos а" (43.63 KB)
Урок по теме "Свойства выражений sin а и cos а" (43.63 KB)
 0
0 505
505 21
21 Нравится
0
Нравится
0


