Урок по теме: «Теория вероятностей».
Организационная информация
Тема урока: «Введение в теорию вероятностей».
Предмет: ЕН.01 Математика.
Разработчик: Ахметова Гюзаль Абдрауфовна, преподаватель математики, информатики.
Образовательное учреждение: ГБПОУ «Уфимский лесотехнический техникум» г. Уфа
Группа: 101 ТЭМ
Тип урока: изучение нового материала.
Цели урока: изучить элементы теории вероятности, рассмотреть алгоритмы решения задач на заданную тему.
Задачи урока:
образовательные: изучить термины теории вероятностей: достоверные, невозможные, равновероятностные, противоположные, совместные и несовместные события; научить решать задачи из жизни, формирование вероятностного мышления.
воспитательные: воспитание умения слушать и вести диалог,
активно участвовать в коллективном обсуждении проблем.
развивающие: способствовать развитию интереса к математике; умений применять новый материал на практике и в жизни, контроль и оценка процесса и результатов деятельности, выбор наиболее эффективных способов решения задач в зависимости от конкретных условий, контроль и оценка процесса и результатов деятельности.
Социальные: профилактика приобщения молодежи к азартным играм, игровой зависимости.
Оборудование к уроку: компьютер с проектором, раздаточный дидактический материал, доска, презентация по теме «Введение в теорию вероятностей», шестигранные карандаши с пронумерованными гранями, игральные кубики, монеты, урна с шарами различных цветов.
План урока:
1.Организационный момент.
2. Вводное слово преподавателя. Постановка темы, цели, задач урока.
3.Изучение нового материала.
3.1. Групповая работа. Решение задач и проведение экспериментов.
3.2. Отчет каждой группы о проделанной работе. Выводы
Социальная проблема – Порок мира взрослых -Азартные игры
Домашние задание.
Подведение итогов урока.
Ход урока:
Организационный момент.
Приветствие класса. Отметка в журнале отсутствующих учащихся. Сообщение темы урока и формирование его целей.
Вступительное слово преподавателя.
Начнем урок с проблемных задач
Задача 1.
Студент при подготовке к экзамену не успел выучить один из тех 30 билетов, которые будут предложены на экзамене. Какова вероятность того, что студенту достанется на экзамене выученный билет?
Кому не случалось идти на экзамен с одним и более не выученными билетами?
При этом каждый из нас задавался вопросом: повезет или нет?
Скоро вы как студенты и можете попасть в такую же ситуацию. Как вы считаете, что надо применить для решения этой задачи? Встречались ли вы раньше с такого рода задачами? Где? Когда? Что вы помните из изученного раньше? Приведите примеры таких задач из своего жизненного опыта. /Учащиеся приводят примеры/.
Задача 2. Покупая лотерейный билет или играя в игровые автоматы, задумываемся ли мы о том, какова вероятность выигрыша?
Кто чаще выигрывает: игрок или казино? Можно ли выиграть у компьютера?
На эти вопросы мы постараемся ответить с помощью науки Теория Вероятностей.
Так вот, чтобы помочь студенту, научиться решать задачи по теории вероятностей и успешно сдать экзамен по математике за курс основной школы, необходимо обновить свои знания и изучить этот раздел математики
Задача 3. К примеру сегодня в аудитории отсутствует один из учащихся в связи с болезнью. А как вы думаете, можно ли при помощи математики предположить придет ли ученик на занятие или нет.
На этот вопрос ответит нам раздел математики – теория вероятности.
Изучение нового материала.
3.1 История возникновения теории вероятностей.
Теория вероятностей – раздел математики, изучающий закономерности случайный явлений: случайные события, случайные величины, их свойства и операции над ними.

Вы очень часто сталкиваетесь со случаем. Случайно достали не ту вещь из сумки, случайно открыли книгу на 55 станице, случайно столкнулись со знакомым на отдыхе в другой стране. Все это случайные события.
Как наука теория вероятности зародилась в 17в. Возникновение понятия вероятности было связано как с потребностями страхования, получившего значительное распространение в ту эпоху, когда заметно росли торговые связи и морские путешествия, так и в связи с запросами азартных игр (орлянка, кости, рулетка).
Честь открытия этой теории, которая не только даёт возможность сравнивать случайные величины, но и производить определенные математические операции с ними, принадлежит двум выдающимися ученым - Блезу Паскалю и Пьеру Ферма.

Но первый кто опубликовал свои размышления по теории вероятности, оказался Христиан Гюйгенс.

При этом с перепиской Паскаля и Ферма он знаком не был, поэтому методику решения изобрёл самостоятельно. Во второй половине 19 века основной вклад внесли русские учёные П. Л. Чебышев и А. М. Ляпунов. В это время были доказаны закон больших чисел центральная предельная теорема, а также разработана теория цепей
Маркова.

Современный вид теория вероятностей получила благодаря аксиоматизации предложенной Андреем Николаевичем Колмогоровым.

результате теория вероятностей приобрела строгий математический вид и окончательно стала восприниматься как один из разделов математики. сейчас мы послушаем доклад посвященный Андрею Николаевичу Колмогорову (один из студентов на предыдущем уроке вызвался подготовить данный доклад ).
Доклад студента о А.Н. Колмогорове (Юсупов Руслан, 101 ТЭМ).
Андрей Николаевич Колмогоров – выдающийся русский советский математик, один из основоположников современной теории вероятностей.
Андрей Николаевич родился 12 апреля 1903 г. в Тамбове. Мать Колмогорова - Мария Яковлевна, умерла при родах. Отец - Николай Матвеевич, погиб в 1919 г. во время Деникинского наступления.
Уже в раннем детстве мальчик проявлял недюжинные математические способности. В 1918 г. он поступил на математическое отделение Московского университета, а научные труды стали публиковаться когда автору исполнилось 20 лет.
В 1925 г. Колмогоров окончил университет и остался в его стенах как преподаватель. В 1930 г. он получил звание профессора, в 1935 г. защитил докторскую диссертацию, а в 1939 г., в возрасте 36 лет, был избран академиком.
В теории вероятностей А.Н. Колмогоров был признанным главой науки во всем мире. В 1933 г. он написал работу «Основные понятия теории вероятностей», которая была издана в Берлине на немецком языке, а затем переведена на русский язык в 1936 г. Она определила пути развития теории вероятностей. Классическая монография А.Н. Колмогорова «Теория вероятностей и математическая статистика», в которой он изложил современное состояние этого раздела математики, была издана в 1986 г.
Особым вкладом Колмогорова в развитие советской математики стало создание им научной школы в области теории вероятностей и теории функций. Академик воспитал не один десяток замечательных математиков - А.И. Мальцева, М.Д. Миллионщикова, С.М. Никольского, Ю.В. Прохорова, А.М. Обухова, А.М. Яглома, В.М. Тихомирова, И.М. Гельфанда и др.
Также Андрей Николаевич прославился грандиозной реформой школьного математического образования в 1960-е гг. Проведенная по инициативе и под руководством Колмогорова, реформа сделала советское математическое образование населения лучшим в мире.
Заслуги учёного перед наукой были отмечены многочисленными наградами: Государственная премия (1941 г.), Ленинская премия (1965 г.), 6 орденов Ленина, орден Трудового Красного Знамени, международная премия Больцано (1963 г.) и др. Андрей Николаевич состоял почётным членом академий наук Франции, Нидерландов, Польши, Румынии, США, Лондонского королевского общества.
А. Н. Колмогоров скончался 26 октября 1987 года. Он является автором свыше 500 научных работ в различных областях математики.
3.2 Определение понятия события. Виды событий.
Как вы уже поняли, теория вероятностей изучает случайные события. Так что же такое событие с точки зрения математики.
теории вероятностей под событием понимают то, относительно чего после некоторого момента времени можно сказать одно и только одно из двух:
Да, оно произошло.
Нет, оно не произошло.
Запишем:
Событие – это результат испытания.
Например, возьмем урну и в нее поместим шары различных цветов. Кто хочет извлечь из урны один шар (экспериментирует учащийся)? Извлечение шара из урны есть испытание. Появление шара определенного цвета – событие.
Из нашего опыта делаем вывод, что мы не можем с точностью определить шар какого цвета, мы вытянем из урны, не зная количество шаров разных цветов.
Кто может привести пример испытание и указать в нем событие (ответы учащихся).
жизни мы сталкиваемся с различными событиями – хорошими или плохими. Так и в теории вероятностей существуют различные виды событий.
Запишем подзаголовок: «Виды событий».
И запишем первый вид событий:
Случайные события.
жизни мы постоянно сталкиваемся с тем, что некоторое событие может произойти, а может и не произойти. Такие события в теории вероятности называют случайными.
Например: Книга откроется на 55 странице, при бросании игральной кости выпадет 6 очков.
У вас на партах лежат шестигранные карандаши, у которых грани пронумерованы, давайте бросим их и посмотрим, какое количество очков у вас выпадет (результаты испытания записываем на доске). Как вы видите, количество очков выпадает непредсказуемо.
Запишем еще два вида событий:
Совместные события.
Не совместные события.
Два события, которые в данных условиях могут происходить одновременно, называются совместными, а те, которые не могут происходить одновременно, - несовместными.
Если подбросить одновременно монету и игральный кубик, то выпадения орла на монете и 4 очков на кубике не мешают друг другу – они совместные.
Рассмотрим еще один пример: у вас на парте так же лежит монета, подкиньте ее. Как вы видите появление орла, исключает появление решки.
Как вы уже успели заметить в появлении орла или решки нет преимуществ.
Как бы мы не кидали, выпадет либо орел, либо решка.
Давайте запишем следующие виды событий:
Равновозможные события.
Не равновозможные события.
Равновозможными называются события, когда в их наступлении нет преимуществ.
Не равновозможные события те, у которых в наступлении одного из событий есть какое то преимущество.
Представьте, если бды у вас в руках находилась монета, у которой на двух сторонах изображена решка и появиться орел, при бросании монеты, ни как не может. Таким образом, фокусники и мошенники обманывали в 17 веке простых горожан.
Далее мы будем работать с равновозможными событиями.
Равновозможные события бывают:
1.Достоверными.
Событие, которое происходит всегда, называют достоверным (истинным) событием.
Невозможными.
Событие, которое не может произойти, называется невозможным (ложным).
Примеры.
Достоверные события:
Вы находитесь сейчас на уроке математики.
Сегодня на календаре месяц март.
Является ли достоверным событием что, вы сегодня позавтракали? Нет - это случайное событие.
Ложные события:
Ночью взойдет солнце.
Вы поедете на зимние олимпийские игры в Сочи.
Приведите примеры истинных и ложных событий.
Запишем в тетрадь:
Вероятность истинного события равна 1, а вероятность ложного события равна 0.
Если из корзины с синими и красными шарами вынимаю зеленый шар это ложное событие и его вероятность равна нулю. А если же из корзины со всеми белыми шарами я вынимаю белый шар это истинное и его вероятность равна единице.
3.3 Самостоятельная работа учащихся.
Решение задач в группах.
А теперь перейдем к работе в группах. Разделимся на 3 группы. Ваша задача: решить задачи, оформить их в тетрадях, провести эксперимент и рассказать о проделанной совместной работе. Листочки с заданиями, таблицы и материалы для экспериментов на столах.
На листах написаны события. Под событиями расположена таблица. И для каждого из перечисленных событий определяете, каким данное будет являться: достоверное, возможное, невозможное. Ответы отмечаем в таблице. В восьмом задание вы должны сами придумать событие и определить, какое это событие.
Раздаточный материал:
Задача 1.
Ф.И.О._______________________________________________________
Для каждого из перечисленных событий определите, какое оно:
достоверное, возможное, невозможное:
Солнце кружится вокруг Земли;
Ваше участие в летних олимпийских играх;
3.Вы выиграли в викторине;
4.В 9-м классе школьники не будут изучать геометрию;
мама старше своих детей;
6.вам за урок поставят оценку «4»;
7.Параллельные прямые не пересекаются.
| Событие | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Достоверное |
|
|
|
|
|
|
|
|
| Возможное |
|
|
|
|
|
|
|
|
| Невозможное |
|
|
|
|
|
|
|
|
Поменяйтесь с соседом по парте заданиям. И давайте проверим верность выполненного задания. После проверки оцените работу.
Задача 2. Из 20 учащихся класса двое справляют день рождения: 1). 30 января; 2). 30 февраля. Определите, каким является каждое из событий: невозможным, достоверным, или случайным.
Решение:1). Событие, заключающееся в том, что двое из 20 учащихся родились 30 января – случайное, оно может произойти, а может и не произойти (все зависит от состава группы из 20 учеников).
2). Второе событие – невозможное, поскольку даты 30 февраля не существует, следовательно, никто из учащихся не мог родиться в такой день.
Ответ: 1). Случайное, 2). Невозможное.
Задача 3. Из событий:
1). «идет дождь»;
2). «на небе нет ни облачка»;
3). «наступило лето»
– составить среди них пары совместимых и пары несовместимых.
Р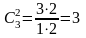 ешение. Из трех событий можно образовать 3 различных пары (порядок событий в паре значения не имеет); количества пар равно
ешение. Из трех событий можно образовать 3 различных пары (порядок событий в паре значения не имеет); количества пар равно
Это: 1). – 2). ; 1). – 3). ; 2). – 3).
События в 1 паре несовместные, во 2 паре – совместные, в 3 – совместные.
Ответ: 1 пара несовместных и 2 пары совместных событий.
Задача 4. Охарактеризуйте событие, о котором идет речь, как достоверное, невозможное или случайное. Вы открыли эту книгу на любой странице и прочитали первое попавшееся существительное. Оказалось, что:
В написании выбранного слова есть гласная буква
В написании выбранного слова есть буква «О»
В написании выбранного слова нет гласных букв
В написании выбранного слова есть мягкий знак.
Решение:
а). Событие достоверное, т.к. в русском языке нет существительных состоящих только из согласных букв.
b). Событие случайное.
c). Событие невозможное (см. а)
d). Событие случайное.
Ответ: a). Достоверное, b). Случайное, с). Невозможное, d). Случайное.
3.4 Классическое определение вероятности. Алгоритм решения задач.
Для того что бы решать данные задачи нам необходимо знать классическое определение теории вероятности.

Запишите подзаголовок: Классическое определение вероятности.
Вероятностью события А при проведении некоторого испытания называют отношение числа исходов благоприятных событию N(А), к общему числу всех (равновозможных между собой) исходов этого испытания N.
Запишем формулу:
| P( A) | N A |
|
| N |
| |
|
|
|
![]()
где:
P A вероятность события А;
N A благоприятные исходы события А;
все исходы.
Кто может повторить данную формулу?
Для решения задач используют алгоритм нахождения вероятности случайного события.
Для нахождения вероятности случайного события А при проведении некоторого испытания следует найти:
1)число N всех возможных исходов данного испытания;
2)количество N(A) тех исходов, в которых наступает событие А;
3)частное
| N ( A) | ; |
|
| N |
| |
|
|
|
![]()
оно и будет равно вероятности события А.
Принято вероятность события А обозначать так: Р(А).
Значит Р(А) = N ( A) .
N
Пример 1:
В соревновании по толканию ядра участвуют 4 спортсмена из России, 9 спортсменов из Белоруссии, 7 спортсменов из Грузии и 5 – из Словении. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из России?
Решение: Всего спортсменов принимающих участия в соревнования – 25, а спортсменов из России – 4. Исходя из нашего алгоритма, получаем что:
N(A) = 4;
N= 25
P ( A) 254 0,16
Ответ: 0,16.
Вероятность события выражается в виде десятичной дроби и в процентах.
Нам необходимо выражать вероятность события в виде десятичной дроби.
Для вычисления вероятности часто используют правило умножения.
вас на партах лежат две игральные кости. Пусть один из вашей пары возьмет две игральные кости и подкинет их. Выпало определенное количество очков, запомните их. Как вы думаете, сколько всего исходов данного события, сколько очков может выпасть на двух игральных костях?
Всего таких исходов 6*6 – на первой кости может выпасть шесть различных вариантов и на второй игральной кости тоже шесть.
Для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А и число всех исходов испытания В.
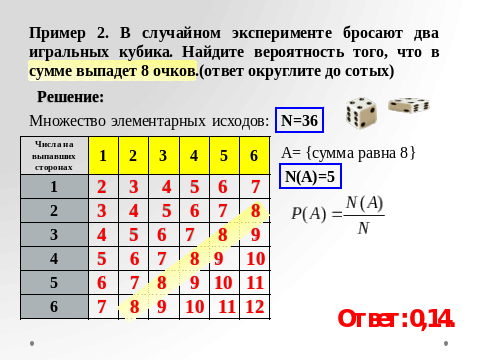
Пример 2.
случайном эксперименте бросают два игральных кубика. Найдите вероятность того, что в сумме выпадет 8 очков (ответ округлите до сотых).
Решение. Игральные кости - это кубики с 6 гранями. На первом кубике может выпасть 1, 2, 3, 4, 5 или 6 очков. Каждому варианту выпадения очков соответствует 6 вариантов выпадения очков на втором кубике. Т.е. N = 6×6 =
Варианты (исходы эксперимента) будут такие:
1;1 1;2 1;3 1;4 1;5 1;6
2;1 2;2 2;3 2;4 2;5 2;6 и т.д. ..............................
6;1 6;2 6;3 6;4 6;5 6;6
Подсчитаем количество исходов (вариантов), в которых сумма очков двух кубиков равна 8: 2;6 3;5; 4;4 5;3 6;2…. Всего N(A) = 5 вариантов. Найдем вероятность.
| P ( A) | 5 | 0,138... | 0,14 |
|
| 36 |
| |||
|
|
|
|
|
![]()
Ответ: 0,14.
При решении некоторых задач удобно использовать свойство вероятностей противоположных событий.
Запишем подзаголовок: Свойства противоположных событий.
События А и В называются противоположными, если всякое наступление события А означает не наступление события В, а не наступление события А – наступление события В.
Например: Если выпадет на монете орел, решка не выпадет.
Событие, противоположное событию А, обозначают символом А .
Вероятность Р(А) некоторого события 0 Р( А) 1.
Свойство противоположных событий:
Сумма вероятностей противоположных событий равна 1.
Р( А) Р( А)
![]()
1
.
Пример 3.
Бросаем один раз игральную кость. Событие А – выпадение четного числа очков, тогда событие А - выпадение нечетного числа очков
![]()
Пример 4.
В среднем из 1000 аккумуляторов, поступивших в продажу, 6 неисправны. Найдите вероятность того, что один купленный аккумулятор окажется исправным.
Решение. Элементарный исход – случайно выбранный аккумулятор. Поэтому
N = 1000.
Событию А = {аккумулятор исправен} благоприятствуют 1000 – 6 = 994 исхода.
Поэтому N(A) = 994.

Тогда
| Р(А) | N(A) | | 994 | 0,994. |
|
| N | 1000 |
| |||
|
|
|
|
|
![]()
Ответ: 0,994.
Эту задачу можно решить с помощью формулы вероятности противоположного события А = {аккумулятор неисправен}. Тогда N(Ā)=6.
![]()
Имеем
P( A )
![]()
=
| N ( A) | 0,006. |
|
| N |
| |
|
|
|
![]()
![]()
Значит,
P(A) = 1-
P( A )
![]()
=1 – 0,006 = 0,994.
Ответ: 0,994.
13-й Порок мира взрослых – Азартные игры в теории вероятностей.
Большой, интересный и не очень известный памятник находится в самом центре Москвы, в сквере на Болотной площади. Он называется «Дети – жертвы пороков взрослых». Хотя памятником, в классическом понимании этого слова, наверное, его назвать нельзя. Эта целая скульптурная композиция, целая история, которую не расскажешь в двух словах.

Он появился в столице 2 сентября 2001 года в День города. Его автор – Михаил Шемякин. По словам художника, когда он только задумал композицию, он хотел одного – чтобы люди задумались о спасении сегодняшнего и будущего поколений. Многие, кстати в то время были против его установки недалеко от Кремля. Даже собирали специальную комиссию в столичной Думе, и та также высказалась против. Но, действующий в то время мэр Юрий Лужков всё взвесил и дал добро.
Памятник действительно выглядит неоднозначно и непривычно. Он входит в топ-10 самых скандальных памятников Москвы. Композиция состоит из 15 фигур, две из которых маленькие дети – мальчик и девочка лет 10. Они расположены в самом центре. Как и все в этом возрасте, они играют в мячик, у них под ногами лежат книги сказок. Но у детей завязаны глаза, они не видят, что вокруг стоят 13 страшных высоченных фигур, тянущих к ним руки-щупальца. Каждое изваяние олицетворяет какой-то порок, который может развратить детские души и навсегда ими завладеть.

Стоит подробно описать каждую (слева направо):
Наркомания. Худощавый мужчина во фраке и бабочке, чем-то напоминает графа Дракулу. В одной руке шприц, а в другой – пакетик с героином.
Проституция. Этот порок представлен в образе мерзкой жабы с выпученными глазами, нарочито вытянутым ртом и пышным бюстом. Всё её тело покрыто бородавками, а на поясе вьются змеи.
Воровство. Хитрая свинья, которая повернулась спиной, явно чего-то пряча. В одной руке у нее мешочек с деньгами.
Алкоголизм. Жирный слащавый полуголый человек, восседающий на бочке с вином. В одной руке у него кувшин с чем-то «горячим», в другой пивной кубок.
Невежество. Веселый и беззаботный осел с большой погремушкой в руках. Живая иллюстрация поговорки «меньше знаешь, лучше спишь». Правда, тут лучше сказать «нет знаний, нет проблем».
Лженаучность. Женщина (вероятно) в монашеской рясе с закрытыми глазами. В одной руке у неё свиток с псевдознаниями. Рядом стоит непонятный механический прибор, а в другой руке результат неправильного применения науки – двухголовая собака, которую держат как марионетку.
Равнодушие. «Не так страшны убийцы и предатели, они могут только убить и предать. Страшнее всего – равнодушные. С их молчаливого согласия происходит всё самое худшее в этом мире». Видимо, автор полностью согласен с этим изречением. Он поместил «Равнодушие» в самый центр пороков. Фигура имеет четыре руки – две скрещены на груди, а другие две затыкают уши.
Пропаганда насилия. Фигура напоминает Буратино. Только у него в руке щит, на котором изображено оружие, а рядом стопка книг, одна из которых «Майн Кампф».
Садизм. Толстокожий носорог отлично подходит для иллюстрации этого порока, к тому же одет он в наряд мясника.
Беспамятство. Позорный столб - единственная неодушевленная фигура в общей композиции.
Эксплуатация детского труда. То ли орел, то ли ворон. Человек-птица приглашает всех на заводик, где трудятся дети.
Нищета. Иссушенная босая старуха с посохом протягивает руку, прося милостыню.
Война. Последний персонаж в списке пороков. Человек, закованный в доспехи, и с противогазам на лице, протягивает детям игрушку – всеми любимого Микки-Мауса, но мышонок закован в бомбу
Но там нет еще одного страшного Порока мира Взрослых – «Приобщение к азартным играм»
Самый распространенный тип зависимости среди молодежи – это зависимость от игровых автоматов. Огромное количество подростков после занятий, а то и вместо них бегут к «одноруким бандитам» в надежде выиграть и быстро и легко получить деньги, при этом теряя их. Проигрывают, ищут возможности их найти, порой криминальные, чтобы опять скормить их груде металла.
Не редко встречаются ситуации, когда предлагают, прям на улице испытать удачу – билетики с выигрышными номерами на несколько человек. Или сыграть вот в такую игру: кидают 6 карандашей, на каждой грани – числа от 1 до 6. Почему карандаши? К кубикам якобы меньше доверия. Сумма выпавших чисел суммируется. Если выпадет от 6 до 15 очков или от 30 до 36 очков -0 большой выигрыш, а если от 15 до 30 очков – то проигрыш. Как утверждают организаторы игры – выигрыш 50 на 50.
Подумайте, стали бы вы играть в такую игру? А если наоборот поменять условия выигрыша и проигрыша? В первом случае математики откажутся играть, а во втором – охотно согласятся, так как сумма очков из середины ряда 6-36 выпадает чаще.
Другой пример:
Бросают на стол 2 кубика. Нужно, чтобы выпала сумма очков =5. Сколько вариантов? 1+4, 2+3, 3+2, 4+1, т.е. 4 варианта. А сколько всего вариантов выпадения на 2-х кубиках возможно? 6*6=36. Значит всего 36 способов.
Таким образом, подходит 4 способа из 36 возможных, поэтому вероятность того, что выпадет значение в 5 очков р=4/36=1/9=0,11111111.
Азартные игры появились практически на заре человечества. Сначала это были игральные кости, сводившие с ума еще древних египтян, затем появились карты, рулетка, лотереи …
Греху «зеленого сукна», красно-черной рулетки подвержены все люди – и мужчины, и женщины, независимо от возраста и социального положения. Все они, так или иначе, редко избегают соблазна повысить уровень адреналина в крови. В результате игр проматываются целые состояния, совершаются убийства, нарушаются законы: человеческие и божеские.
Кого-то может заинтересовать вопрос, способна ли теория вероятностей помочь в игре в залах игровых автоматов? Так вот: в течении дня администрация любого зала имеет возможность ни один раз перепрограммировать автоматы в зависимости от того, как складывается день, чтобы быть в выигрыше. Так что теория вероятностей в данном случае не поможет.
«Болезнь игровая», «Игровая зависимость» - такие диагнозы, к сожалению, в последнее время не редкость.
Азартные игры – как наркотическая или алкогольная зависимости: вылечиться от этого нельзя, можно только бросить и никогда больше не притрагиваться. Наркомана или алкоголика можно поместить в клинику, а вот клиник, лечащих от игровой зависимости нет.
Домашнее задание.
Записываем домашнее задание: Выучить определения теории вероятностей. Самостоятельно придумать условия задачи и представить их решения.
5.Итоги урока.
Сегодня на уроке мы изучили понятия достоверных, невозможных, равновероятностных, противоположных, совместных и несовместных событий. Научились определять достоверность, возможность и невозможность событий. Изучили классическое определение вероятности и алгоритм решения задач по теории вероятности. Кто может повторить классическое определение вероятности? Что нового узнали на уроке? Понравились ли подобранные задачи? Чем? Прошу вас оценить свою работу на уроке? Что понравилось на уроке, а что нет? Учащиеся высказывают своё мнение, подводят общий итог урока. Преподаватель отмечает, в какой мере достигнуты цели, выполнены задачи урока; говорит о дальнейшем плане изучения темы. Выставляются оценки за урок.
Дополнительные задачи:
1.Фабрика выпускает сумки. В среднем на 180 сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решение
N(A) = 180-8 = 172 сумки качественные;
N= 180 всего сумок.
| P ( A) | 172 | 0, 955... 0, 96 |
|
| 180 |
| ||
|
|
|
|
Ответ: 0,96.
2.В случайном эксперименте симметричную монету бросают трижды.
Найдите вероятность того, что орел выпадет ровно два раза.
Решение
Всего вариантов N = 2×2×2=8.
Благоприятных N(A) = 3 варианта: о; о; р , о; р; о , р; о; о .
Вероятность равна
Ответ: 0,375.
| P ( A) | 3 | 0, 375 |
|
| 8 |
| ||
|
|
|
|
Литература.
Основные источники:
1. Богомолов, Н.В. Математика. Учебник для СПО. Рекомендовано Учебно-методическим отделом СПО в качестве учебника для СПО [Текст] / Н.В. Богомолов - М.: Юрайт, 2015
2. Богомолов, Н.В. Практические занятия по математике. Учебное пособие для СПО. Рекомендовано Учебно-методическим отделом СПО [Текст] / Н.В. Богомолов - М.: Юрайт, 2016
3. Богомолов, Н.В. Математика. Задачи с решениями. Том 1. Учебное пособие для СПО. Рекомендовано Учебно – методическим отделом СПО в качестве учебного пособия для СПО [Текст] / Н.В. Богомолов – М.: Юрайт, 2015
4. Богомолов, Н.В. Математика. Задачи с решениям. Том 2. Учебное пособие для СПО. Рекомендовано Учебно – методическим отделом СПО в качестве учебного пособия для СПО [Текст] / Н.В. Богомолов – М.: Юрайт, 2015
Дополнительные источники:
5. Омельченко, В.П. Математика. Допущено Министерством образования РФ в качестве учебного пособия для СПО [Текст] / В.П. Омельченко - Ростов н/Д.: Феникс, 2012
6. Богомолов, Н.В. Сборник дидактических заданий по математике [Текст] / Н.В, Богомолов - М.: Дрофа, 2009
Раздаточный материал:
Ф.И.О._______________________________________________________
Для каждого из перечисленных событий определите, какое оно:
достоверное, возможное, невозможное:
Солнце кружится вокруг Земли;
Ваше участие в летних олимпийских играх;
Вы выиграли в викторине;
В 9-м классе школьники не изучают геометрию;
Мама старше своих детей;
Вам за урок поставят оценку «4»;
Параллельные прямые не пересекаются.
| Событие | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Достоверное |
|
|
|
|
|
|
|
|
| Возможное |
|
|
|
|
|
|
|
|
| Невозможное |
|
|
|
|
|
|
|
|
Поменяйтесь с соседом по парте заданиям. И давайте проверим верность выполненного задания. После проверки оцените работу.
Задача 2. Из 20 учащихся класса двое справляют день рождения: 1). 30 января; 2). 30 февраля. Определите, каким является каждое из событий: невозможным, достоверным, или случайным.
Решение:1). Событие, заключающееся в том, что двое из 20 учащихся родились 30 января – случайное, оно может произойти, а может и не произойти (все зависит от состава группы из 20 учеников).
2). Второе событие – невозможное, поскольку даты 30 февраля не существует, следовательно, никто из учащихся не мог родиться в такой день.
Ответ: 1). Случайное, 2). Невозможное.
Задача 3. Из событий:
1). «идет дождь»;
2). «на небе нет ни облачка»;
3). «наступило лето»
– составить среди них пары совместимых и пары несовместимых.
Р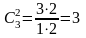 ешение. Из трех событий можно образовать 3 различных пары (порядок событий в паре значения не имеет); количества пар равно
ешение. Из трех событий можно образовать 3 различных пары (порядок событий в паре значения не имеет); количества пар равно
Это: 1). – 2). ; 1). – 3). ; 2). – 3).
События в 1 паре несовместные, во 2 паре – совместные, в 3 – совместные.
Ответ: 1 пара несовместных и 2 пары совместных событий.
Задача 4. Охарактеризуйте событие, о котором идет речь, как достоверное, невозможное или случайное. Вы открыли эту книгу на любой странице и прочитали первое попавшееся существительное. Оказалось, что:
В написании выбранного слова есть гласная буква
В написании выбранного слова есть буква «О»
В написании выбранного слова нет гласных букв
В написании выбранного слова есть мягкий знак.
Решение:
а). Событие достоверное, т.к. в русском языке нет существительных состоящих только из согласных букв.
b). Событие случайное.
c). Событие невозможное (см. а)
d). Событие случайное.
Ответ: a). Достоверное, b). Случайное, с). Невозможное, d). Случайное.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Урок по математике на тему: "Теория вероятностей" (2.4 MB)
Урок по математике на тему: "Теория вероятностей" (2.4 MB)
 0
0 360
360 4
4 Нравится
0
Нравится
0


