Республика Казахстан г. Актобе ОСШ № 25
ТЕМА: МЕТОДЫ ИСПОЛЬЗОВАНИЯ ОГРАНИЧЕННОСТИ ФУНКЦИЙ
Жизнь хороша тем, что в ней
можно заниматься математикой
/Леонард Эйлер/
Цели:
Образовательная: обучить учащихся порядку и правилам решения задач по математике, практическому применению возможностей приложения Microsoft Office Excel.
Развивающая: развивать у учащихся познавательный интерес к учебным дисциплинам, умение применять свои знания на практике.
Воспитательная: воспитывать внимание, аккуратность, расширять кругозор учеников.
Для того чтобы узнать тему сегодняшнего урока нужно выполнить следующие задания, расставив ответы в порядке убывания.
| ограниченности | метод | использования | функций |
| 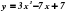 Найти абсциссу точки графика функции Найти абсциссу точки графика функции
, в которой тангенс угла касательной равен -1. | 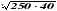 Найти значение выражения Найти значение выражения
| 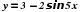 Укажите наибольшее значение функции Укажите наибольшее значение функции
| 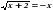 Решите уравнение Решите уравнение
|
| Ответ: 1 | Ответ: 10 | Ответ: 5 | Ответ: -1 |
ОТВЕТ: 10; 5; 1; -1 (Метод использования ограниченности функций).
Рассмотрим теорию:
Одним из эффективных методов решения уравнений или неравенств является метод, основанный на использовании ограниченности функций. К наиболее известным ограниченным функциям относятся, например, некоторые тригонометрические; обратные тригонометрические функции; функции, содержащий модуль, степень, корень с чётной степенью и другие.
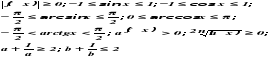 Наиболее распространёнными неравенствами являются следующие:
Наиболее распространёнными неравенствами являются следующие:
и многое другое.
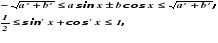 Кроме приведенных простейших неравенств имеются и более сложные, в частности, тригонометрические неравенства
Кроме приведенных простейших неравенств имеются и более сложные, в частности, тригонометрические неравенства
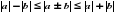 и неравенства с модулями вида
и неравенства с модулями вида
Обширные возможности в исследовании функций на их ограниченность нам предоставляет функционал Microsoft Office Excel. Так функционал построения диаграмм позволяет организовать построение графиков функций и их наглядность при изучении ограниченности функций.
Подготовленный пример файла Excel позволяет продемонстрировать функциональность приложения. Для наглядности решим пример 1.
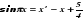 Пример 1:
Пример 1:
Решить уравнение:
Для решения уравнения определяем ограниченность представленных функций. Из значений тригонометрических функций нам известно, что результатом функции SIN() является диапазон чисел от -1 до 1, т.е. функция SIN (Pi*x) при различных вариантах изменения х на выходе будет иметь своим максимумом 1 и минимумом -1. Квадратичная функция в правой стороне уравнения обладает графиком функции в виде параболы с минимальной точкой и симметричными ветвями. Приравняем каждую часть уравнения к max первой функции 1, если решение для второго уравнения при его приравнивании к 1 не будет найдено, то это будет свидетельствовать об отсутствии решения (графики данных функций не пересекаются), все решения будут свидетельствовать о количестве точек пересечения графиков функций.
Получаем следующую систему уравнений:
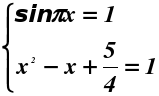
Решаем первое уравнение: SIN (Pi*x) = 1
SIN (Pi*x) = SIN (Pi/2)
Pi*x = Pi/2
x = Pi/(2*Pi) = ½
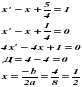 решаем второе уравнение, получаем
решаем второе уравнение, получаем
Найденное решение уравнения свидетельствует о наличии точки пересечения графиков функций (x = 1/2, y = 1). Для наглядности введем функции в подготовленное приложение Excel и рассмотрим графики на отрезке от -1 до 1. Как мы можем увидеть графики функций действительно пересекаются в одной единственной точке (1/2, 1).
ОТВЕТ: 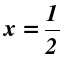
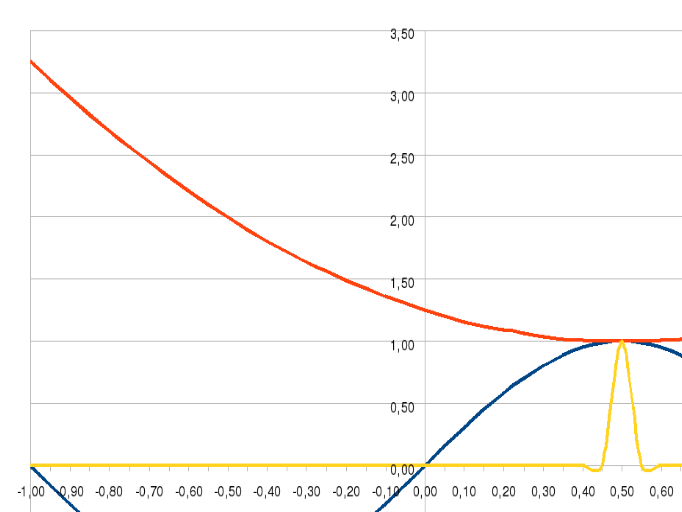
Рассмотрим второй пример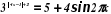 :
:
Ограниченность функций данного уравнения заключается в ограниченности возможных входных данных: так первая функция (левая) ограничена по степени в которую будет возводиться основание (3). |4x-1|+2 никогда не будет меньше 2, т.к. минимальным значением |4x-1| может быть только 0 и не менее. Минимальным значением левой функции в таком случае является 32 = 9. Правая функция ограничена значением тригонометрической функции SIN(), её значение как мы помним из решения первого уравнения находиться в пределах от -1 до 1, таким образом вторая функция имеет минимальное своё значение при минимальном синусе и максимальное значение при его максимуме. Таким образом минимум функции находится в точке 5+4*(-1) = 1, а максимум в точке 5+4*1 = 9. Заметно, что минимум первой функции совпадает с максимумом второй функции. Опишем следующую систему уравнений:
Получаем, что первое уравнение равно 9 при х = ¼.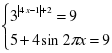
Максимального своего значения тригонометрическая функция синуса достигает при SIN(Pi/2), т.е
2*Pi*x = Pi/2
x = Pi/(2*2*Pi) = ¼
Как видим решение данной системы уравнения находится в точке (х = 1/4, y = 9). Проверим наше решение в приложении Excel.
Как мы видим наше решение находит своё отражение и на графиках функций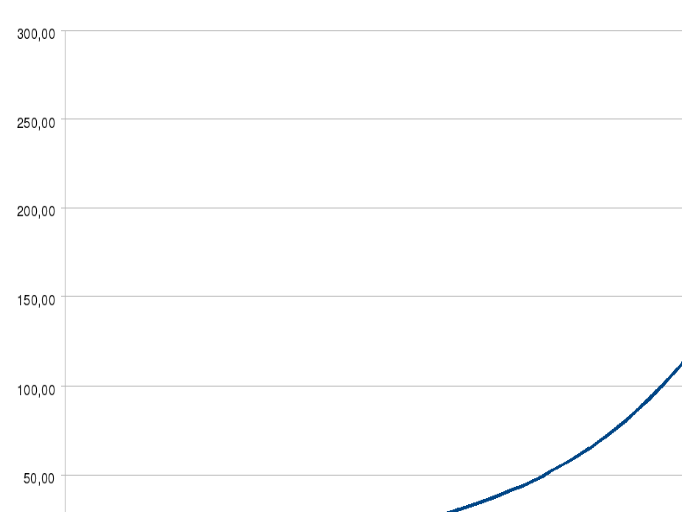
ОТВЕТ: 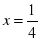
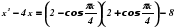
Приступим к решению следующего уравнения № 3
Первая функция как можно догадаться принимает любые значения х, т.к. в ней отсутствуют какие-либо ограничения. Как мы знаем степенные функции имеют график в виде параболы и вне зависимости от подставляемого в неё отрицательного числа на выходе будем иметь положительный результат, т.к. возводя отрицательное число в квадрат мы получаем положительное число. Т.к. график степенной функции симметричен, точку минимума мы найдём через точки пересечения графика с осью абсцисс. Сделаем мы это приравняв функцию к нулю. x2 – 4x = 0
x*(x - 4) = 0
Таким образом мы находим что график первой функции пересекает ось абсцисс в двух точках при х = 0 и х = 4. Отсюда следует, что точка минимума (середина отрезка) находиться в точке при х = (4-0)/2 = 2, т.е. 22 – 4*2 = -4. Точка минимума для первой функции (2, -4).
Вторая функция (правая сторона нашего уравнения) ограничена результатами тригонометрической функции COS(), который может быть от -1 до 1. Расчитаем минумум и максимум второй функции при y = -1, cos (Pi*x/4) = -1 = cos (Pi)
(Pi*x)/4 = Pi
при х = 4
y = 1, cos (Pi*x/4) = 1 = cos (0) или cos(2*Pi)
(Pi*x)/4 = 0 (Pi*x)/4 = 2*Pi
при х = 0 или x = 8
Как мы видим из формулы максимальное и минимальное значение COS() приводят к минимальному значению всей функции, т.к. множители просто меняются местами:
(2 – COS((Pi*4)/4))*(2 + COS((Pi*4)/4))-8 = (2 + 1)*(2 - 1) - 8 = -5
(2 – COS((Pi*0)/4))*(2 + COS((Pi*0)/4))-8 = (2 - 1)*(2 + 1) - 8 = -5
(2 – COS((Pi*8)/4))*(2 + COS((Pi*8)/4))-8 = (2 - 1)*(2 + 1) - 8 = -5
Ограничим влияние тригонометрической функции на функцию в целом приравняв её к нулю
(2 – 0)*(2 + 0)-8 = (2*2) - 8 = -4 получаем точку максимума для второй функции. Точка минимума для первой функции нам известна – это (2, -4) проверим систему уравнений при приравнивании функций к -4
х2-4х = -4
(2 – COS((Pi*x)/4))*(2 + COS((Pi*x)/4))-8 = -4
(2 – COS((Pi*x)/4))*(2 + COS((Pi*x)/4)) = 4
4 + 2 COS((Pi*x)/4) - 2 COS((Pi*x)/4) – COS2((Pi*x)/4) = 4
4 - COS2(Pi*x)/4) = 4
COS2((Pi*x)/4) = 0
COS((Pi*x)/4) = 0
COS((Pi*x)/4) = COS(Pi/2)
(Pi*x)/4 = Pi/2
x = 4Pi/2Pi = 2
Таким образом мы приходим к выводу что графики функций пересекаются с точке (2, -4)
В Excel это будет выглядеть следующим образом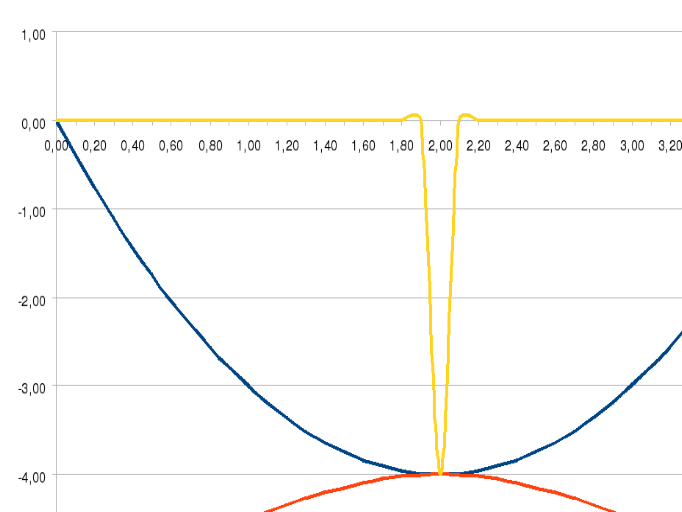
Ответ: 2
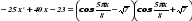 В четвёртом примере мы рассмотрим следующее уравнение
В четвёртом примере мы рассмотрим следующее уравнение
Начнём решение данного уравнения с анализа правой стороны нашего уравнения. Исходя из ограниченности выходных данных тригонометрических функций рассмотрим два крайних результата выдаваемых функцией при сos(5PiX/8) = 1 и -1, а также при равенстве 0.
В первом варианте y = (1 – 71/2)(1+71/2) = 1 – 7 = -6 (max)
y = (-1 – 71/2)(-1+71/2) = 1 – 7 = -6 (max)
y = (0 – 71/2)(0+71/2) = -7 (min)
Как видим вторая функция ограничена в пределах от -7 до -6.
Создаём систему уравнений
-25х2+40х-23=-7
(cos(5Pix/8) – 71/2)( cos(5Pix/8)+71/2)=-7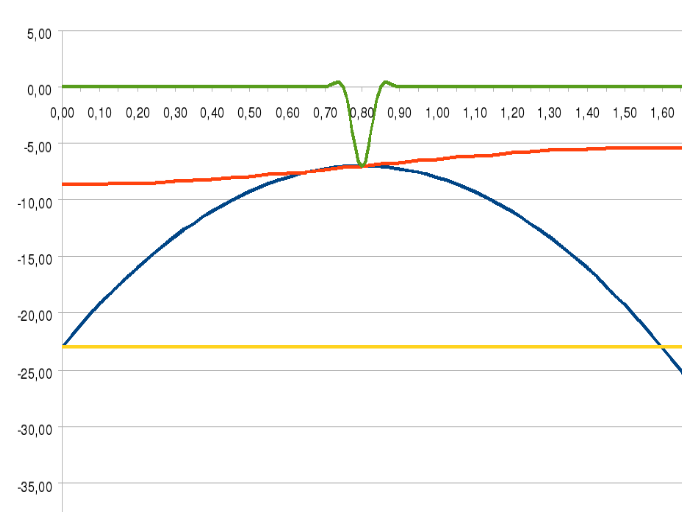
Находим корни для первого уравнения:
х = 0,8
cos(5Pix/8) = 0
cos(5Pix/8) = cos(Pi/2)
5Pix/8 = Pi/2
х = 8Pi/10Pi = 8/10 = 0,8
Ответ: 0,8
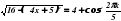
ПРИМЕР 6: Решить уравнение:
Функция левой стороны уравнения ограничена отсутствием возможности извлечения квадратного корня из отрицательного числа
16 – (4х +5)2 = 0
Таким образом мы видим, что функция существует только на отрезке от на котором выполняется условие
(4х +5)2 4х +5 = -4
4x x = -9
x max) x = -9/4 = -2,25 (min)
График функции симметричен и мы можем найти точку максимума -0,25 – (-2,25) = 2
Отрезок существования функции 2 единицы, т.о. точка максимума графика функции в точке (max) = -2,25 + (2/2) = -2,25 + 1 = -1,25
В этой точке левая функция имеет f(x) = 4
Правая функция ограничена выходными данными тригонометрической функции COS()
т.к. в функции находиться квадрат COS() его результат заведомо является положительным числом. Ограниченность правой функции по оси ординат составляет от 4 до 5. Как мы видим обе функции могут пересекаться только в точке 4 по оси ординат.
Система уравнений выглядит следующим образом
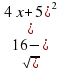
4 + COS(2Pix/5) = 4
только при COS(2Pix/5) = 0
COS(2Pix/5) = COS(Pi/2) для 90 градусов
2Pix/5 = Pi/2
x = 5Pi/4Pi
x = 1,25
Принимая во внимание тот факт что правая функция является периодичной необходимо найти её шаг
COS(2Pix/5) = COS(3Pi/2) для 270 градусов
2Pix/5 = 3Pi/2
x = 15Pi/4Pi
x = 3,75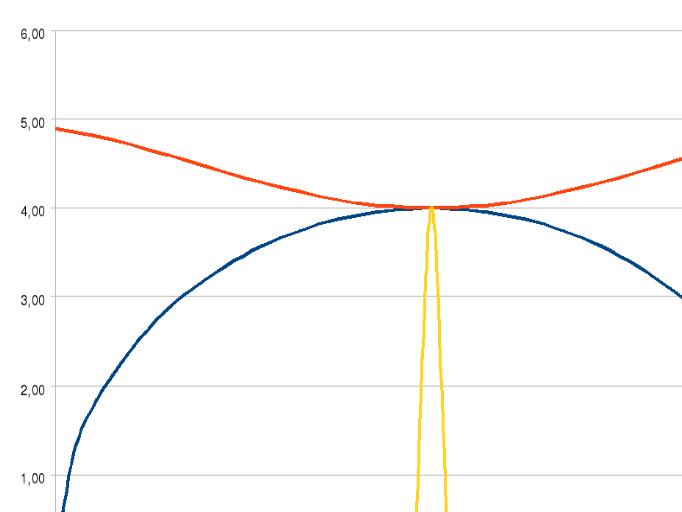
Составляем пропорцию 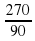 =
= 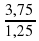 т.о. шаг на каждые 90 градусов составляет 1,25. Отсюда следует что точка (-1,25, 4) принадлежит обеим функциям и является решением уравнения.
т.о. шаг на каждые 90 градусов составляет 1,25. Отсюда следует что точка (-1,25, 4) принадлежит обеим функциям и является решением уравнения.
ОТВЕТ: -1,25


 Получите свидетельство
Получите свидетельство Вход
Вход



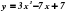 Найти абсциссу точки графика функции
Найти абсциссу точки графика функции 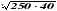 Найти значение выражения
Найти значение выражения 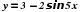 Укажите наибольшее значение функции
Укажите наибольшее значение функции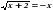 Решите уравнение
Решите уравнение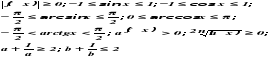 Наиболее распространёнными неравенствами являются следующие:
Наиболее распространёнными неравенствами являются следующие: 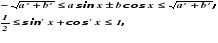 Кроме приведенных простейших неравенств имеются и более сложные, в частности, тригонометрические неравенства
Кроме приведенных простейших неравенств имеются и более сложные, в частности, тригонометрические неравенства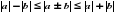 и неравенства с модулями вида
и неравенства с модулями вида 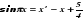 Пример 1:
Пример 1: 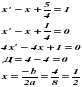 решаем второе уравнение, получаем
решаем второе уравнение, получаем
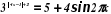 :
: 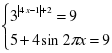

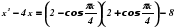

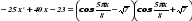 В четвёртом примере мы рассмотрим следующее уравнение
В четвёртом примере мы рассмотрим следующее уравнение
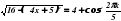
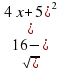

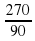 =
= 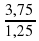 т.о. шаг на каждые 90 градусов составляет 1,25. Отсюда следует что точка (-1,25, 4) принадлежит обеим функциям и является решением уравнения.
т.о. шаг на каждые 90 градусов составляет 1,25. Отсюда следует что точка (-1,25, 4) принадлежит обеим функциям и является решением уравнения. 








 Урок по математике "Методы использования ограниченности функции" (91.94 КB)
Урок по математике "Методы использования ограниченности функции" (91.94 КB)
 0
0 475
475 83
83 Нравится
0
Нравится
0


