Тема урока: Трехгранный и многогранный угол
Цели урока:
ввести понятие трехгранного угла и его линейного угла;
рассмотреть задачи на применение этих понятий;
сформировать конструктивный навык нахождения угла между плоскостями;
рассмотреть задачи на применение этих понятий.
Ход урока
I. Организационный момент.
Сообщить тему урока, сформировать цели урока.
II. Актуализация знаний учащихся
1. Подготовка к изучению нового материала.
- Что называется углом на плоскости?
- Что называется углом между прямыми в пространстве?
- Что называется углом между прямой и плоскостью?
- Сформулируйте теорему о трех перпендикулярах
III. Изучение нового материала.
Понятие двугранного угла.
Фигура, образованная двумя полуплоскостями ![]() , проходящими через прямую МN, называется двугранным
, проходящими через прямую МN, называется двугранным
Полуплоскости - грани, прямая МN – ребро двугранного угла.
- Какие предметы в обыденной жизни имеют форму двугранного угла?
Угол между плоскостями АСН и СНD – это двугранный угол АСНD, где СН – ребро. Точки А и D лежат на гранях этого угла. Угол AFD – линейный угол двугранного угла АCHD
Алгоритм построения линейного угла
1 способ. На ребре взять любую точку О и провести перпендикуляры в эту точку (РО ![]() DE, KO
DE, KO ![]() DE) получили угол РОК - линейный.
DE) получили угол РОК - линейный.
2 способ. В одной полуплоскости взять точку К и опустить из нее два перпендикуляра на другую полуплоскость и ребро (КО и КР), тогда по теореме обратной ТТП РО![]() DE
DE
Все линейные углы двугранного угла равны Доказательство: лучи ОА и О1А1 сонаправлены, лучи ОВ и О1В1 тоже сонаправлены, углы ВОА и В1О1А1 равны как углы с сонаправлеными сторонами.
Градусной мерой двугранного угла называется градусная мера его линейного угла
IV. Закрепление изученного материала.
Решение задач
1. РАВС – пирамида; угол АСВ равен 90о, прямая РВ перпендикулярна плоскости АВС. Доказать, что угол РСВ – линейный угол двугранного угла с
2. РАВС - пирамида; АВ = ВС, D – середина отрезка АС, прямая РВ перпендикулярна плоскости АВС. Доказать, что угол PDB – линейный угол двугранного угла с ребром АС.
3. PABCD – пирамида; прямая РВ перпендикулярна плоскости АВС, ВК перпендикулярна DC. Доказать, что угол РКВ – линейный угол двугранного угла с ребром СD.
Задачи на построение линейного угла
1. Построить линейный угол двугранного угла с ребром АС, если в пирамиде РАВС грань АВС – правильный треугольник, О – точка пересечения медиан, прямая РО перпендикулярна плоскости АВС
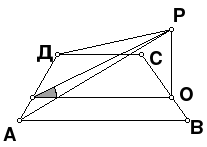
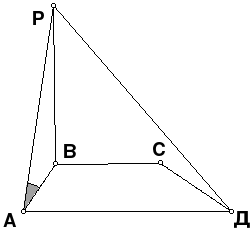
2. Дан ромб АВСD.Прямая РС перпендикулярна плоскости АВСD.
Построить линейный угол двугранного угла с ребром ВD и линейный угол двугранного угла с ребром АD.
Вычислительная задача.
В параллелограмме АВСD угол АDС равен 1200, АD = 8 см,
DС= 6 см, прямая РС перпендикулярна плоскости АВС, РС= 9 см.
Найти величину двугранного угла с ребром АD и площадь параллелограмма.
| № | Вариант 1.
| Вариант 2. |
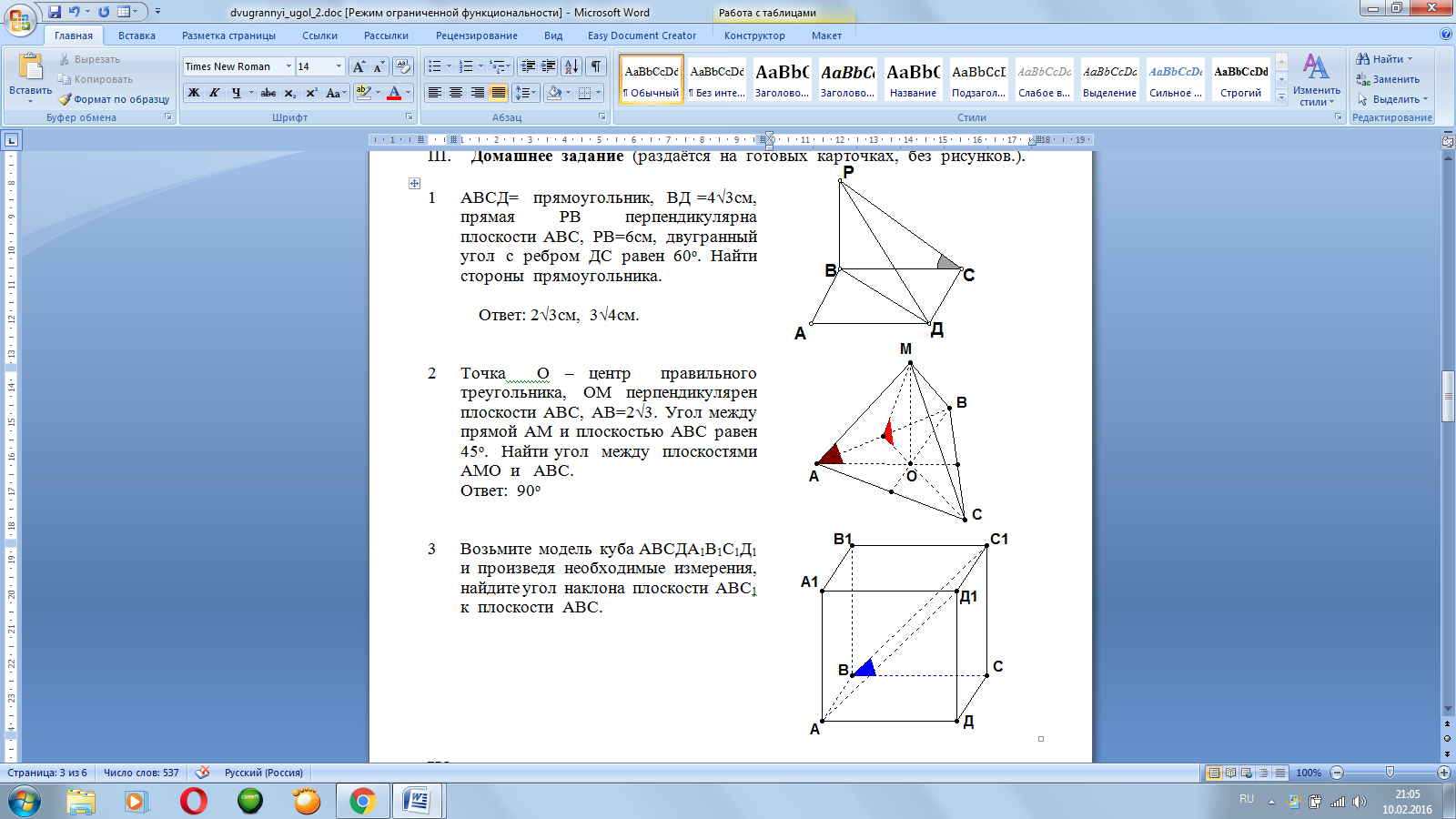
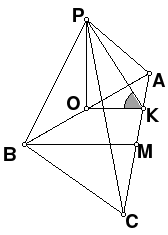
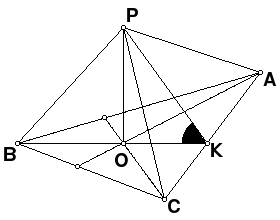
| 1. | Дан прямоугольник АВСД и точка Р вне его плоскости. Построить линейный угол двугранного угла с ребром ДС, если прямая ВР перпендикулярна плоскости АВС.
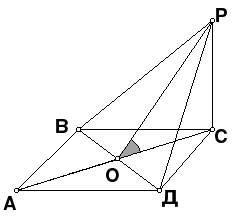
| Дан ромб АВСД; прямая РС перпендикулярна плоскости АВС. Построить линейный угол двугранного угла с ребром ВД..
|
| 2. | Построить линейный угол двугранного угла с ребром АД, если АВСД – трапеция, угол ВАД равен 90о, прямая РВ перпендикулярна плоскости АВС.
| Построить линейный угол двугранного угла с ребром АД, если АВСД – трапеция, угол ВАД равен 90о, точка О принадлежит отрезку ВС, прямая РО перпендикулярна плоскости АВС. |
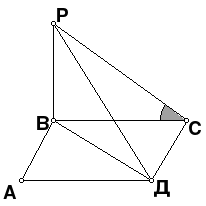
| 3. | Дана пирамида РАВС. Найти величину двугранного угла с ребром АС, если Грань АВС – правильный треугольник, АВ=6см, О – точка пересечения медиан, прямая ОР перпендикулярна плоскости АВС, ОР=4см.
Ответ: α=arctg 2,4 | Дана пирамида РАВС. Найти величину двугранного угла с ребром АС, если Грань АВС – правильный треугольник, точка О – середина отрезка АВ, АВ=6см, прямая ОР перпендикулярна плоскости АВС, ОР=4см.
Ответ: α=arctg 1,5396
|
V. Домашнее задание

 Получите свидетельство
Получите свидетельство Вход
Вход












 Урок на тему; "Трехгранный и многогранный угол" (235.18 KB)
Урок на тему; "Трехгранный и многогранный угол" (235.18 KB)
 0
0 1152
1152 152
152 Нравится
0
Нравится
0


