Урок математики "Сложение рациональных чисел"

 - Сформировать способность к сложению рациональных чисел, использованию свойств сложения для реализации вычислений.

 - Повторить и закрепить: свойства сложения, сравнение рациональных чисел, решение уравнений, содержащих знак модуля, совместные действия с обыкновенными и десятичными дробями.

 - развивать воображение, мышление, творческий потенциал

 - воспитывать настойчивость, терпение, самостоятельность.

ХОД УРОКА.

 Девизом нашего урока будут слова В. А. Сухомлинского: “Презирай лень мысли”.

 - Как вы понимаете эти слова?

 - Какое у вас сейчас настроение?

I Актуализация знаний.

Устный блок

а). Соединить стрелками в порядке возрастания числа.

 в). Подобрать два отрицательных числа, чтобы выполнялись 2 соотношения

г)Задача. На олимпиаде по математике верное решение первой задачи оценивалось в 5 очков, а верное решение второй задачи в 3 очка; неверное решение первой задачи оценивалось в - 5 очков, а неверное решение второй задачи в - 3 очка. Ответьте на вопросы:

1. Сколько баллов заработал Петя, если он верно решил обе задачи?

2. А как подсчитать количество очков, если обе задачи решены неверно?

  - 5 + ( - 3)

3. Он неверно решил первую задачу и верно вторую

 - 5 + 3

4. Верно первую, и неверно вторую 5 + ( - 3)

д) Ромашка

II Актуализация знаний.

 - Вспомнить различные ситуации из жизни, когда нам приходится иметь дело со сложением положительных и отрицательных чисел.

Температура воздуха

Получение и трата денег

Таблица результатов игр футбольных матчей.

 - Что такое координатная прямая?

 - Какие числа называются противоположными?

 - Как сложить числа с одинаковыми знаками?( Чтобы сложить числа с одинаковыми знаками надо сложить их модули и перед результатом поставить их общий знак)

 - Как сложить числа с разными знаками? ( Надо из большего модуля вычесть меньший модуль и поставить знак того слагаемого, модуль которого больше)

  - Чему равна сумма противоположных чисел? (Нулю)

 - Как сравнивают рациональные числа? (Всякое положительное число больше нуля и больше любого отрицательного, всякое отрицательное число меньше нуля и меньше всякого положительного, из двух отрицательных чисел больше то, модуль которого меньше).

 - Как раскрыть скобки, перед которыми стоит знак + или - ?

ИСТОРИЧЕСКАЯ СПРАВКА

 Отрицательные числа появились значительно позже натуральных чисел и обыкновенных дробей. Первые сведения об отрицательных числах встречаются у китайских математиков во II в. до н. э. Положительные числа тогда толковались как имущество, а отрицательные – как долг, недостача.

 Но ни египтяне, ни вавилоняне, ни древние греки отрицательных чисел не знали. Лишь в VII в индийские математики начали широко использовать отрицательные числа, но относились к ним с некоторым недоверием. Складывать и вычитать отрицательные числа научились древнекитайские ученые еще до нашей эры.

 Индийские математики представляли себе положительные числа как “имущество”, отрицательные числа – как “долги”. Вот как индийские математик Брахмагупта излагал правила сложения и вычитания: “Сумма двух имуществ есть имущество”, “Сумма двух долгов есть долг”, “Сумма имущества и долга равна их разности”.

 В Европе отрицательными числами начали пользоваться с XII - XIII вв, но до Х/I в. как и в древности , они понимались как долги, большинство ученых считали их “ложными” в отличие от положительных чисел - “истинных”.

 Признанию отрицательных чисел способствовали работы французского математика, физика и философа…. . Он предложил геометрическое истолкование положительных и отрицательных чисел - ввел координатную прямую (1637). Его фамилию мы расшифруем!!! Рене Декарт(1596 - 1650).

Весь материал – смотрите документ.

5

ТЕМА: СЛОЖЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ

Цель:

-Сформировать способность к сложению рациональных чисел, использованию свойств сложения для реализации вычислений.

-Повторить и закрепить: свойства сложения, сравнение рациональных чисел, решение уравнений, содержащих знак модуля, совместные действия с обыкновенными и десятичными дробями.

-развивать воображение, мышление, творческий потенциал

-воспитывать настойчивость, терпение, самостоятельность.

ХОД УРОКА.

Девизом нашего урока будут слова В.А.Сухомлинского: “Презирай лень мысли”.

- Как вы понимаете эти слова?

- Какое у вас сейчас настроение?

I Актуализация знаний.

Устный блок

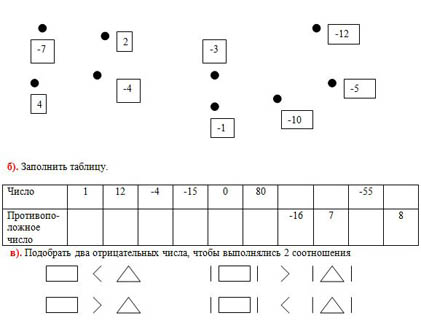
а). Соединить стрелками в порядке возрастания числа.

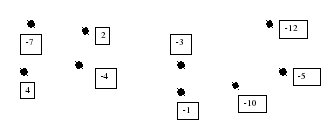
б). Заполнить таблицу.

в). Подобрать два отрицательных числа, чтобы выполнялись 2 соотношения

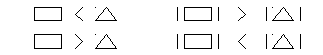
г)Задача. На олимпиаде по математике верное решение первой задачи оценивалось в 5 очков, а верное решение второй задачи в 3 очка; неверное решение первой задачи оценивалось в -5 очков, а неверное решение второй задачи в -3 очка. Ответьте на вопросы:

1.Сколько баллов заработал Петя, если он верно решил обе задачи?

2. А как подсчитать количество очков, если обе задачи решены неверно?

-5 + (-3)

3. Он неверно решил первую задачу и верно вторую

-5 + 3

4. Верно первую, и неверно вторую 5 + (-3)

д) Ромашка

II Актуализация знаний.

-Вспомнить различные ситуации из жизни, когда нам приходится иметь дело со сложением положительных и отрицательных чисел.

• Температура воздуха

• Получение и трата денег

• Таблица результатов игр футбольных матчей.

-Что такое координатная прямая?

-Какие числа называются противоположными?

-Как сложить числа с одинаковыми знаками?( Чтобы сложить числа с одинаковыми знаками надо сложить их модули и перед результатом поставить их общий знак)

-Как сложить числа с разными знаками? ( Надо из большего модуля вычесть меньший модуль и поставить знак того слагаемого, модуль которого больше)

-Чему равна сумма противоположных чисел? (Нулю)

-Как сравнивают рациональные числа? (Всякое положительное число больше нуля и больше любого отрицательного, всякое отрицательное число меньше нуля и меньше всякого положительного, из двух отрицательных чисел больше то, модуль которого меньше).

-Как раскрыть скобки, перед которыми стоит знак + или -?

ИСТОРИЧЕСКАЯ СПРАВКА

Отрицательные числа появились значительно позже натуральных чисел и обыкновенных дробей. Первые сведения об отрицательных числах встречаются у китайских математиков во II в. до н.э. Положительные числа тогда толковались как имущество, а отрицательные – как долг, недостача.

Но ни египтяне, ни вавилоняне, ни древние греки отрицательных чисел не знали. Лишь в VII в индийские математики начали широко использовать отрицательные числа, но относились к ним с некоторым недоверием. Складывать и вычитать отрицательные числа научились древнекитайские ученые еще до нашей эры.

Индийские математики представляли себе положительные числа как “имущество”, отрицательные числа – как “долги”. Вот как индийские математик Брахмагупта излагал правила сложения и вычитания: “Сумма двух имуществ есть имущество”, “Сумма двух долгов есть долг”, “Сумма имущества и долга равна их разности”.

В Европе отрицательными числами начали пользоваться с XII-XIII вв, но до Х\/I в. как и в древности , они понимались как долги, большинство ученых считали их “ложными” в отличие от положительных чисел - “истинных”.

Признанию отрицательных чисел способствовали работы французского математика, физика и философа…..Он предложил геометрическое истолкование положительных и отрицательных чисел - ввел координатную прямую (1637). Его фамилию мы расшифруем!!! Рене Декарт(1596-1650).

( ДЕКАРТ)

1) 26 +(-6) =

2) -70+56=

3) -17+30=

4) 80+ (-120)=

5) -6,3+7,8=

6) 0,39+(-0,39) =

Ответ: Д(20) ; Е(-14) ; К(13) ; А(-40) ; Р(1,5) ; Т(0) .

Окончательное и всеобщее признание как действительно существующие отрицательные числа получили лишь в первой половине ХVIII века. Тогда же утвердилось и современное обозначение для отрицательных чисел.

Действия над дробями еще в середине века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он “попал в дроби”. Чтобы облегчить действия с дробями, были придуманы десятичные дроби. В Европе их ввел в 1585 году голландский математик и инженер Симон Стевин.

III Отработка знаний.

Дата, Классная работа

1.Математический диктант с последующей проверкой.

(1 ученик работает за крыльями доски )

-2 + (-5) -1 + (-4) 4 + (-5,5)

-4 + 6 -1,5 + 3 -2 + (-8) + 2

3 + (-2) -5 + 2 -3,2 + 3,2

2. Найдите значение выражения:

а) -123,5 – (-2114,5) [Ответ. 1991].

б) (18,6 – (-958,4))·2 [Ответ. 1954].

12 февраля 1991 — по результатам всекрымского референдума Крымская область преобразована в Крымскую АССР в составе УССР

19 февраля 1954 — Крымская область передана из состава РСФСР в состав УССР. Передача была приурочена к празднованию 300-летия Переяславской Рады. Город Севастополь, как город республиканского подчинения, передан не был.

III Самостоятельная работа (на листочках)

1. Выполнить действия

-20 + (-5) 25 + (-15) -5 – (-6)

-5 + (-3) 20 – 35 16 – 26

-1,2 + (-0,3) 0 – 7 -23 – 25

-20 + 15 -7 – 5 -9 + 9

10 + 25 -6 – (-5) 14 – 24

2. Сколько решений имеет уравнение: | х - 8 | = -4

3. Угадай корни уравнения: 3,9 + х =0 -7 + у = -12 3 + а = -10

Физкультминутка.

«Минус с минусом сложить,
Можно минус получить.
Если сложишь минус, плюс,
То получится конфуз?!
Знак числа ты выбирай,
Что сильнее, не зевай!
Модули их отними
Да все числа помири!»

Задачи на сообразительность

1.Можно ли в решете принести воду?(лёд)

2.Как с помощью четырёх 5 получить 16? (55:5+5=16)

3. Что будет делать ворона, прожив 3 года? (житьчетвёртый)

5.Закрепление в тетради

Моя коллега учитель математики предложила шестиклассникам решить это задание дома. Как обычно, Витя Верхоглядкин сел за выполнение домашнего задания. Однако дело шло очень медленно. Тогда ему на помощь пришли мама, папа и бабушка. Они выполняли все действия по порядку, пока от усталости не стали смыкаться глаза. Наконец-то, сумма была найдена. На следующий день, во время завтрака, вся семья ругала неразумного учителя, задающего детям такие объемные задания. 

– А, вы, ребята, как бы решили задание, т.е. нашли значение следующего выражения:

– 499 + (– 498) + (– 497) + …+ 497 + 498+ 499 + 500?

Решение

Так как сумма противоположных чисел равна 0, то

– 499 + (– 498) + (– 497) + …+ 497 + 498+ 499 + 500 =

=500 + (– 499 + 499) + (– 498 + 498) + (– 497 + 497) + …+ (– 1 + 1) + 0 =

= 500 + 0 = 500.

Ответ: сумма всех целых чисел от – 499 до 500 равна 500.

Вспомогательные вопросы

1. Какими числами являются некоторые слагаемые?

2. Чему равна сумма противоположных чисел?

Какие свойства сложения можно применить?

6.Работа с учебником стр.204 № 1140(а-е)

Решить уравнение | х | = 8 2 | х | =6 | х - 8 | = -7

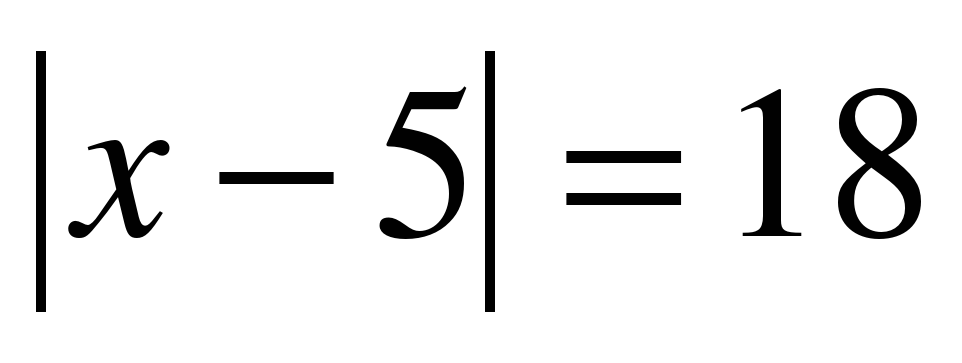
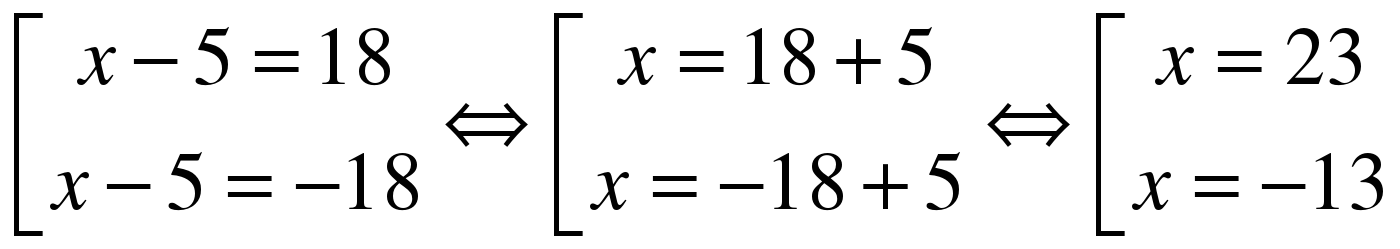
7.Рефлексия деятельности (итог урока)

• Что нового вы узнали на уроке?

• Оцените своё настроение на уроке.

• Полностью ли вы реализовали себя?

• Чем будем заниматься на следующем уроке? (Писать контрольную работу.)

8.Домашнее задание стр205 №8,9,10,11

Почему бьется оконное стекло

Спросил как- то наставник троих своих учеников:

"Почему бьется оконное стекло, когда в него бросают камень?"

-Потому, что камень тяжелый, отвечал один из них.

-Потому,что стекло хрупкое, изрек другой.

-Потому,что метнувшая камень рука была сильна и удар точный, ответил третий.

 -Никто из вас троих не дал правильного ответа, братья мои!

Потому что окно было закрыто!

Научитесь идти по Пути с открытыми сердцами, и ни одна вражеская стрела не разобьет их, проходя навылет сквозь тонкую ткань души.

Творческое задание.

- Человек обладает положительными и отрицательными качествами. Распределите эти качества на координатной прямой. К чему должен стремиться человек? Какими Качествами, которых у вас нет, вы бы хотели обладать?

Игорь идет к лесному озеру. Ему навстречу движется класс из 25 учеников и два преподавателя. Родители 10 детей также принимают участие в прогулке. Пять матерей еще везут своих детей на колясках. Преподаватель ведет с собой собаку. а двое детей ведут двух крыс.
Сколько ног идут по дороге к лесному озеру?