Цели урока:
• Формирование мыслительной культуры через логические рассуждения.
• Формирование навыка решения задач.
• Формирование умения сравнивать, применять полученные знания и навыки в нестандартных ситуациях.
Развивающие задачи:
• Развитие внимания учащихся, самостоятельности мышления.
• Применение учащимися смекалки, воображения и личного жизненного опыта.
Познавательные задачи:
• Развитие познавательного интереса к решению задач.
• Побуждение к поиску альтернативных решений.
• Развитие творческого подхода к решению математической задачи.
Оборудование: доска, карточки с задачами.
Ход урока
Устная разминка
Учитель: Как вы понимаете слова Владимира Маяковского "Книга - книгой, а мозгами двигай?" Помогает ли вам в жизни сообразительность, смекалка и такой "инструмент", как логическое мышление? Начнем урок с устной разминки.
1. Дана дробь:
В • А • Р • Е • Н • Ь • Е
К • А • Р • Л • С • О• Н
равная целому числу, разные буквы обозначают разные цифры, а между ними знак умножения. Чему равна дробь?
Ответ: Среди множителей должен быть ноль, т. к. десять букв обозначают десять цифр. Ноль может быть только в числителе дроби. Значит, она равна нулю.
2. Заметить закономерность ряда и записать по 2 числа.
2 , 4 , 6 , 8 , 10 , 12 , …
5 , 10 , 15 , 20 , 25 , 30 , …
2 , 3 , 5 , 7 , 11 , 13 , 17 , …
II. Решение задач
Учитель: Проверим, как полученные умения и навыки на уроках математики вам помогут при решении необычных задач. Решим вместе одну из задач.
Задача 1. Про множество А известно, что оно состоит из:
- различных натуральных чисел
- количество чисел больше 7
- НОК всех чисел из А равно 210
- НОД любых двух чисел больше 1
- произведение всех N из этого множества не равно квадрату целого числа.
- произведение этих чисел делится на 1920.
Найдите эти числа.
Решение: Разберем каждое условие.
1) Какие числа называются натуральными?
2) Их количество больше 7. Сколько их может быть?
3) Что такое НОК чисел? Как найти наименьшее общее кратное двух чисел? Давайте, разложим число 210 на простые множители.
210=3·7·2·5. Подберем всевозможные делители числа 210, перемножив сначала первый множитель на другие и т. д. В строчку будем выписывать получившиеся числа.
2 , 3 , 5 , 7 , 21 , 6 , 15 , 14 , 10 , 42 , 30 , 70 , 35 , 105 , 210.
3·7=21, 3·2=6, 7·2=14, 3·5=15, 7·5=35, 2·5=10, 3·7·2=42, 3·5·2=30, 7·5·2=70, 3·5·7=105
Если 210 делится на 105, то делится и на 2
4) НОД любых двух чисел больше 1. Значит эти числа взаимно - простые. Уберем числа 3, 2, 5, 7, 14, 35. Остались числа 6, 14, 10, 30, 42, 70, 105, 210
Проверим условие
5) произведение всех N из этого множества не равно квадрату целого числа. Как доказать, что нельзя получить квадрат целого числа? Представим множители в виде квадратов, используя свойство степени a2 · b2 =( a·b)2
2·3·7·2·2·5·7·3·2·3·7·5·2·5·7·3·3·7·2·5·2·5·3 = 27 · 36 · 55 · 75 = (23)2 · (33)2 · (52)2 · (72)2 · 2· 5· 7 = ( 23 · 33 · 52 · 72 )2
и еще останется 2 · 5 ·7 = 70. Следовательно, квадрат числа не получается.
Проверим последнее предложение. Произведение должно делиться на 1920. Определим, это не считая произведение и не выполняя деление в столбик. Запишем это предложение в виде дроби
Как упростить эту дробь?
Можно ли разложить на множители число 1920? 1920 = 5· 27 · 3
27 · 36 · 55 · 75
27 · 5 · 3
Дробь сокращается на 1920, тем самым выполняется и последнее условие.
Ответ: 6, 14, 10, 30, 42, 70, 105, 210.
Учитель: Какие понятия в этой задаче вам пришлось применять? Помогли вам в решении этой задачи приобретенные умения?
Ответ: НОД и НОК, простые, целые числа, разложение на множители. Запись произведения в виде произведение степеней, свойства степени.
III Самостоятельная работа в парах
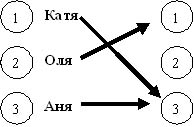
Задача 2 Аня, Катя и Оля были в одной комнате. Девочки видели, как одна из них разбила стакан. В ответ на вопрос, кто разбил стакан, Катя сообщила, что ни она, ни Оля ничего не разбивали. Оля сказала, что стакан разбила Катя, Аня призналась, что стакан разбила она. Кто разбил стакан, если одна девочка сказала правду, а две другие – нет?
Ответ: Стакан разбила Катя.
Решение:
1) Из Катиного ответа следует, что стакан разбила Аня, тогда Оля и Аня говорят, не правду - это соответствует условию.
2) Проверим другую версию. Пусть Аня сказала правду, тогда Катя нет и Оля нет. Значит, Катя говорит неправду и Оля, тогда и Оля и Катя разбили стакан, что противоречит условию задачи.
3) Пусть Оля сказала правду, тогда Катя покажет на Олю и Аня покажет на Олю, что противоречит условию.
Учитель: При решении логических задач можно использовать графы. Самостоятельно решите следующую задачу.
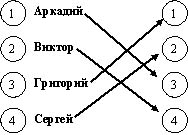
Задача 3 Аркадий, Виктор, Григорий и Сергей участвовали в шахматном турнире. На вопрос, какие места они заняли, были получены следующие ответы: Виктор не занял первого места, Сергей получил приз за второе место. Аркадий не занял ни первого места, ни последнего. Определите, какое место занял каждый?
Ответ:
Григорий - 1 место,
Сергей - 2 ,
Аркадий - 3,
Виктор - 4.
Учитель: Предлагаю принять участие еще в одном расследовании. А, вы знаете, что умение логически рассуждать необходимо не только математикам, но и следователям, юристам, управленцам.
Весь материал – смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход











 Урок математики "Решение логических задач" (39.63 КB)
Урок математики "Решение логических задач" (39.63 КB)
 0
0 848
848 63
63 Нравится
0
Нравится
0


