Цель урока: обобщение и систематизация знаний по теме: «Прямоугольная система координат»
Задачи:
Обучающие: обобщить и систематизировать знания; закрепить навыки решения задач по данной теме;
Развивающие: развивать коммуникативные качества личности через работу в парах; развитие познавательного интереса к предмету; развитие наблюдательности, самостоятельности, способности к коллективной работе.
Воспитывающие: воспитывать чувство ответственности взаимопомощи, аккуратности, трудолюбия.
Оборудование: интерактивная доска; карточки с заданиями на 8 вариантов для работы в парах; тесты в памяти компьютера; доска; маркеры.
Ход урока:
Вступительное слово учителя.
Математика - наука древняя, интересная и полезная. Сегодня мы с вами в очередной раз убедимся в этом, и очень хочется, чтобы каждый из вас для себя сделал хотя бы небольшое, но открытие. А как сказал великий ученый, математик Лейбниц: «Кто хочет ограничиться настоящим, без знания прошлого, тот его никогда не поймет». То и нам с вами для успешной работы нужно повторить решения задач методом координат. Задавая фигуры уравнения и выражая в координатах геометрические соотношение, мы применяем алгебру к геометрии. Так мы и поступили когда выразили через координаты основную геометрическую величину - расстояние между точками, а затем, когда вывели уравнения окружности и прямой. (Приложение)
Кроссворд « Рене Декарт»
1) Расстояние от точек окружности до центра (радиус)
2) Координатные оси разбивают плоскость на четыре части (четверти)
3) Точка равноудаленная от всех точек окружности (центр)
4) Точка, делящая отрезок на две равные части (середина)
5) Хорда, проходящая через центр окружности (диаметр)
6) Абсцисса с ординатой (координаты)
7) Число у точки М называют (ордината)
8) Через любые две точки можно провести (прямая)
9) Геометрическое место точек равноудаленных от данной точки (окружность)
10) Отрезок, соединяющий любые две точки окружности (хорда)
11) Число х точки М называют (абсцисса)
Историческая справка.
Я думаю, каждому из вас приходилось обращаться к прохожим с просьбой объяснить, где находится то или иное здание или учреждение.
А что делать мореплавателям? У кого им спросить дорогу в открытом море? Как объяснить другим, где находится открытый ими остров?
И вот 200 лет до нашей эры греческий Гиппарх предлагает вам известные географические координаты: широту и долготу. С помощью этих двух чисел можно точно определить положение острова, поселка, горы или колодца в пустыне и нанести их на карту или глобус. Научившись определять в открытом море широту и долготу местонахождения корабля, моряки получили возможность, никого не спрашивая, выбирать нужное им направление.
У одного из любимых всеми писателей, Жюля Верна, некоторые романы прямо построены на ситуациях, связанных с географическими координатами. В романе «Удивительные приключения дядюшки Антифера» одному из героев известна широта острова, на котором спрятаны сокровища, а другому - долгота этого острова. А вспомним текст записки из романа «Дети капитана Гранта»:
«7 июля 1862 года трехмачтовое судно «Британия» Глазго потерпело крушение. . . гони. . . южн. . . бере. . . два матроса. . . пл. Капитан Гр. . . дости. . . контин. . . пл. . . . жесток. . . инд. . . брошен этот документ. . . долготы и 37 11 широты. . . окажите им помощь. . . погибнут»
Сколько трудностей пришлось испытать героям романа, пока они нашли капитана Гранта, и все из - за того, что оказалось невозможным восстановить долготу.
В XIV в. французский математик Н. Оресм ввел по аналогии с географическими координаты на плоскости. Он предложил покрыть плоскость прямоугольной сеткой и называть широтой и долготой то, что мы теперь называем абсциссой и ординатой.
Это нововведение оказалось чрезвычайно продуктивным. На его основе возник метод координат, связавший геометрию с алгеброй. Основная заслуга в введении метода координат принадлежит французскому математику Р. Декарту(1596 - 1650). Такую систему координат стали называть декартовой.
На этой системе основаны многие способы указания места. Например, на билете в кинотеатр стоят два числа: ряд и место, - их можно рассматривать как координаты вашего места в зале. Подобные же координаты приняты в шахматах, правда, вместо одного из чисел берется буква: вертикальные ряды клеток обозначаются буквами латинского алфавита, а горизонтальные - цифрами.
Каждой клетке шахматной доски соответствует пара из буквы и числа, и, таким образом, шахматисты имеют возможность записывать свои партии.
Тот же «шахматный» принцип применяется сейчас на планах городов. План города разбивают на квадраты, занумерованные с помощью букв и цифр, а на оборотной стороне перечисляются все изображенные улицы в алфавитном порядке и указывают, в квадрате они находятся.
Актуализация знаний.
«Светский разговор»
Учитель: Если можно было бы попасть в 18 или 19 век и очутиться на балу, Вы не испугались бы? А знаете ли Вы, как нужно вести себя на балу, чтобы не попасть впросак? В те времена дамы и кавалеры вели так называемые светские разговоры о лошадях, кошках, собаках, о погоде; пытались блеснуть своими знаниями. Сегодня возможность блеснуть своими знаниями предоставляется и Вам. Будет учитываться время, за которое Вы ответите на предложенные вопросы. В Вашем распоряжении 0, 5 - 1 минута. За правильный ответ команда получает 200 тенге. (1 балл)
«Аукцион знаний»
У каждой команды в наличии 1000 тенге. На аукцион выставляются задачи. Стартовая цена каждого вопроса - 200 тенге.
После того, как учитель прочитает задачу, команда начинает торги. Команда, купившая право на решение (ответа) задачи, получает к имевшейся сумме стоимость ответа. Если команда дала неверное решение (ответ), то из имеющийся на счету команды суммы, вычитывается стоимость ответа. Например, команда, имеющая на счету 600 тенге, покупает право ответа на задачу за 400 тенге и отвечает верно. Теперь на её счету - 1000 тенге. Если команда дала неверный ответ, то на её счету - 200 тенге. В случае если команда покупает вопрос на всю сумму, имеющуюся в наличии на счету команды, и отвечает на вопрос неверно, то они банкрот.
Весь материал - смотрите документ.

 Получите свидетельство
Получите свидетельство Вход
Вход



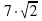 Б)
Б) 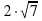 С) 14 Д)28
С) 14 Д)28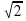 С)
С) 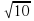 Д) 10
Д) 10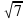 С) (5; 0), R=7 Д) (-5; 0), R=
С) (5; 0), R=7 Д) (-5; 0), R= 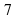 8) Составьте уравнением окружности с центром в точке К (-1; 3) и радиусом, равным 3.
8) Составьте уравнением окружности с центром в точке К (-1; 3) и радиусом, равным 3.








 Урок математики «Прямоугольная система координат. Координаты середины отрезка. Расстояние между двумя точками. Уравнение окружности. Уравнение прямой» (20.91 КB)
Урок математики «Прямоугольная система координат. Координаты середины отрезка. Расстояние между двумя точками. Уравнение окружности. Уравнение прямой» (20.91 КB)
 0
0 2868
2868 505
505 Нравится
0
Нравится
0




