Тема урока: «Пропорция. Основное свойство пропорции»
| Учебная цель: | 1. Ввести определение пропорции. |
| 2. Познакомить учащихся с основным свойством пропорции. |
| 3. Закрепить новые понятия. |
| 4. Научить использовать основное свойство при решении задач и уравнений. |
| 5. Привести примеры использования пропорции в повседневной жизни. |
| 6. Показать связь математики с химией, физикой, изобразительным искусством и т.д. |
| Воспитательная цель: | 1. Воспитание единого научного мировоззрения. |
| 2. Развивать аккуратность при оформлении записей. |
| Развивающая цель: | 1. Активизация интеллектуальной деятельности учащихся. |
| 2. Повышение интереса к математике. |
| 3. Развитие у учащихся логического мышления. |
Оборудование: Две доски, 4 плаката, сигнальные карточки, карточки с Индивидуальными заданиями, карточки с самостоятельной работы для закрепления материала, учебник «Математике, 6» (авторы: Н.Я. Виленкин, А.С. Чесноков и др.).
ХОД УРОКА
I. Организационный момент
Вступительное слово учителя. И ознакомление учащихся с планом урока :
| II. | Проверка домашнего задания | 2 мин. |
| III. | Вопросы на повторение | 3 мин. |
| IV. | Решение задач на повторение | 4 мин. |
| V. | Устный счет | 5 мин. |
| VI. | Восприятие и усвоение нового материала | 10 мин. |
| VII. | Осмысление и закрепление нового материала | 5 мин. |
| VIII. | Самостоятельная работа по вариантам | 7 мин. |
| IX. | Подведение итогов урока | 2 мин. |
| X. | Домашнее задание | 2 мин. |
II. Проверка домашнего задания
1. Перед уроком один из учащихся (консультант) проверяет наличие домашнего задания у всех учащихся класса.
2. Перед уроком решение домашнего задания написано на доске.
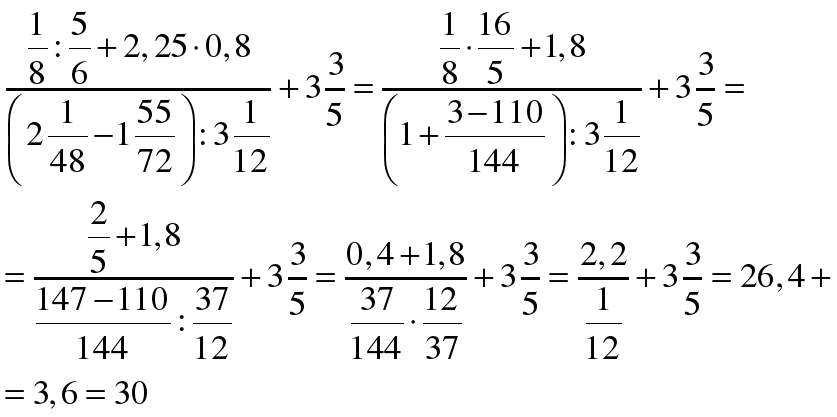
3. На уроке выясняем вопросы, которые возникли во время выполнения домашнего задания и решаем их.
4. Собрать тетради на проверку.
III. Вопросы на повторение (работа по таблице «Отношения и их свойства»)
1. Что называется отношением двух чисел?
2. Что показывает отношение двух чисел?
3. Как узнать, какую часть числа а составляет от числа в?
4. Какие свойства отношений вы знаете?
5. Какие отношения называют взаимно обратными?
IV. Решение задач на повторение
Задача: За первый час машина проехала 60 км пройденного пути, что составляет 12%. Какая длина пройденного пути?
В сего – ?
сего – ?
За первый час – 60 км = 12% от
Решение:
12% = 0,12
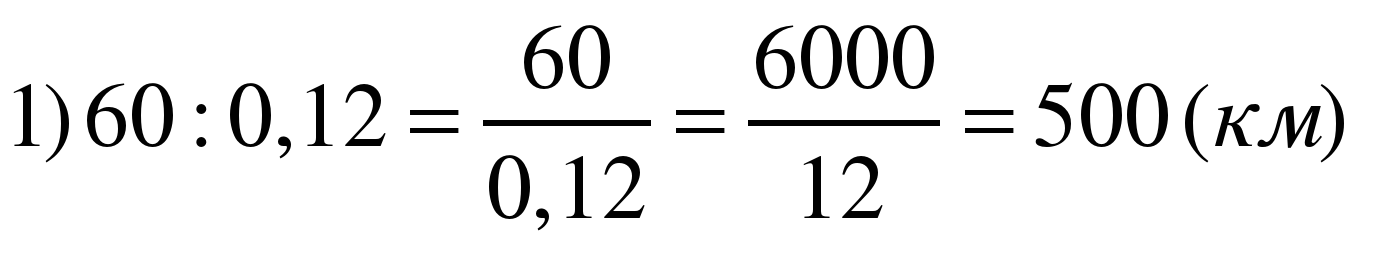 - проехала машина
- проехала машина
Ответ: 500 км
V. Устный счет (тема урока в игровой форме – верный ответ предложенного примера – дает буквы ключевого слова «Пропорция»)
Примеры для устного счета:
№1. 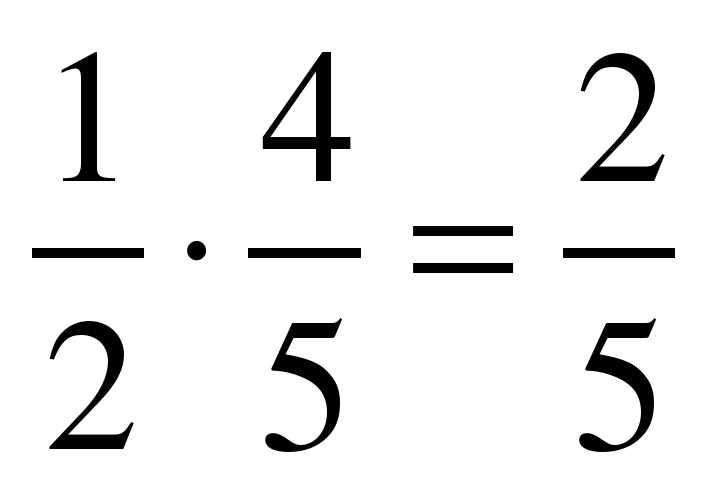 (П) №4.
(П) №4. 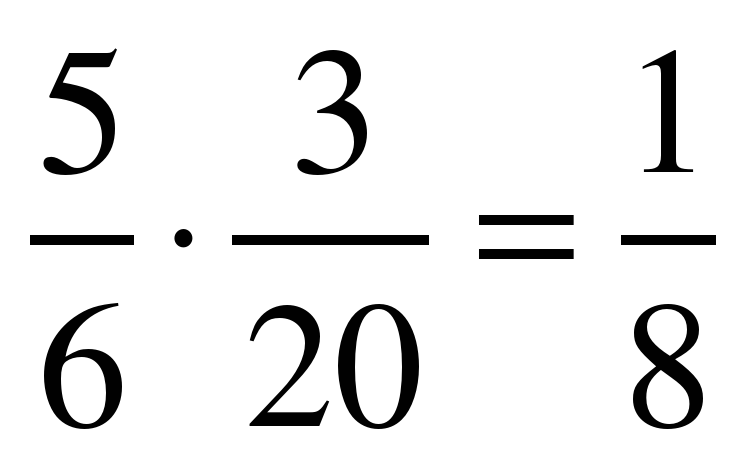 (П) №7.
(П) №7. 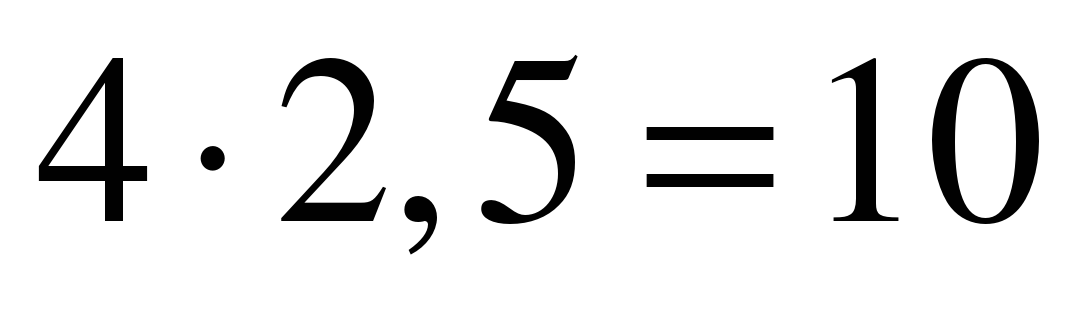 Ц)
Ц)
№2. 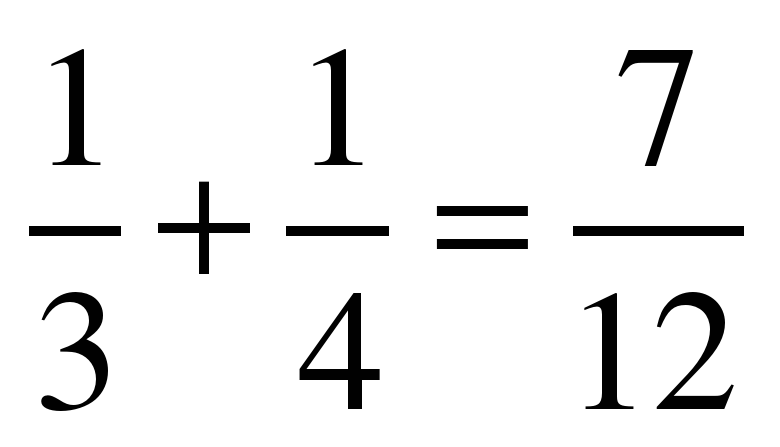 (Р) №5.
(Р) №5. 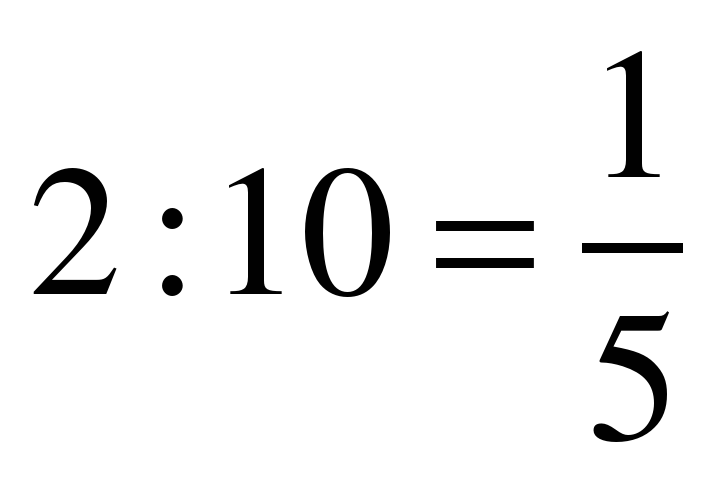 (О) №8.
(О) №8. 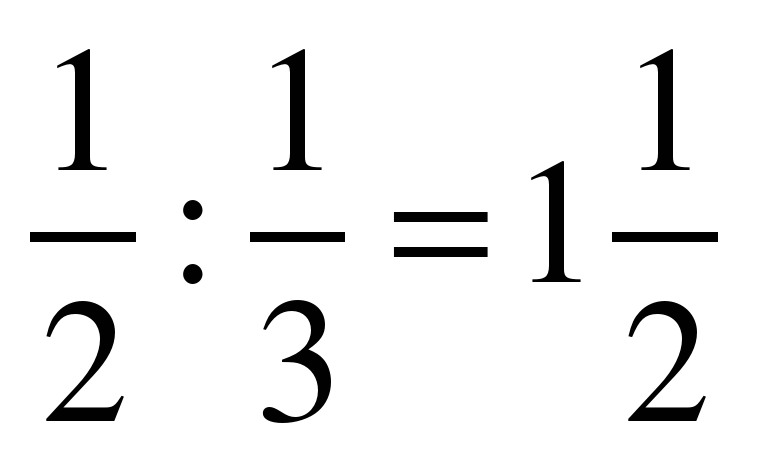 (И)
(И)
№3. 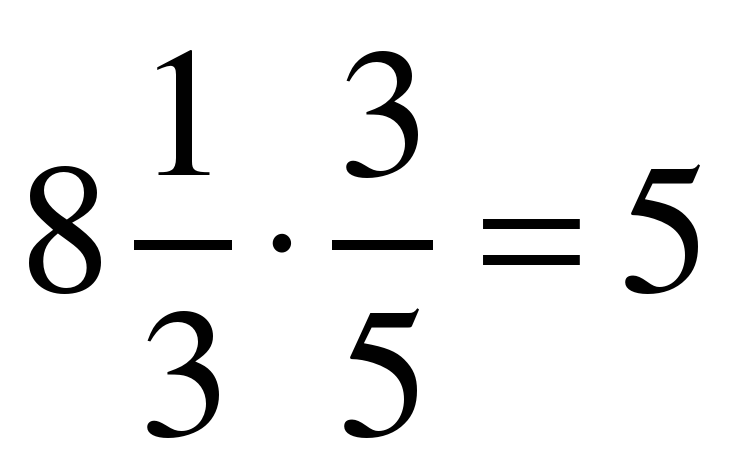 (О) №6.
(О) №6. 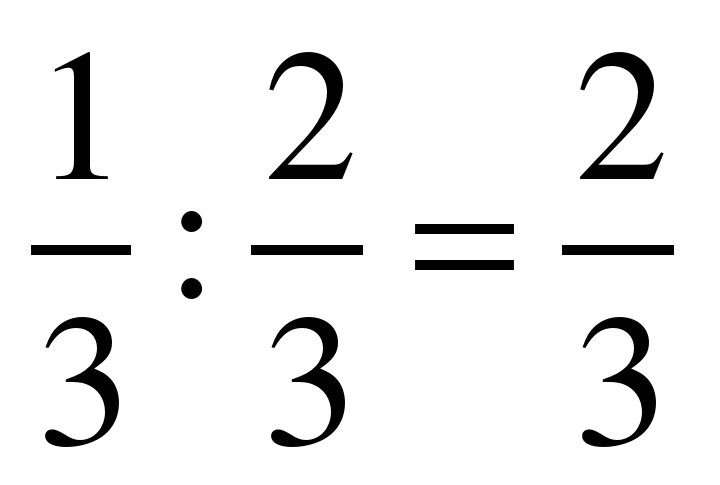 (Р) №9.
(Р) №9. 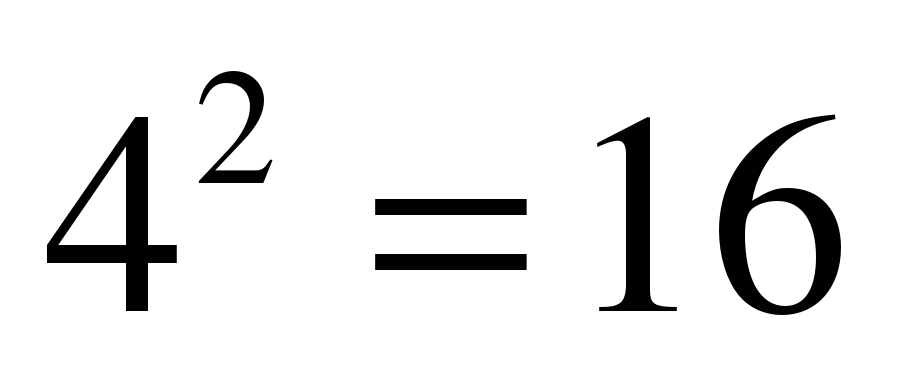 (Я)
(Я)
| № | Р | А | О | К | Ц | Я | Б | П | И |
| 1 | 1,2 | 0 | 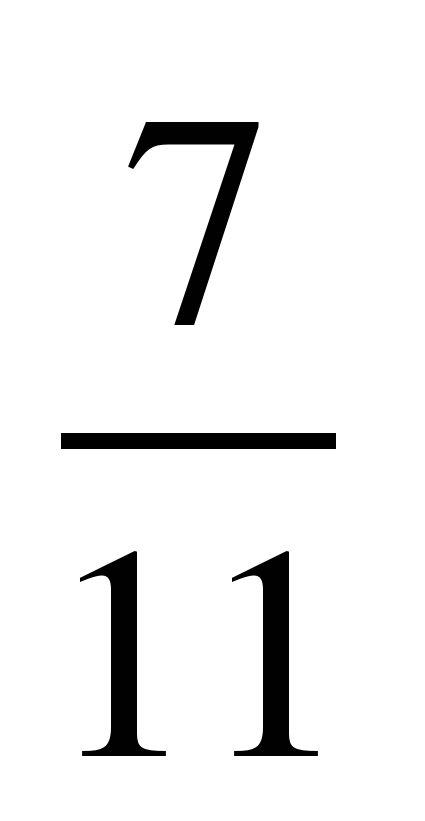
| 7 | 0,4 | 218 | 5 | 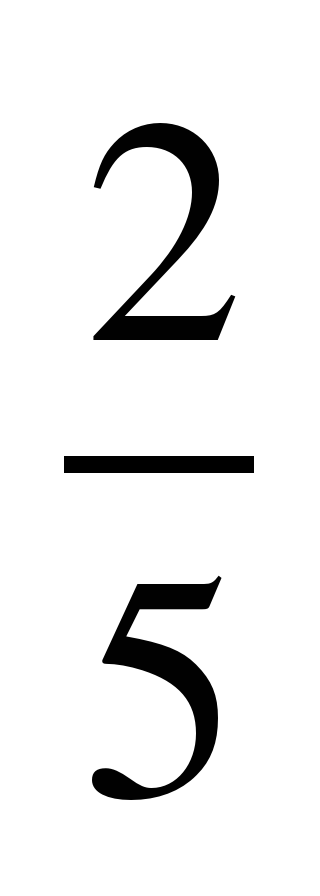 | 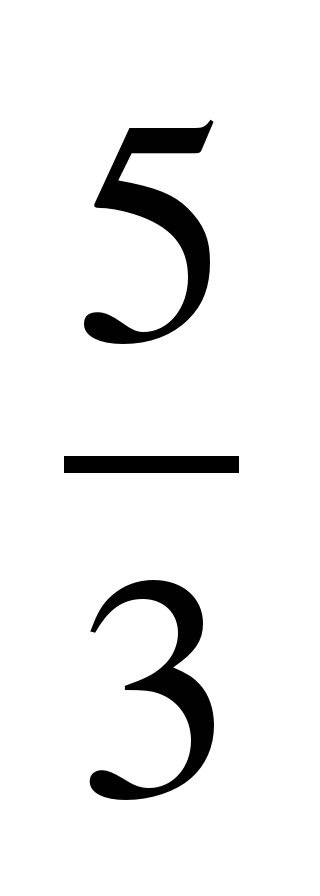
|
| 2 | 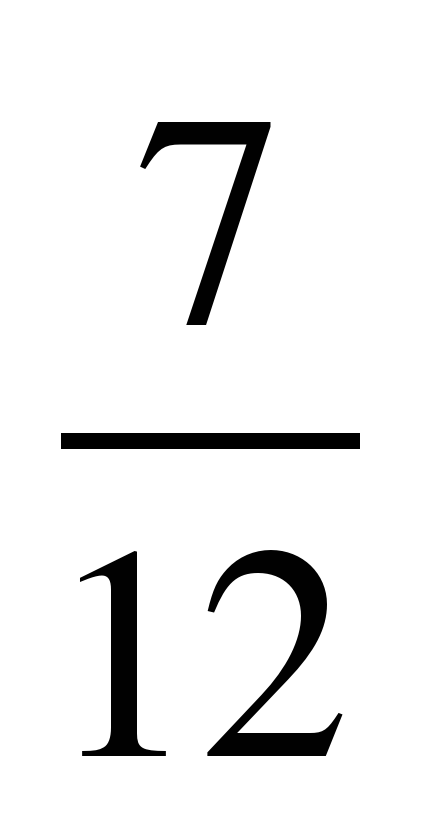 | 3 | 2 | 1 | 11 | 0,53 | 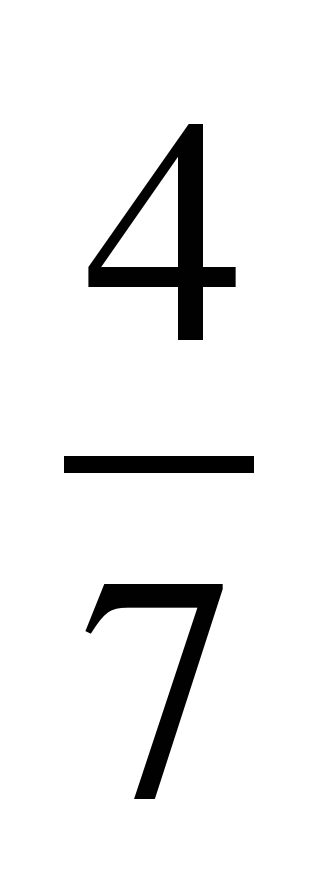 | 30,3 | 0,18 |
| 3 | 3 | 15 | 5 | 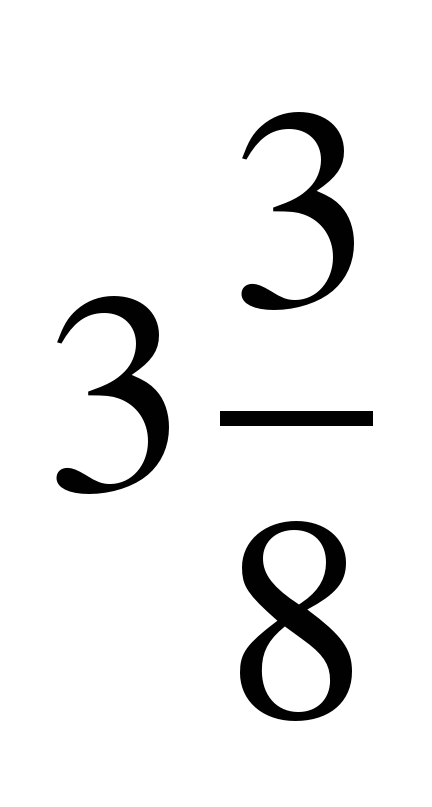
| 0 | 18 | 7,09 | 4 | 364 |
| 4 | 19 | 0,26 | 34 | 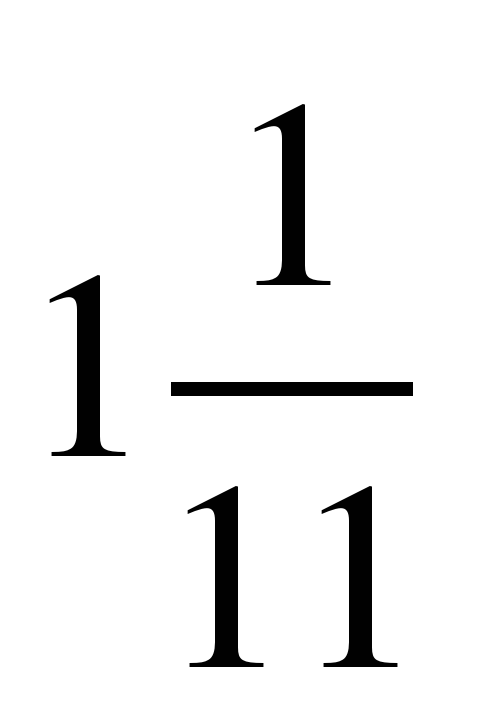 | 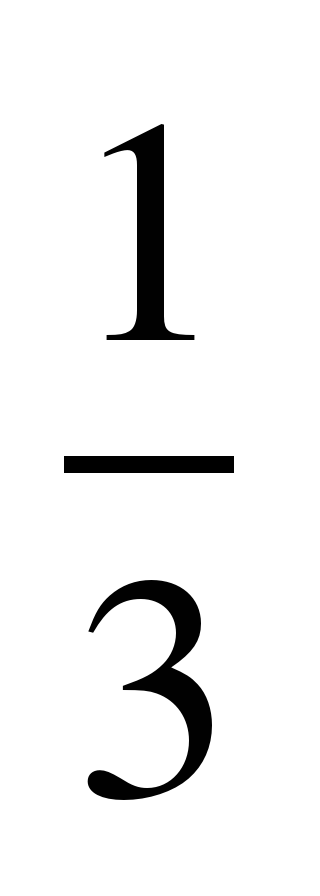
| 4 | 9 | 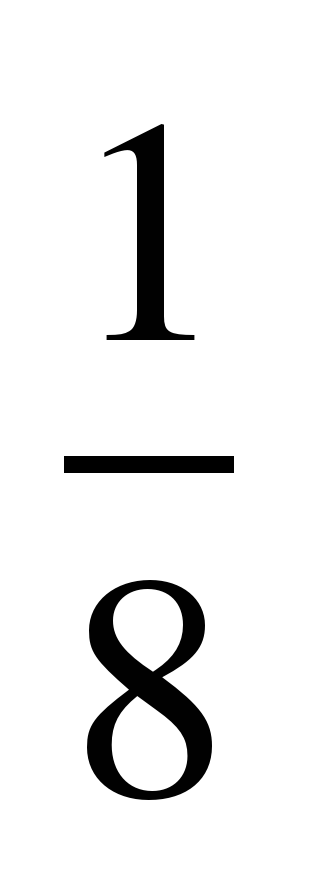
| 8 |
| 5 | 10 | 0,13 | 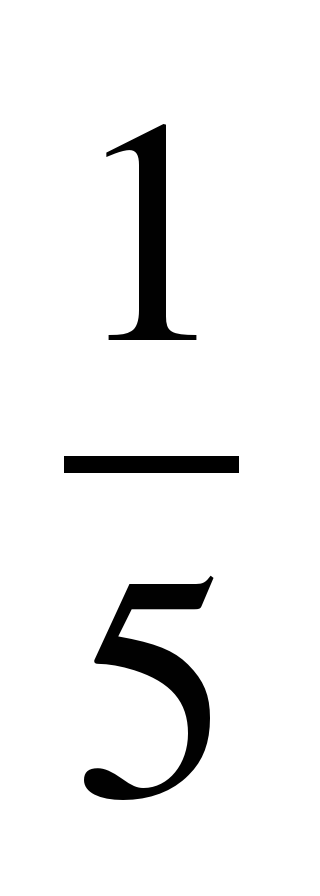
| 100 | 0,4 | 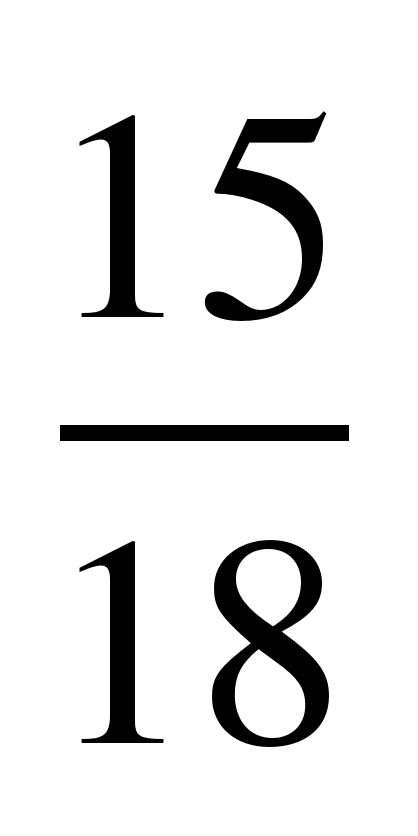
| 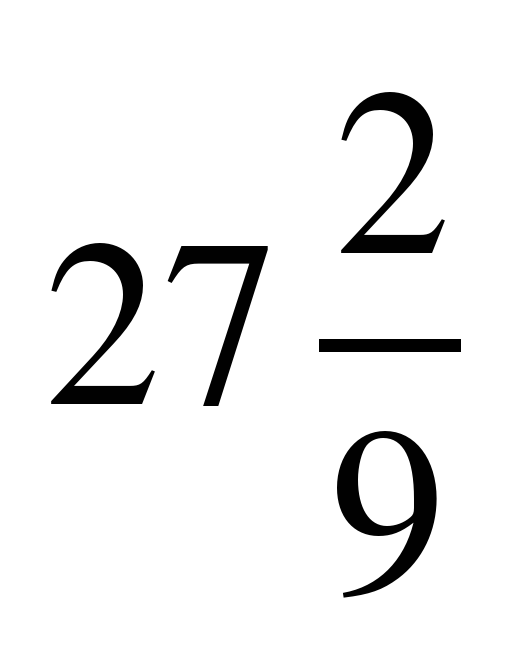
| 9 | 28 |
| 6 | 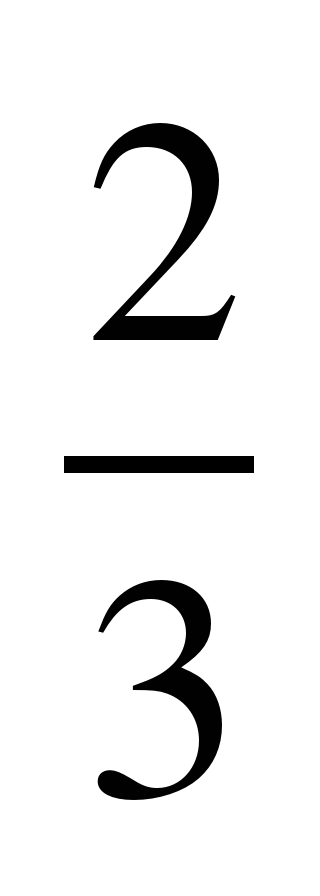 | 36 | 0,3 | 101 | 0,1 | 7 | 76 | 4,3 | 15 |
| 7 | 2 | 34 | 0,5 | 88 | 10 | | 0,2 | 9 | 3 |
| 8 | | | 5 | 7 | 0,15 | 11 | 100 | 0,3 | |
| 9 | 0 | 100 | 6 | 7 | 15 | 16 | 17 | 0,6 | 17 |
VI. Восприятие и усвоение нового материала
1. Среди данных отношений выбрать те, которые равны между собой
15 : 20; 42 : 7; ;
18 : 6; 2 : 1; 12 : 6;
6 : 8; 24 :4 ; 5 : 7.
Решение:
15 : 20 = 3 : 4; 42 : 7 = 6 : 1; ;
18 : 6 = 3 : 1; 2 : 1 = 2 : 1; 12 : 6 = 2 : 1;
6 : 8 = 3: 4; 24 :4 = 6 : 1; 5 : 7 = 5 : 7.
Ответ: 15 : 20 = 6 : 8; 42 : 7 = 24 : 4; 2 : 1 = 12 : 6.
2. Равенства такого вида называют пропорцией.
Определение: Равенство двух отношений называют пропорцией.
С помощью букв пропорцию записывают так:
или
Читается:
«Отношение а к b равно «а так относится к b, как c
отношению c к d» относится к d»
3. Числа а, b, c и d называются членами пропорции, причем b и c Называют средними членами, а а и d – крайними членами пропорции.
4. Основное свойство пропорции. Если пропорция верна, то произведение крайних членов равно произведению средних членов. Если а : b = c : d – истина, то b ∙ c= а ∙ d .
5. Верно и обратное утверждение. Если в верной пропорции поменять местами средние члены, то получившиеся новые пропорции тоже верны.
6. Используя основное свойство пропорции, можно найти её неизвестные члены, если все остальные члены известны.
Пример
2 : а = 3 : 12, ,
3а = 2 ∙ 12, или ,
3а = 24, а = 8.
а = 8.
7. Историческая справка.
«Пропорция» с латинского (proportio) обозначает «имеющий правильное соотношение частей». Пропорции начали изучать в Древней Греции. С пропорциями связывали представления о красоте, порядке и гармонии (строительство, музыка, рисование и т.д.). Еще в IV веке до н.э. древнегреческий ученый Евклид Досконально изложил теорию отношений и пропорций. В наше время ни одна серьезная наука не может обойтись без пропорций (физика, химия, изобразительное искусство).
VII. Осмысление и закрепление нового материала
Задание №1. (по плакату «Задание от клоуна»)
Клоун составил пропорции
1) 3 : 6 = 2 : 4; 5) 6 : 2 = 4 : 6;
2) 4 : 6 = 2 : 3; 6) 6 : 4 = 3 : 2;
3) 3 : 6 = 4 : 2; 7) 6 : 3 = 4 : 2;
4) 6 : 3 = 2 : 4; 8) 8 : 4 = 2 : 3.
Все ли пропорции составлены верно?
Задание№2.
Решить задачу п. IV, используя пропорции.
Решение:
х км – 100%
60 км – 12%
По условию задачи составляем пропорцию.
,
,
х = 500.
Ответ: Машина проехала 500 км.
VIII. Самостоятельная работа по вариантам
Вариант 1.
Из 18 тонн железной руды выплавляют 100 тонн железа. Сколько железа можно получить из 36 тонн руды?
Решение:
18 т – 10 т
36 т - ?
По условию задачи составляем пропорцию.
,
,
х = 20.
Ответ: Можно получить 20 тонн железа.
Вариант 2.
В семенах льна содержится 40% масла. Сколько масла содержится в 80 кв семян льна?
Решение:
80 кв. – 100%
? – 40 %
По условию задачи составляем пропорцию.
,
,
х = 32.
Ответ: Содержится 32 кг масла.
IX. Подведение итогов урока
А) Вопросы для закрепления материала.
1. Что такое пропорция?
2. Сформулируйте основное свойство пропорции?
3. Как называются члены пропорции?
4. Приведите примеры пропорций.
Б) Сообщение и мотивация оценок.
В) Благодарность за плодотворную совместную работу.
X. Домашнее задание
1. Выучить определение пропорции и ее основное свойство. (§4, п. 21).
2. Выполнить №761 (а, в), №762

 Получите свидетельство
Получите свидетельство Вход
Вход



 сего – ?
сего – ?








 Урок математики "Пропорция. Основное свойство пропорции" (0.17 MB)
Урок математики "Пропорция. Основное свойство пропорции" (0.17 MB)
 0
0 2420
2420 324
324 Нравится
0
Нравится
0



