Урок-калейдоскоп «Куб»

У Р О К – К А Л Е Й Д О С К О П

ВСТУПИТЕЛЬНОЕ СЛОВО

На уроке мы с вами разберём: изображение и определение куба, элементы и свойства куба, исторические факты и находки. В задачах рассмотрим углы, сечения, диагонали куба и практическое применение кубов.

Нам предстоит рассмотреть необычное применение кубов. А загадка позволит вспомнить разные геометрические понятия и постичь народную мудрость.

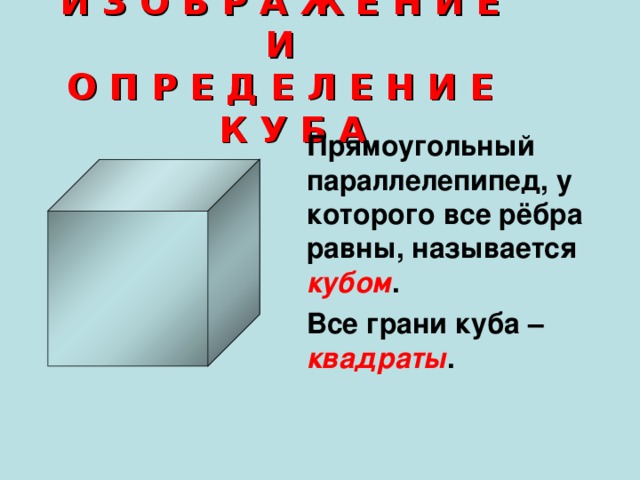
И З О Б Р А Ж Е Н И Е И О П Р Е Д Е Л Е Н И Е К У Б А

Прямоугольный параллелепипед, у которого все рёбра равны, называется кубом .

Все грани куба – квадраты .

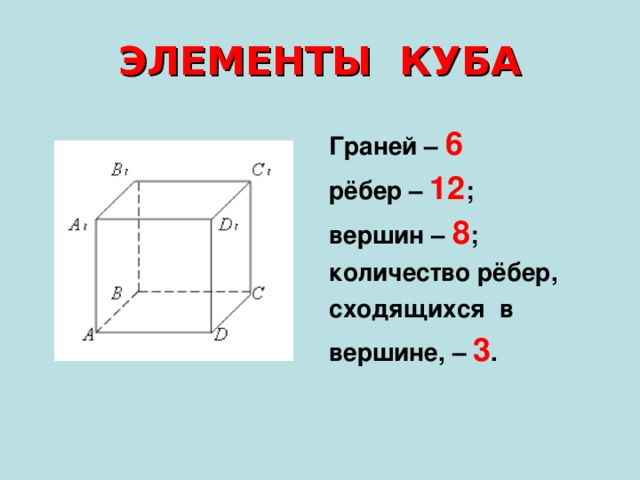
ЭЛЕМЕНТЫ КУБА

Граней – 6

рёбер – 12 ;

вершин – 8 ;

количество рёбер,

сходящихся в

вершине, – 3 .

СВОЙСТВА КУБА

Длина ребра – а

Длина диагонали – d = a

Радиус описанной сферы – R =

Радиус вписанной сферы – r =

Объём – V = a 3

Площадь боковой поверхности – S бок = 4 a 2

Площадь полной поверхности – S пол = 6 a 2

Ф А К Т Ы И Н А Х О Д К И

• Куб относится к правильным многогранникам.
• Куб также называют гексаэдром.
• Форму гексаэдра имеют кристаллы поваренной соли, пирита, сильвина и некоторые алмазы.

• Развёрнутый гексаэдр

И З И С Т О Р И И

• Про куб знали ещё древнегреческие геометры.
• В философии Платона: «Куб символизирует Землю, как самый «устойчивый».
• В «Началах» Евклида предлагается такое определение: «Куб есть тело, ограниченное шестью равными квадратами».
• Античные учёные считали, что атомы Земли имеют форму гексаэдра.

П О В Т О Р Е Н И Е

З а д а ч а 1

На рисунке изображён куб АВСDA 1 B 1 C 1 D 1 . Установите соответствие между

заданными углами (1-10) и их градусными мерами (А-Г).

1. Угол между прямыми АA 1 и DC 1 .

2. Угол между прямыми ВD и A 1 C 1 .

3. Угол между прямыми АB 1 и A 1 D .

4. Угол между прямыми ВB 1 и DD 1 .

5. Угол между прямой C 1 С и плоскостью АВС .

6. Угол между прямой A 1 B 1 и плоскостью СDD 1 .

7. Угол между прямой B 1 C и плоскостью A 1 B 1 C 1 .

8. Угол между плоскостями АСC 1 и ВDD 1 .

9. Угол между плоскостями АDC 1 и A 1 B 1 C 1 .

10. Угол между плоскостями АDD 1 и ВСC 1 .

А – 0 º; Б – 45º; В – 60º; Г – 90º

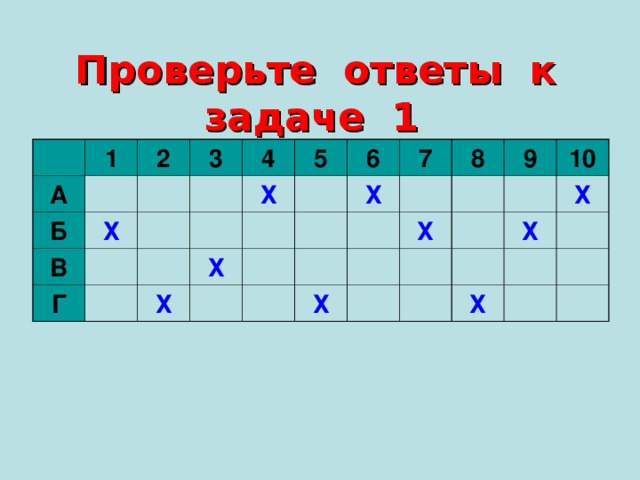
Проверьте ответы к задаче 1

1

А

2

Б

3

Х

В

4

Г

5

Х

Х

6

Х

7

Х

8

9

Х

Х

10

Х

Х

Х

П О В Т О Р Е Н И Е

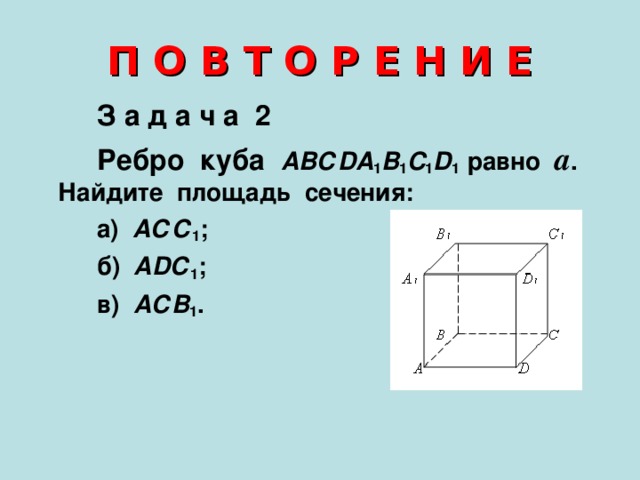
З а д а ч а 2

Ребро куба АВСDA 1 B 1 C 1 D 1 равно а . Найдите площадь сечения:

а) АСС 1 ;

б) А DС 1 ;

в) АСВ 1 .

ПРИМЕНЕНИЕ КУБОВ

Бумажное чудо. Кто бы мог подумать, что из обычного листа бумаги может появиться чудо. И это чудо могут сделать своими руками не только дети, но и взрослые. Поделки из бумаги могут оказаться интересными элементами интерьера, подарками родным и друзьям. Для этого существуют искусства пластической разработки объёмов, оригами, ажурной бумаги, бумажных туннелей, фонарей, рисования, применимые для кубов.

ПЛАСТИЧЕСКАЯ РАЗРАБОТКА ОБЪЕМОВ

Для пластической разработки объемов можно использовать различные композиционные приемы, например, метроритмические членения и цвет. В некоторых случаях поверхности объемной формы могут быть усложнены применением дополнительных поверхностей различной кривизны: сферических, двояковыпуклых и т.д.

КУБЫ - ОРИГАМИ

Оригами – это искусство складывания бумаги,

создание различных фигурок и декоративных

вещей из этого простого и доступного всем

материала. Оставаясь неотъемлемой частью

определённых японских церемоний и ритуалов,

оригами распространилось по всему миру,

доставляя радость и

принося пользу миллионам

людей. Оно используется в

реабилитационный период

после некоторых болезней,

очень полезно в

образовательных целях.

ПОДВИЖНЫЕ КУБЫ - ОРИГАМИ

Первый и наиболее простой вариант, который состоит из 9 кубов и соответственно из 54-х модулей, по 6 штук на один куб. Данная модель может подобно калейдоскопу менять свою форму по окружности. Для этого достаточно просто расправить и снова сложить кубики .

3D подвижные кубы сонобе

(второй вариант)

Данная модель отличается тем, что кубов у нас стало 16 и соответственно понадобится 96 модулей. Данная модель может вращаться во все стороны, правда со значительными ограничениями, но смотрится волшебно.

КВИЛЛИНГ - КУБЫ

Одним из последних модных направлений в рукоделии является квиллинг . Для детей этот вид занятий имеет не только развлекательный характер, но и несёт в себе огромную пользу. Так как работая с мелкими деталями, хорошо развивается мелкая моторика рук, что очень важно для развития ребёнка в целом. Кроме этого хорошо тренирует внимание и умение концентрировать внимание. Для людей старшего возраста квиллинг – это хорошее хобби и отдых, который приносит наслаждение.

Шкатулки, подарочные коробки

АЖУРНЫЕ КУБЫ

Тот, кто впервые видит изделия, выполненные в виде резных кружев из обычной бумаги, всегда удивляется, что такую красоту несложно создать своими руками. Каждый может освоить ажурное вырезание из бумаги. Главное — терпение, усидчивость и желание сделать шедевр своими руками. Очень эффектно выглядит объемное ажурное вырезание из бумаги.

Подсвечники, коробочки для подарков, бонбоньерки

КУБЫ - ТУННЕЛИ

Оригинальное английское название этой техники  tunnelbook , что можно перевести как книжный или  бумажный туннель . Суть техники хорошо прослеживается из английского названия  tunnel  —  туннель  —  сквозное отверстие . Многослойность составляемых «книжек» ( book ) хорошо передает ощущение туннеля. Возникает трёхмерная открытка. Она чем-то сродни оригами, т.к. направлена на складывание бумаги определённым образом.

Интересные миниатюрные кубы-туннели 8 × 8 см.

БУМАГОПЛАСТИКА В КУБЕ

Бумагопластика в кубе – очень увлекательное занятие. Необходимо заполнить пространство куба элементами из бумаги. Здесь мы наблюдаем уникальную возможность бумаги: трансформироваться из плоского листа в объем. Детям данное занятие очень понравилось. Фантазия детская безгранична. Можно рассматривать и удивляться бесконечно. Все справляются с работой на отлично. Занятие по бумагопластике вырабатывает усидчивость, аккуратность, желание создавать красоту, развивает фантазию, пространственное и ассоциативное мышление.

РАЗРИСОВАННЫЕ КУБЫ

Превратить двухмерный рисунок в трехмерный объект очень просто. Распечатайте или нарисуйте сами любой шаблон куба, нарисуйте абстрактный рисунок на поверхности шаблона, раскрасьте его. А затем склейте куб. Ребенок, несомненно, оценит это воплощение, а тот, кто постарше, и самостоятельно сможет нарисовать на кубике абстракцию. Оптические иллюзии замечательно подходят для этого проекта.  

ФОНАРИКИ - КУБЫ

Китайские бумажные фонарики – это одновременно украшение и талисман. Их используют не только для декорирования праздников. Согласно древним легендам, бумажные фонарики способны отпугнуть демонов, привлечь удачу, а влюбленным, которые разругались, вернуть утраченное счастье. Глядя на очаровательное мерцание огоньков в фонариках, действительно хочется в это верить.

З А К Р Е П Л Е Н И Е

З а д а ч а 3

Ребро куба АВСDA 1 B 1 C 1 D 1 равно 2 см . Чему равна площадь треугольника АDC 1 ?

З а д а ч а 4

Диагональ основания куба а . Чему равна диагональ куба?

З а д а ч а 5

Диагональ куба равна а . Чему равен объём куба?

ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ

З а д а ч а 6

Три латунных куба с рёбрами 3 см, 4 см и 5 см переплавили в один куб. Какое ребро этого куба?

З а д а ч а 7

Металлический куб имеет внешнее ребро 10,2 см и массу 514,15 г. Толщина стенок равна 0,1 см. Найдите плотность материала, из которого сделан куб.

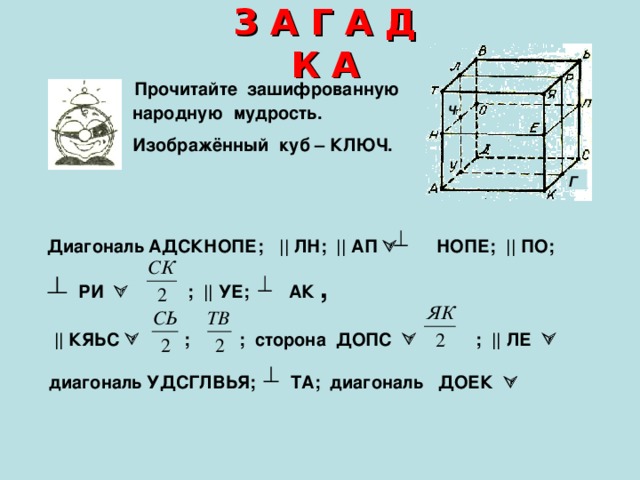
З А Г А Д К А

Прочитайте зашифрованную

народную мудрость.

Изображённый куб – КЛЮЧ.

Диагональ АДСКНОПЕ; || ЛН; || АП  НОПЕ; || ПО;

РИ  ; || УЕ; АК ,

|| КЯЬС  ; ; сторона ДОПС  ; || ЛЕ 

диагональ УДСГЛВЬЯ; ТА; диагональ ДОЕК 

Ч

Г

Н А Р О Д Н А Я М У Д Р О С Т Ь

Корень ученья горек , да плод его сладок

П О Д В Е Д Е Н И Е И Т О Г О В

На уроке были обобщены знания, связанные с понятием куба и его применением в бумаге.