Тема урока: «Примеры комбинаторных задач» 9 кл. 28.02.2019 День открытых дверей в школе
Цель урока: познакомить учащихся с разделом математики – комбинаторикой. Показать решение некоторых комбинаторных задач.
Задачи урока:
Образовательные:
Развитие умения решать комбинаторные задачи методом полного перебора вариантов; используя правило умножения;
Выработка умения применять математическую теорию в конкретных ситуациях;
Знакомство учащихся с элементами гуманитарного знания, связанного с математикой.
Развивающие:
Развитие умения самостоятельно выбирать способ решения и умения обосновать выбор;
Развитие умения решать задачи путём только логических рассуждений.
Воспитательные:
Воспитывать чувство ответственности за качество и результат выполняемой работы;
Прививать сознательное отношение к труду;
Формировать ответственность за конечный результат.
Оборудование урока:
Учебник
Презентация Рower Point.
Листочки для самостоятельной работы.
Карточки для проведения рефлексии.
Ход урока:
В науке и практике часто встречаются задачи, решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитать число комбинаций.
Такие задачи называются комбинаторными задачами, а раздел математики, в котором рассматриваются эти задачи, называется комбинаторикой.
Слово «комбинаторика» происходит от латинского слова combinate, которое означает «соединять», «сочетать». С комбинаторными задачами люди столкнулись в глубокой древности. В Древнем Китае увлекались составлением магических квадратов. В Древней Греции занимались теорией фигурных чисел. Комбинаторные задачи возникли и в связи с такими играми, как шашки, шахматы, домино, карты, кости и т.д. Комбинаторика становится наукой лишь в 18 в. – в период, когда возникла теория вероятности.
Рассмотрим такой
пример1. Несколько стран в качестве символа своего государства решили использовать флаг в виде трех горизонтальных полос одинаковых по ширине, но разных по цвету: белый, синий, красный. Сколько стран могут использовать такую символику при условии, что у каждой страны свой, отличный от других, флаг?
-Решение будем искать с помощью «дерева возможных вариантов».
Посмотрим на левую «веточку», идущую от «флага», пусть верхняя полоса – белого цвета, тогда средняя полоса может быть синей или красной, а нижняя – соответственно, красной или синей. Получилось два варианта цветов полос флага: белая, синяя, красная и белая, красная, синяя.
Пусть теперь верхняя полоса – синего цвета, это вторая «веточка».
Тогда средняя полоса может быть белой или красной, а нижняя - соответственно, красной или белой. Получилось еще два варианта цветов полос: синяя, белая, красная и синяя, красная, белая.
Аналогично рассматривается случай для верхней полосы красного цвета.
Получается еще два варианта: красная, белая, синяя и красная, синяя, белая.
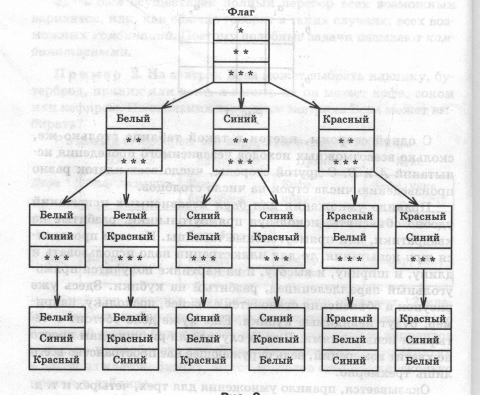
Всего 6 комбинаций.
Ответ: 6. - Построенная схема действительно напоминает дерево, только перевернутое. Поэтому ее называют «деревом возможных вариантов».
Задача. По окончании деловой встречи специалисты обменялись визитными карточками. Сколько всего визитных карточек было роздано, если специалистов было а) трое ; б) четверо ; в) пятеро?
N=3 N=6 N=10
2. Сколько чётных двузначных чисел можно составить из цифр 0,1,2,4,5,9.
Ответ:15 чисел (5·3)
- Составим таблицу: слева от 1 – го столбца поместим первые цифры искомых чисел, сверху – вторые цифры этих чисел (чётные цифры, тогда столбцов будет три).
Пример 2. На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром.
Из скольких вариантов завтрака Вова может выбирать?Решение.
|
| Плюшка | Бутерброд | Пряник | Кекс |
| Кофе | Кофе Плюшка | Кофе Бутерброд | Кофе Пряник | Кофе Кекс |
| Сок | Сок Плюшка | Сок Бутерброд | Сок Пряник | Сок Кекс |
| Кефир | Кефир Плюшка | Кефир Бутерброд | Кефир Пряник | Кефир Кекс |
Решение: КП КБ К Пр КК
СП СБ С Пр СК
К-р П К-р Б К-р Пр К-р К
Ответ: 12 вариантов.
Всего вариантов столько же, сколько клеток в таблице. Ответ:12 (4·3=12)
- Однако составлять такие таблицы для каждой задачи, занимает время.
А чтобы решить такую задачу быстрее, можно воспользоваться правилом умножения.
Во всех задачах был осуществлён перебор всех возможных вариантов или комбинаций. Поэтому эти задачи называют комбинаторными.
-Действительно при получении любой комбинации мы составляем её из отдельных элементов последовательно соединяя их друг с другом. С этой точки зрения: число – это комбинация цифр, слово – это комбинация букв, меню – это комбинация блюд.
- Во всех предложенных задачах для подсчёта числа комбинаций мы использовали простой способ подсчёта – прямое перечисление (опираясь на «дерево возможных вариантов», таблицу, кодирование). Но способ перебора возможных вариантов далеко не всегда применим, ведь количество комбинаций может исчисляться миллионами.
-Здесь на помощь приходят несколько замечательных комбинаторных правил, которые позволяют подсчитать количество комбинаций без их прямого перечисления.
Правило умножения.
Пусть имеется n элементов и требуется выбрать из них один за другим к элементов. Если первый элемент m1 выбрать n1 способами, после чего
второй элемент m2 выбрать n2 способами из оставшихся, затем
третий элемент m3 выбрать n3 способами из оставшихся и т.д.,
то число способов могут быть выбраны все к элементов, равно произведению
Для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В , следует перемножить число всех исходов испытания А и число всех исходов испытания В.
Закрепление. Стр.174 №714
Решение:
-Что бы указать все обеды из двух блюд, будем рассуждать так:
Выберем одно блюдо (борщ) и будем добавлять к нему поочерёдно разные вторые блюда, получая пары: Б г; б к; б с; б п (4 пары).
Теперь в качестве первого блюда выберем рассольник и будем добавлять к нему поочерёдно разные вторые блюда: Рг; р к; р с; р п (4 пары).
Согласно правилу комбинаторного умножения всего обедов: 2*4=8.
- Построив дерево возможностей, получим 8 вариантов.
Ответ: б г; б к; б с; б п; р г; р к; р с; р п.; получим 8 разных обедов из двух блюд.
№ 716 Работа у доски.
Решение:
Из условия ясно, что порядок выбора имеет значение: АВ означает, что посетитель вошёл через А и вышел через В, а ВА означает, что вошёл через В, а вышел через А.
первый вход, получаем 3 пары: АВ, АС, АД.
второй вход : ВА, ВС, ВД.
третий вход :СА, СВ, СД.
четвёртый вход: ДА, ДВ, ДС.
Общее количество способов выбора: 4*3=12 (к каждому из 4 входов мы дописывали 3 других).
Замечание. По правилу произведения:
первый выбор (через какой вход войти) можно сделать 4 способами (А, или В, или С, или Д);
после этого второй выбор (через какой вход войти) можно сделать 3 способами ( любой вход, кроме того, через который вошли). Общее количество выбора равно 4*3=12.
Ответ: 12 способов.
№718
Решение. а) Выбираем поочерёдно: 16, 18, 61, 68, 81, 86. Всего 6 различных чисел
№ 721. Работа у доски.
Решение.
Каждая пара участников играла между собой только один раз, порядок выбора не имеет значения (когда Иванов играл с Петровым, это то же самое, что Петров играл с Ивановым).
Выбрать первого участника партии можно 9 способами, а второго- 8 оставшимися способами;
по правилу произведения всего можно образовать 9*8=72 пары,
но в это число каждая пара входит дважды: сначала Иванов-Петров, затем Петров- Иванов.
Поскольку порядок выбора не имеет значения, то общее количество партий равно .
Ответ: 36 партий.
Итог урока. Рефлексия.
- А теперь поделись своим настроением.
Домашнее задание: №715,717,723, найти сообщение из истории комбинаторики

 Получите свидетельство
Получите свидетельство Вход
Вход












 Урок алгебры в 9 классе по теме: «Примеры комбинаторных задач» (189 KB)
Урок алгебры в 9 классе по теме: «Примеры комбинаторных задач» (189 KB)
 0
0 353
353 27
27 Нравится
0
Нравится
0


