Урок алгебры в 9 классе по теме Последовательности

Урок алгебры в 9 классе

«Числовые последовательности»

Ты можешь стать умнее тремя путями:

путем опыта – это самый горький путь; путем подражания – это самый легкий путь; путем размышления – это самый благородный путь.

Китайская пословица.

Повторение

Готовимся

к ГИА

1. Расположите в порядке убывания числа: 0,1327; 0,014; 0,13

А) 0,1327; 0,014; 0,13

Б) 0,014; 0,13; 0,1327

В) 0,1327; 0,13; 0,014

Г) 0,13; 0,014; 0,1327

2. При каком из указанных значений х выражение

не имеет смысла?

А) при х = -2

Б) при х = -1

В) при х = 1

Г) при х = 0

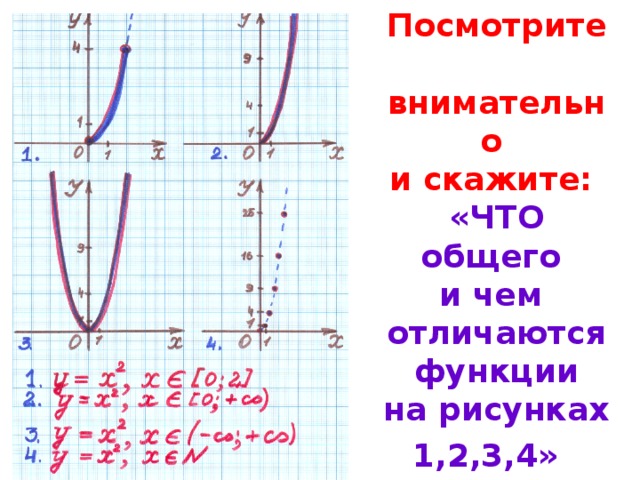
Посмотрите внимательно и скажите: «ЧТО общего и чем отличаются функции на рисунках 1,2,3,4»

Последовательностью называется

бесконечное

множество пронумерованных элементов.

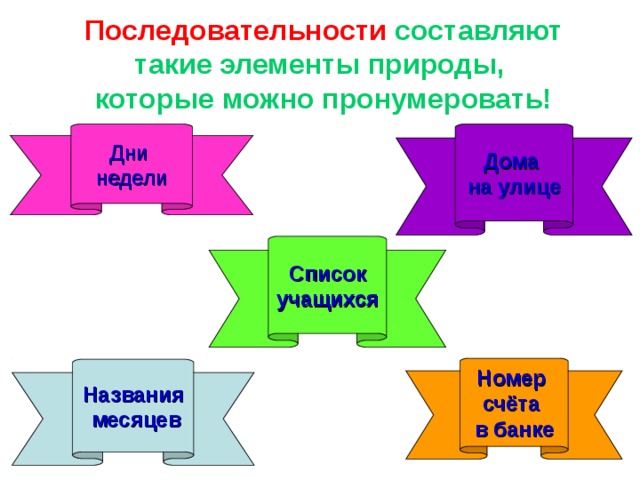
Последовательности составляют такие элементы природы, которые можно пронумеровать!

Дни

недели

Дома

на улице

Список

учащихся

Номер

счёта

в банке

Названия

месяцев

• 1,3,5,7,9,…

• 2,4,6,8,10,…

• 5,10,15,20,25,…

Число + последовательность

_____________________

числовая последовательность

Тема урока:

«Числовые

последовательности»

Рассмотренные числовые ряды –

примеры числовых последовательностей

Обозначают члены последовательности так

а 1 ; а 2 ; а 3 ; а 4 ; … а n

1, 2, 3, 4, … , n - порядковый номер члена последовательности.

(а n ) - последовательность,

(а n ) - последовательность, а n − n-ый член

последовательности

(а n ) - последовательность, а n − n-ый член

последовательности

а n-1 − предыдущий член последовательности

(а n ) - последовательность, а n − n-ый член

последовательности

а n-1 − предыдущий член последовательности

а n+1 − последующий член последовательности

Понятие числовой последовательности возникло и развилось задолго до создания учения о функции. Вот примеры бесконечных числовых последовательностей, известных еще в древности:

1, 2, 3, 4, 5,… - последовательность натуральных чисел;

2, 4, 6, 8, 10,… - последовательность четных чисел;

1, 3, 5, 7, 9, … - последовательность нечетных чисел;

1, 4, 9, 16, 25, … - последовательность квадратов натуральных

чисел;

2, 3, 5, 7, 11, … - последовательность простых чисел;

- последовательность чисел, обратных натуральным.

• Виды последовательностей

• 10, 11, 12, 13,…, 99

• 1, 2, 3,…, 10,….
• 1, 2, 3,…, 10,….
• -1, -2, -3,….

• Конечные
• Бесконечные
• Возрастающие
• Убывающие

Способы задания последовательностей

АНАЛИТИЧЕСКИЙ

АНАЛИТИЧЕСКИЙ

С помощью формулы n-ого члена – позволяет вычислить член последовательности с любым заданным номером

С помощью формулы n-ого члена – позволяет вычислить член последовательности с любым заданным номером

Х n = 3n + 2

РЕККУРЕНТНЫЙ

от слова recursio - возвращаться

х 1 = 1; х n+1 = (n+1)x n

n = 1 ; 2; 3; …

х 2 = (1+1)x 1 = 2·1=2

х 3 = (2+1)x 2 = 3·2=6

х 4 = (3+1)x 3 = 4·6=24

х 5 = (4+1)x 4 = 5·24=120

х 6 = (5+1)x 5 = 6·120=720

х 2 = (1+1)x 1 = 2·1=2

х 3 = (2+1)x 2 = 3·2=6

х 4 = (3+1)x 3 = 4·6=24

х 5 = (4+1)x 4 = 5·24=120

х 2 = (1+1)x 1 = 2·1=2

х 2 = (1+1)x 1 = 2·1=2

х 3 = (2+1)x 2 = 3·2=6

х 4 = (3+1)x 3 = 4·6=24

х 2 = (1+1)x 1 = 2·1=2

х 3 = (2+1)x 2 = 3·2=6

X 5 = 3 . 5 + 2 = 17

Х 45 = 3 . 45 + 2 = 137

X 5 = 3 . 5 + 2 = 17

СЛОВЕСНЫЙ

СЛОВЕСНЫЙ

С помощью описания

С помощью описания

Например: Записать последовательность, все члены которой с нечётными номерами равны -10, а с чётными номерами равны 10.

-10; 10; -10; 10; -10; 10; …

Например: Записать последовательность, все члены которой с нечётными номерами равны -10, а с чётными номерами равны 10.

• 2, 4, 6, 8, 10, . . .
• 5,10,15,20,25, …

Назовите 1,2,3,4,5-ый члены последовательности

a 1 = 2 a 1 = 5

a 2 = 4 a 2 = 10

a 3 = 6 a 3 = 15

a 4 = 8 a 4 = 20

a 5 = 10 a 5 = 25

ЗАДАЧА:

Последовательность задана формулой

a n = 6n – 1 .

Найдите первые пять членов этой последовательности.

Учебник №692 , №694, №696

Последовательность задана формулой 1 в. a n = 7 n – 1

2 в. a n = 3n + 2

Найдите первые пять членов этой последовательности.

ОТВЕТ:

1 В. 6, 13, 20, 27, 34. 2 В. 5, 8, 11, 14, 17.

Проверка самостоятельной работы

1 вариант

2 вариант

• № 1 3, 1, 5/9, 3/8, 7/25, 2/9.
• № 2 2, 6, 10, 14, 18.
• № 3 11, 22, 33,44,55,66,77,88,99 .
• № 4 – 2 числа

• № 1 0, ¼, 2/9, 3/10,4/25
• № 2 1, 4,10, 22,46,94 .
• № 3 18,27,36,45,54,63,72,81,90,99.
• № 4 - бесконечно
• 3, 2,5/3,3/2,7/5, 4/3,9\7. 5/4, 11/9, …

• (2,5/4, 1,7/8, …)

Домашнее задание:

• &21 вопросы 1-9
• № 693
• № 697
• № 699
• № 708 (1)

1) Что называют числовой последовательностью?

2) Как ее можно задать?

3) Какой способ помогает быстрее отыскать любой член последовательности?

Сегодня на уроке

• Я запомнил…

• Я узнал…

• Я научился…

В дальнейшем мне хотелось бы…