Урок алгебры по теме: "Элементы теории вероятностей"

Конспект урока алгебры в 7 классе

в рамках «Региональной Недели теории вероятности»

Тема занятия: Элементы теории вероятностей.

Цель занятия:

познакомить учащихся с основным понятиям теории вероятностей - событием, сформировать умение определять вид произошедшего события. Получить формулу подсчета вероятности.

Оборудование: проектор, презентация Microsoft PowerPoint.

- знакомство с предметом теории вероятностей, местом теории вероятностей в системе научного познания мира.

- формирование у учащихся единой научной картины мира и элементов научного мировоззрения путем исследования метапредметных связей теории вероятностей и различных наук;

- владение интеллектуальными умениями и мыслительными операциями;

Ход занятия

I этап. Разминка.

Подготовимся к уроку. Я вам читаю вопросы, а вы быстро на них отвечаете.

1. Сколько дырок окажется в клеёнке, если во время обеда 12 раз проткнуть её вилкой с 4 зубчиками? (12∙4=48 дырок)

2. Под каким деревом сидит заяц, когда идет дождь? (под мокрым)

3. Сколько концов у двух палок? А у двух с половиной? (4, 6)

4. На столе лежало 4 яблока. Одно из них разрезали пополам и положили на стол. Сколько яблок на столе? (4)

5. Какое число становится больше, если его перевернуть вверх ногами (6 было 9 станет)

II этап. Новый материал.

Запишем в тетрадях число, тему сегодняшнего занятия: «Элементы теории вероятностей».

Ситуация.

Вы забыли вечером собрать портфель в школу. Утром, проснувшись, совершенно сонные, хватаете три первых попавшихся учебника с полки, на которой стоят 10 учебников. В этот день у вас три урока: математика, русский язык, биология. Как думаете, вы взяли все нужные учебники?

Что более вероятно:

-вы взяли все три нужных учебника;

-нужные и ненужные учебники;

-все три ненужных учебника?

(более вероятно, что будут нужные и ненужные учебники, а менее вероятно, что все три нужных).

Точные ответы на такие вопросы дает специальный раздел математики - теория вероятностей.

Выясним, что из себя представляет теория вероятностей.

Предлагаю Опыт:

положим в непрозрачную коробку 12 одинаковых на ощупь картонных карточек: 5 красных и 7 зеленых.

Затем, вынем из коробки одну карточку наугад.

Будем доставать из коробки карточки. Это действие называется экспериментом (или опытом). Вытащенная карточка любого цвета – результат эксперимента, он называется событием. События обозначаются заглавными буквами К, З.

Карточку какого цвета вы вынули?

Кратко обсуждаются полученные результаты.

Часто нам приходится сталкиваться с явлениями, наступление или не наступление которых заранее предвидеть нельзя.

Нельзя заранее точно указать: выпадет герб или цифра при подбрасывании монеты, окажется выигрышным или невыигрышным приобретённый билет лотереи, попадёт или не попадёт пуля в цель при одном выстреле. Такие явления называются случайными.

Случайным называют событие, которое в данных условиях может произойти, а может и не произойти. Очень важным здесь являются УСЛОВИЯ.

Теория вероятностей подобно другим наукам развилась из потребностей практики. Её возникновение относят к середине XVII, а годом становления теории вероятностей как науки считается 1654 год.

Все события бывают: случайными, достоверными и невозможными. Как вы думаете, если из нашей коробки достать синий шар, какое это будет событие? (случайное). Случайное событие – событие, которое в данном опыте может произойти или не произойти.

Достали из коробки черный шар (невозможное). Таких шаров просто нет. Событие, которое не может произойти в данном опыте – невозможное.

Оставим в коробке только желтые шары. Достали из коробки желтый шар (достоверное). В коробке нет шаров другого цвета. Событие, которое обязательно произойдет в данном опыте – достоверное.

Оставим в коробке 1 зеленый и 1 желтый шар. События: достали зеленый шар и достали желтый шар считаются равновозможными, так как нет причины полагать, что одно событие является более возможным, чем другое. Шаров одинаковое количество в коробке.

III этап.

Проведем эксперимент, который поможем нам определить формулу для подсчета вероятности.

Сложим в коробку 5 шаров: 3 красных и 2 желтых. Будем доставать по одному шару. Появление каждого шара из коробки – исход эксперимента. Все исходы будут равновозможными, потому что все шары одинаковые на ощупь, тщательно перемешаны. Значит, имеем 5 равновозможных исходов испытания.

Какова же вероятность того, что из коробки достанем шар красного цвета? Сколько раз в нашем эксперименте мог появиться красный шар? Три раза, так как в коробке 3 шара красного цвета. Значит, красный шар может появиться в трех случаях из всех пяти. Итак, всех возможных исходов эксперимента – 5, благоприятных из них (появление красного шара) – 3. Вероятность появления красного шара в данном эксперименте 3 из 5 или .

Этот пример позволил нам получить формулу подсчета вероятности, которая называется классической формулой

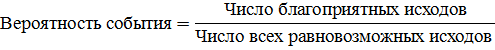
Вероятность достоверного события равна 1. Вероятность невозможного события равна 0. Вероятность любого события больше 0 и меньше 1. Подумайте, почему.

1. В коробке 14 шаров, из которых 2 красных, 3 зеленых, 4 синих, 5 желтых. Из коробки достают 1 шар. Определите, какова вероятность того, что этот шар окажется желтым? Красным? Синим? Зеленым?

IV этап. Подведение итогов

С чем познакомились сегодня на уроке: Проводили эксперимент – в результате событие.

Какие бывают события? (Достоверные, невозможные, случайные)

Как посчитать вероятность события? (Посчитать все равновозможные исходы, все благоприятствующие исходы и разделить вторые на первые).

Домашнее задание

1. Придумайте по три примера событий: достоверных, невозможных, случайных.

2. Подумайте и запишите. В коробке 10 шаров, из них 6 белых, 4 черных. Из коробки достают 1 шар. Определите, какова вероятность того, что этот шар окажется черным? Белым? Красным?