Углы и расстояния в пространстве

Документ содержит несколько геометрических задач с их решениями.

Весь материал - смотрите документ.

Углы и расстояния в пространстве

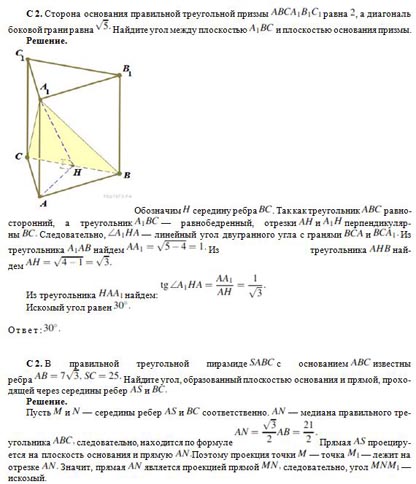
C 2. Сто­ро­на ос­но­ва­ния пра­виль­ной тре­уголь­ной приз­мы  равна , а диа­го­наль бо­ко­вой грани равна  Най­ди­те угол между плос­ко­стью  и плос­ко­стью ос­но­ва­ния приз­мы.

Ре­ше­ние.

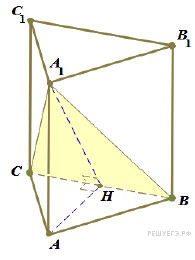Обо­зна­чим  се­ре­ди­ну ребра . Так как тре­уголь­ник  рав­но­сто­рон­ний, а тре­уголь­ник  — рав­но­бед­рен­ный, от­рез­ки  и  пер­пен­ди­ку­ляр­ны  Сле­до­ва­тель­но,  — ли­ней­ный угол дву­гран­но­го угла с гра­ня­ми  и  Из тре­уголь­ни­ка  най­дем  Из тре­уголь­ни­ка  най­дем 

Из тре­уголь­ни­ка  най­дем: 

Ис­ко­мый угол равен 

Ответ:

C 2. В пра­виль­ной тре­уголь­ной пи­ра­ми­де  с ос­но­ва­ни­ем  из­вест­ны ребра  Най­ди­те угол, об­ра­зо­ван­ный плос­ко­стью ос­но­ва­ния и пря­мой, про­хо­дя­щей через се­ре­ди­ны ребер  и 

Ре­ше­ние.

Пусть  и  — се­ре­ди­ны ребер  и  со­от­вет­ствен­но.  — ме­ди­а­на пра­виль­но­го тре­уголь­ни­ка  сле­до­ва­тель­но, на­хо­дит­ся по фор­му­ле  Пря­мая  про­еци­ру­ет­ся на плос­кость ос­но­ва­ния и пря­мую По­это­му про­ек­ция точки  — точка  — лежит на от­рез­ке  Зна­чит, пря­мая  яв­ля­ет­ся про­ек­ци­ей пря­мой  сле­до­ва­тель­но, угол  — ис­ко­мый.

 где  — центр ос­но­ва­ния, зна­чит,  — сред­няя линия тре­уголь­ни­ка  по­это­му . Тогда и  Из пря­мо­уголь­но­го тре­уголь­ни­ка  на­хо­дим:

Из пря­мо­уголь­но­го тре­уголь­ни­ка  на­хо­дим:

Зна­чит, ис­ко­мый угол равен 

Ответ: 

C 2. В пра­виль­ном тет­ра­эд­ре  най­ди­те угол между вы­со­той тет­ра­эд­ра  и ме­ди­а­ной  бо­ко­вой грани .

Ре­ше­ние.

Пусть и  — сред­няя линия тре­уголь­ни­ка . Тогда , зна­чит,  и, сле­до­ва­тель­но, . Кроме того, .

Пусть длина ребра тет­ра­эд­ра равна , тогда имеем:

Ответ: .

C 2. В пра­виль­ной ше­сти­уголь­ной пи­ра­ми­де SABCDEF сто­ро­ны ос­но­ва­ния ко­то­рой равны 1, а бо­ко­вые ребра равны 2, най­ди­те угол между пря­мы­ми SB и CD.

Ре­ше­ние.

Вме­сто пря­мой CD рас­смот­рим па­рал­лель­ную ей пря­мую BE. Ис­ко­мый угол равен углу SBE. Тре­уголь­ник SBE рав­но­сто­рон­ний, по­сколь­ку боль­шая диа­го­наль пра­виль­но­го ше­сти­уголь­ни­ка вдвое боль­ше его сто­ро­ны: . Сле­до­ва­тель­но, .

Ответ: .