Конспект урока
Тема: Перпендикулярные прямые. Перпендикулярность в пространстве.
Цели урока:
Образовательная: повторить, обобщить и систематизировать знания по данной теме; обобщить навыки решения задач по данной теме.
Развивающая: формировать умение анализировать; развитие пространственного воображения.
Воспитательная: формировать у учеников наблюдательность.
Оборудование: таблицы, карточки.
План урока
Организационный момент.
Актуализация опорных теоретических знаний.
Решение основных задач на построение в пространстве.
Задачи для устной работы.
Решение задач.
Задачи для учащихся с высоким уровнем подготовки.
Тестирование.
Итоги урока.
Ход урока
Организационный момент.
Актуализация опорных теоретических знаний.
Перпендикулярные прямые в плоскости. Расстояние между параллельными прямыми. Перпендикулярность прямых в пространстве. Признак перпендикулярности прямой и плоскости. Построение перпендикулярных прямой и плоскости. Свойства перпендикулярных прямой и плоскости. Перпендикуляр и наклонная. Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей. Расстояние между скрещивающимися прямыми.
Примечание. Работа с тематическими таблицами «Перпендикулярные прямые», «Перпендикулярность в пространстве» организуется учителем по усмотрению фронтально или индивидуально. Из учащихся с высокими учебными возможностями можно создать отдельную группу для самостоятельного повторения теории, составления опорной таблицы и решения задач. Эти таблицы могут быть показаны в форме слайд-лекции.
Математический диктант
| Вариант 1
|
| 1. Какое из следующих утверждений неверно? а) если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая прямая перпендикулярна к этой прямой; б) прямая называется параллельной плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости; в) две прямые, перпендикулярные к плоскости, параллельны; г) если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости; д) через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна. 2. Две скрещивающиеся прямые взаимно перпендикулярны. Чему равен угол между ними? а) 90°; б) 0°; в) 180°; г) 45°; д) определить нельзя. 3. Через вершину квадрата ABCD проведена прямая AM, перпендикулярная его плоскости. Какое из следующих утверждений неверно? a) ; ; б) ; ; в) ; ; г) ; ; д) . . 4. Прямая т перпендикулярна к прямым а и b, лежащим в плоскости  , но т не перпендикулярна к плоскости , но т не перпендикулярна к плоскости  . Выясните взаимное расположение прямых а и b: . Выясните взаимное расположение прямых а и b: а) параллельны; б) пересекаются; в) скрещиваются; г) совпадают; д) определить нельзя. 5. Прямая перпендикулярна к двум плоскостям, тогда плоскости: а) пересекаются; б) параллельны; в) определить нельзя; г) скрещиваются; д) совпадают. 6. В тетраэдре 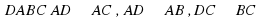 . Тогда прямая ВС и плоскость ADC: . Тогда прямая ВС и плоскость ADC: а) параллельны; б) прямая лежит в плоскости; в) прямая пересекает плоскость, но не перпендикулярна к плоскости; г) прямая перпендикулярна к плоскости, но не пересекает плоскость; д) перпендикулярны. 7. Какое из следующих утверждений неверно? а) Перпендикуляр и наклонная, выходящие из одной точки, имеют разную длину; б) расстояние от точки до плоскости называется длиной перпендикуляра, проведенного из данной точки к данной плоскости; в) равные наклонные, проведенные к плоскости из одной точки, имеют разные проекции; г) проекцией точки на плоскость является точка; д) угол между прямой и плоскостью, пересекающей эту прямую и не перпендикулярной к ней, называется углом между прямой и ее проекцией на эту плоскость. 8. Расстояния от точки М до вершин прямоугольного треугольника 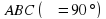 равны. Какое из следующих утверждений верно? равны. Какое из следующих утверждений верно? а) плоскости МАВ и ABC перпендикулярны; б) плоскости МВС и ABC перпендикулярны; в) плоскости MAC и ABC перпендикулярны; г) плоскости MAC и МВС перпендикулярны; д) условия в пунктах а) – г) неверны. 9. Плоскости 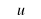 пересекаются по прямой пересекаются по прямой 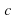 . Плоскость . Плоскость  перпендикулярна плоскости перпендикулярна плоскости  , но не перпендикулярна плоскости , но не перпендикулярна плоскости  . Выясните взаимное расположение прямой с и плоскости . Выясните взаимное расположение прямой с и плоскости  . . а) ; ; б)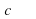 ; ; в) ; ; г) определить нельзя; д) с уверенностью можно сказать только то, что прямая с не перпендикулярна плоскости  . . 10. Какое из следующих утверждений верно? а) двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а; б) двугранный угол имеет бесконечное множество различных линейных углов; в) градусной мерой двугранного угла называется градусная мера его линейного угла; г) угол между пересекающимися плоскостями может быть тупым; д) если одна из двух плоскостей проходит через прямую, пересекающую другую плоскость, то такие плоскости перпендикулярны. |
| Вариант 2 |
| 1. Если угол между двумя прямыми равен 90°, то эти прямые: а) пересекаются; б) параллельны; в) скрещиваются; г) перпендикулярны; д) совпадают. 2. Какое из следующих утверждений неверно? а) Если прямая перпендикулярна к двум прямым, лежащим плоскости, то она перпендикулярна к этой плоскости; б) если прямая перпендикулярна к плоскости, то она ее пересекает; в) если две плоскости перпендикулярны к прямой, то они параллельны; г) если две прямые перпендикулярны к плоскости, то они параллельны; д) если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости. 3. Если одна из двух скрещивающихся прямых перпендикулярна к плоскости, то будет ли перпендикулярна к этой плоскости вторая прямая? а) Да; б) да, но при определенных условиях; в) определить нельзя; г) нет; д) другой ответ. 4. Прямая а перпендикулярна к прямым с и b, лежащим в плоскости , прямая а перпендикулярна к плоскости , прямая а перпендикулярна к плоскости  . Каково взаимное расположение прямых с и b? . Каково взаимное расположение прямых с и b? а) Параллельны; б) пересекаются; в) параллельны или пересекаются; г) совпадают; д) определить нельзя. 5. Одна из двух параллельных плоскостей перпендикулярна к прямой, тогда: а) другая плоскость параллельна прямой; б) прямая лежит в другой плоскости; в) другая плоскость перпендикулярна прямой; г) прямая пересекает другую плоскость; д) выполняются все случаи, указанные в пунктах а) - г). 6. Точка Е не принадлежит плоскости прямоугольника  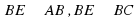 . Тогда прямая CD и плоскость ВСЕ: . Тогда прямая CD и плоскость ВСЕ: а)параллельны; б) перпендикулярны; в) скрещиваются; г) прямая лежит в плоскости; д) перпендикулярны, но не пересекаются. Какое из следующих утверждений неверно? а) Перпендикуляр и наклонная, выходящие из одной точки, имеют равные длины; б) проекцией прямой на плоскости является точка или прямая; в) наклонные разной длины, проведенные к плоскости из одной имеют проекции разных длин; г) прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна к ее проекции; д) расстояние от произвольной точки одной из параллельных плоскостей до другой плоскости называется расстоянием между параллельными плоскостями. 8. Расстояния от точки М до сторон прямоугольного треугольника 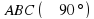 равны. Какое из следующих утверждений верно? равны. Какое из следующих утверждений верно? а) плоскости МАЕ и АБС перпендикулярны; б) плоскости МВС и ABC перпендикулярны; в) плоскости MAC и ABC перпендикулярны; г) плоскости MAC и МВС перпендикулярны; д) условия в пунктах а) - г) неверны. 9. Угол между двумя плоскостями равен 80°. Какое из следующих утверждений неверно? а) плоскости пересекаются; б) в одной из плоскостей найдется прямая, перпендикулярная другой плоскости; в) в одной из плоскостей все прямые не перпендикулярны другой плоскости; г) в одной из плоскостей найдется прямая, параллельная другой плоскости; д) плоскости не перпендикулярны. 10. Какое из следующих утверждений верно? а) градусная мера двугранного угла не превосходит 90°; б) двугранным углом называется плоский угол, образованный прямой 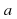 и двумя полуплоскостями с общей границей а; и двумя полуплоскостями с общей границей а; в) если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны; г) угол между плоскостями всегда тупой; д) все линейные углы двугранного угла различны. |
Ответы к математическому диктанту:
| Номер задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Вариант 1 | б | а | г | а | б | д | в | а | д | в |
| Вариант 2 | г | а | г | в | в | б | а | а | б | в |
III. Решение основных задач на построение в пространстве.
Докажите, что через любую точку прямой в пространстве можно провести перпендикулярную ей прямую.
Докажите, что через точку, не лежащую в данной плоскости, нельзя провести более одной прямой, перпендикулярной плоскости.
Докажите, что через данную точку прямой можно провести одну и только одну перпендикулярную ей плоскость.
Докажите, что через данную точку плоскости можно провести одну и только одну перпендикулярную ей прямую.
Докажите, что через любую точку А можно провести прямую, перпендикулярную данной плоскости  .
.
Даны прямая а и плоскость  . Проведите через прямую а плоскость, перпендикулярную плоскости
. Проведите через прямую а плоскость, перпендикулярную плоскости  .
.
IV. Задачи для устной работы.
Работа в группах.
1-я группа.
Дайте определение двугранного угла и его величины.
Проверьте, умеете ли вы строить линейный угол двугранного угла. (См. задания 1-5.)
Задание 1.
Дано: DABC- правильная пирамида.
Построить: линейные углы двугранных углов  .
.
Задание 2.
Дано: SABCD - правильная пирамида.
Построить: линейные углы двугранных углов SADC, SACD, BSCD
Задание 3.
Дано: ABCD - прямоугольник,  .
.
Построить: линейные углы двугранных углов SADB, CSBA, ASDC.
Задание 4.
Дано: BADC - ромб,  .
.
Построить: линейные углы двугранных углов  .
.
Задание 5.
Дано:  - прямоугольный параллелепипед.
- прямоугольный параллелепипед.
Построить: линейные углы двугранных углов  .
.
Какой фигурой является множество всех точек двугранного угла, каждая из которых равноудалена от его граней?
Дана плоскость  и точка А. Сколько можно провести через точку А плоскостей, перпендикулярных плоскости
и точка А. Сколько можно провести через точку А плоскостей, перпендикулярных плоскости  ?
?
Через всякие ли две скрещивающиеся прямые можно про вести перпендикулярные плоскости?
Как расположены грани двугранного угла к плоскости его линейного угла?
Дайте определение угла между пересекающимися плоскостями.
2-я группа.
1. Точка А лежит на ребре двугранного угла. Является ли угол ВАС линейным углом данного двугранного угла, если лучи АВ и АС:
а)перпендикулярны к его ребру;
б) лежат в гранях двугранного угла;
в) перпендикулярны к его ребру, а точки В и С лежат в гранях угла?
Угол АBС - линейный угол двугранного угла с ребром  . Выясните взаимное расположение прямой а и плоскости АBС.
. Выясните взаимное расположение прямой а и плоскости АBС.
Градусная мера одного из двугранных углов, образованных двумя пересекающимися плоскостями, в два раза больше градусной меры другого двугранного угла, образованного теми же плоскостями. Найдите угол между этими плоскостями.
4. Равнобедренные треугольники ABC и DBC с основанием BС не лежат в одной плоскости. Их высоты, проведенные к основанию, равны 5 см, а расстояние между точками А и D также равно 5 см. Найдите меру двугранного угла ABCD.
Прямоугольные равнобедренные треугольники ABC и DBC с прямыми углами в вершине С не лежат в одной плоскости. Их гипотенузы равны 3 см. Расстояние между точками А и D также равно 3 см. Докажите, что плоскости ABC и DBC взаимно перпендикулярны.
Угол между двумя плоскостями равен 80°. Найдется ли в одной из этих плоскостей прямая, перпендикулярная к другой плоскости?
Плоскости  и
и  пересекаются по прямой с. Плоскость
пересекаются по прямой с. Плоскость  перпендикулярна к плоскости
перпендикулярна к плоскости  и не перпендикулярна к плоскости
и не перпендикулярна к плоскости  . Перпендикулярны ли прямая с и плоскость
. Перпендикулярны ли прямая с и плоскость  ?
?
Диагонали основания параллелепипеда равны, а боковое ребро перпендикулярно к основанию. Докажите, что этот параллелепипед прямоугольный.
Три грани параллелепипеда, имеющие общую вершину, являются прямоугольниками. Докажите, что этот параллелепипед прямоугольный.
Диагонали грани параллелепипеда не равны. Является ли этот параллелепипед прямоугольным?
Три измерения прямоугольного параллелепипеда равны 1 м, 2 м и 3 м. Найдите: . По готовому рисунку куба:
. По готовому рисунку куба:
а) докажите, что диагональ куба перпендикулярна любой диагонали грани куба, не пересекающей ее;
б) докажите, что  ;
;
в) расскажите, как можно провести перпендикуляр к плоскости  ;
;
г) что является ортогональной проекцией четырехугольника  на каждую из плоскостей граней куба?
на каждую из плоскостей граней куба?
3-я группа.
Угол между двумя прямыми равен 90°. Как называются такие прямые? (Две скрещивающиеся прямые взаимно перпендикулярны. Чему равен угол между ними?)
Прямые а и т взаимно перпендикулярны, прямая b параллельна прямой а. Чему равен угол между прямыми т и b? (Прямая т не перпендикулярна к прямой а и параллельна прямой b. Могут ли прямые а и b быть взаимно перпендикулярными?)
Одна из двух скрещивающихся прямых перпендикулярна к плоскости. Перпендикулярна ли к этой плоскости вторая прямая? (Плоскость перпендикулярна к одной из скрещивающихся прямых. Перпендикулярна ли эта плоскость ко второй прямой?)
Одна из двух данных прямых перпендикулярна к плоскости, а вторая не пересекает эту плоскость. Могут ли быть параллельными эти прямые? (Плоскость, перпендикулярная к одной из двух данных прямых, не пересекает вторую прямую. Могут ли эти прямые быть параллельными?)
5. Прямая b лежит? в плоскости , прямая а перпендикулярна к любой прямой, лежащей в плоскости
, прямая а перпендикулярна к любой прямой, лежащей в плоскости  , и параллельна прямой b. Перпендикулярны ли прямая а и плоскость
, и параллельна прямой b. Перпендикулярны ли прямая а и плоскость ? (Прямая а лежит в данной плоскости, прямая b перпендикулярна к этой плоскости. Чему равен угол между этими прямыми?)
? (Прямая а лежит в данной плоскости, прямая b перпендикулярна к этой плоскости. Чему равен угол между этими прямыми?)
6. Прямая т перпендикулярна к прямым а и b, лежащим в одной плоскости, и не перпендикулярна к этой плоскости. Выясните взаимное расположение прямых а и b. (Точки А, В, С и D не лежат в одной плоскости. Углы ABC и ACD равны 90°. Найдите угол между прямыми АС и BD.)
4-я группа.
1. Через точку С проведены прямые а и b, пересекающие плоскость  соответственно в точках А и В, причем прямая b перпендикулярна к плоскости
соответственно в точках А и В, причем прямая b перпендикулярна к плоскости  . Как называются отрезки СА, СВ, АВ, точки А и В?
. Как называются отрезки СА, СВ, АВ, точки А и В?
Сторона КМ треугольника КМР перпендикулярна к плоскости  , а сторона MP лежит в этой плоскости. Как можно назвать стороны данного треугольника?
, а сторона MP лежит в этой плоскости. Как можно назвать стороны данного треугольника?
Точки В и С лежат в плоскости  , точка А не лежит в ней. Отрезок АВ меньше отрезка АС. Какой из этих отрезков не может быть перпендикулярным, проведенным из точки A к плоскости
, точка А не лежит в ней. Отрезок АВ меньше отрезка АС. Какой из этих отрезков не может быть перпендикулярным, проведенным из точки A к плоскости  ?
?
Расстояние от точки М до плоскости равно 5 см. Чему равна длина перпендикуляра, проведенного из точки М к этой плоскости?
Точки А и В лежат в плоскости  , а точка D не лежит в этой плоскости. Какой из отрезков DA и DB является наклонной к данной плоскости, если DA = 12 см, DB = 13 см?
, а точка D не лежит в этой плоскости. Какой из отрезков DA и DB является наклонной к данной плоскости, если DA = 12 см, DB = 13 см?
Из точки К к плоскости  проведена наклонная КС, равная 13 дм. Найдите ее проекцию, если расстояние от точки К до плоскости равно 5 дм.
проведена наклонная КС, равная 13 дм. Найдите ее проекцию, если расстояние от точки К до плоскости равно 5 дм.
7. Прямая АС параллельна плоскости  . Расстояние от точки А до плоскости равно 5 см. Чему равно расстояние от точки С до плоскости
. Расстояние от точки А до плоскости равно 5 см. Чему равно расстояние от точки С до плоскости  . Лежит ли на этой прямой точка В, если расстояние от нее до плоскости
. Лежит ли на этой прямой точка В, если расстояние от нее до плоскости  равно 3 см? Чему равно расстояние от прямой АС до плоскости
равно 3 см? Чему равно расстояние от прямой АС до плоскости  ?
?
8. Расстояние между параллельными плоскостями равно 5 см. Отрезок, отсекаемый ими на прямой а, равен 7 см. Перпендикулярна ли данная прямая к этим плоскостям?
9. Расстояние между скрещивающимися прямыми а и b равно 8 см. Чему равно расстояние между прямой b и плоскостью  , проходящей через прямую а параллельно прямой b?
, проходящей через прямую а параллельно прямой b?
Отрезок DB - перпендикуляр к плоскости равнобедренного треугольника ABC, а точка М - середина основания АС. Чему равен угол AMD?
Ребро АС тетраэдра ABCD перпендикулярно к плоскости грани BCD, АН- высота грани ABD. Чему равен угол ВHС?
Расстояние от точки А до плоскости  равно 3 см, а расстояние от точки А до точки М, лежащей в плоскости
равно 3 см, а расстояние от точки А до точки М, лежащей в плоскости  , равно 6 см. Найдите угол между прямой АМ и плоскостью
, равно 6 см. Найдите угол между прямой АМ и плоскостью  .
.
Угол между прямой ВС и плоскостью  равен 40
равен 40 . Найдите угол между прямой ВС и прямой BD, перпендикулярной к плоскости
. Найдите угол между прямой ВС и прямой BD, перпендикулярной к плоскости  .
.
Из одной точки к плоскости проведены перпендикуляр и наклонная. Углы, образованные наклонной с ее проекцией и с перпендикуляром, равны. Найдите угол между наклонной и плоскостью.
V. Решение задач.
Задача 1.
В основании пирамиды PABCD ромб ABCD. Высота ее проходит через точку пересечения его диагоналей и образует с ребром РА угол  , а с ребром РВ угол
, а с ребром РВ угол  . Найдите угол между плоскостями РАВ и ABC.
. Найдите угол между плоскостями РАВ и ABC.
Дополнительные вопросы по задаче:
1) Расскажите, как построить проекцию РО на АРВ.
Назовите угол между высотой пирамиды и плоскостью грани АРВ.
В данную пирамиду вписан конус. Назовите радиус его основания.
Задача 2.
В основании пирамиды треугольник со сторонами 13, 14 и 15. Боковое ребро, противолежащее средней по величине стороне основания, перпендикулярно основанию и образует с боковой гранью, проходящей через эту сторону, угол 45°.
Найдите: а) объем пирамиды; б) расстояние от основания ее высоты до боковой грани, не содержащей этой высоты.
Дополнительные вопросы по задаче:
Назовите не менее четырех пар взаимно перпендикулярных плоскостей.
На примере каких-либо двух взаимно перпендикулярных плоскостей в данной задаче покажите все возможные случаи взаимного расположения двух прямых, одна из которых лежит одной плоскости, а другая - в другой.
3) Чему равна величина двугранного угла ВС?
Задача 3.
В правильной четырехугольной пирамиде расстояние от центра основания до боковой грани равно b, угол между высотой пирамиды и боковой гранью  .
.
Найдите:
а) площадь полной поверхности конуса, вписанного в пирамиду;
б) отношение объема конуса к объему пирамиды.
2) На рисунке к задаче постройте общий перпендикуляр ребра основания пирамиды и образующей конуса, расположенной в противолежащей грани.
Задача 4.
1)В правильной треугольной пирамиде расстояние от центра основания до боковой грани равно b. Угол между высотой пирамиды и боковой гранью  .
.
Найдите:
а) площадь полной поверхности конуса, вписанного в пирамиду;
б) отношение объема пирамиды к объему конуса.
2) На рисунке к задаче постройте общий перпендикуляр бокового ребра и противолежащего ребра основания.
VI. Задачи для учащихся с высоким уровнем подготовки.
Задача 5.
Стороны оснований правильной усеченной шестиугольной пирамиды равны  . Расстояние между двумя параллельными ребрами, лежащими в плоскостях различных оснований и в противолежащих боковых гранях, равно
. Расстояние между двумя параллельными ребрами, лежащими в плоскостях различных оснований и в противолежащих боковых гранях, равно  . Вычислите площадь сечения пирамиды плоскостью, проходящей через указанные ребра.
. Вычислите площадь сечения пирамиды плоскостью, проходящей через указанные ребра.
Решение:
Проведем секущую плоскость через параллельные ребра  /
/
Для построения сечения найдем точки К и L пересечения прямой АВ с продолжениями ребер EF и DC. Так как точки К и  лежат в плоскости боковой грани
лежат в плоскости боковой грани  , прямая К
, прямая К пересекает ребро
пересекает ребро  в некоторой точке М. Прямая
в некоторой точке М. Прямая  лежит в плоскости боковой грани
лежит в плоскости боковой грани  и пересекает ребро
и пересекает ребро  в некоторой точке N.
в некоторой точке N.
Треугольники AKF и BLC - равносторонние со сторонами За. В частности, KF = LC = За.

Вынесем плоскость грани  на рисунке.
на рисунке.
.
Аналогично, .

Вынесем плоскость сечения.
Шестиугольник получается из трапеции  отбрасыванием двух равных треугольников КАМ и LBN. Поскольку KL = 9а;
отбрасыванием двух равных треугольников КАМ и LBN. Поскольку KL = 9а;  , а высота трапеции равна b, площадь трапеции равна 5ab. Точка М делит отрезок
, а высота трапеции равна b, площадь трапеции равна 5ab. Точка М делит отрезок  в отношении 1:3, так что высота треугольника КМА, опущенная из точки М на АК, равна
в отношении 1:3, так что высота треугольника КМА, опущенная из точки М на АК, равна  . Поэтому площадь треугольника АКМ равна
. Поэтому площадь треугольника АКМ равна  .
.
.
Ответ:  .
.
Задача 6.
В основании четырехугольной пирамиды SABCD лежит равнобокая трапеция ABCD, для которой AD ВС, АВ = CD = а, AD = За и ВС = 2а. Ребро SC перпендикулярно к плоскости основания и равно h. Через точку С проведено сечение пирамиды плоскостью, параллельной ребрам АВ и SD. Найдите угол между плоскостью сечения и основанием пирамиды.
ВС, АВ = CD = а, AD = За и ВС = 2а. Ребро SC перпендикулярно к плоскости основания и равно h. Через точку С проведено сечение пирамиды плоскостью, параллельной ребрам АВ и SD. Найдите угол между плоскостью сечения и основанием пирамиды.
Решение
Пусть К - точка пересечения плоскости с ребром AD. Тогда  и СК = а, так как АВСК - параллелограмм. Если L - точка пересечения плоскости с ребром SA, то KL
и СК = а, так как АВСК - параллелограмм. Если L - точка пересечения плоскости с ребром SA, то KL SD. Наконец, эта плоскость обязана пересекать ребро SB в такой точке М, что ML
SD. Наконец, эта плоскость обязана пересекать ребро SB в такой точке М, что ML АВ.
АВ.
Перпендикуляр из точки М на плоскость ABCD попадает на точку N на прямой ВС; опустив перпендикуляр NP точки N на отрезок СК, можем заключить, что двугранный угол между плоскостями CKML и ABCD равен углу MPN.
Из DK = а следует, что  , откуда
, откуда . Значит,
. Значит,
. Аналогично. Угол PCN равен 60°, так что .
Следовательно, /
Ответ: .
VII. Тестирование.
Тест «Перпендикулярные прямые. Перпендикулярность в пространстве»
Вариант 1
1. Дан правильный треугольник ABC со стороной, равной 3.Точка О - центр треугольника, ОМ- перпендикуляр к его плоскости, ОМ = 1. Найдите расстояние отточки М до вершин треугольника.
a)  ;
;
б) определить нельзя;
в) 3;
г) 1;
д) 2.
2. Отрезок АВ, равный 5 см, не имеет общих точек с плоскостью  . Прямые АС и ВД перпендикулярные к этой плоскости, пересекают ее в точках С и D соответственно. Найдите BD, если CD= 3 см,
. Прямые АС и ВД перпендикулярные к этой плоскости, пересекают ее в точках С и D соответственно. Найдите BD, если CD= 3 см,  см,
см,  .
.
а) Определить нельзя;
б) 12см;
в)13см;
г)  см;
см;
д) 1см.
3. Расстояние от некоторой точки до плоскости квадрата равно 4 см, а до каждой из его вершин - 6 см. Найдите диагональ квадрата.
а)  см;
см;
б) 5 см;
в)  см;
см;
г)  см;
см;
д)  см.
см.
4. Отрезок АВ пересекает некоторую плоскость в точке О. Прямые AD и ВС, перпендикулярные к этой плоскости, пересекают ее в точках D и С соответственно. Найдите длину АВ. Если  см, BC
см, BC см,
см,  см.
см.
а) 8 см;
б) определить нельзя;
в) 14 см;
г) 9 см;
д)12см.
5. Из точки М к плоскости  проведены две наклонные, длины которых 18 см и
проведены две наклонные, длины которых 18 см и  см. Их проекции на эту плоскость относятся как 3:4. Найдите расстояние от точки М до плоскости
см. Их проекции на эту плоскость относятся как 3:4. Найдите расстояние от точки М до плоскости  .
.
а)  см;
см;
б) 30 см;
в) 6 см;
г)  см;
см;
д)  см.
см.
6. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 см. Найдите расстояние от точки М до плоскости ABC, если АВ = 6 см.
а)4см;
б)  см;
см;
в) 8 см;
г)6см;
д)2см.
7. Через точку А, удаленную от плоскости  на 4 см, проходит прямая, пересекающая плоскость
на 4 см, проходит прямая, пересекающая плоскость  в точке В. Найдите угол между прямой АВ и плоскостью
в точке В. Найдите угол между прямой АВ и плоскостью  , если длина отрезка АВ равна 6 см.
, если длина отрезка АВ равна 6 см.
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  .
.
Из точки к плоскости проведены две равные наклонные. Величина угла между этими наклонными равна 60°. Величина угла между их проекциями равна 90 . Найдите угол между каждой наклонной и ее проекцией.
. Найдите угол между каждой наклонной и ее проекцией.
а) 90°;
б) 60°;
в) 30°;
г) 45°;
д) определить нельзя.
9. Отрезок, длина которого равна 10 см, пересекает плоскость. Его концы находятся соответственно на расстоянии 3 см и 2 см от плоскости. Найдите угол между данным отрезком и плоскостью.
а) 30°;
6)45°;
в) определить нельзя;
г) 60°;
д) 90°.
10. Из точки А к плоскости  проведены две наклонные, одна длиннее другой на 1 см. Проекции наклонных равны 5 см и 2 см. Найдите расстояние от точки А до плоскости
проведены две наклонные, одна длиннее другой на 1 см. Проекции наклонных равны 5 см и 2 см. Найдите расстояние от точки А до плоскости  .
.
а) 10 см;
б)  см;
см;
в)  см;
см;
г) 5 см;
д)  см.
см.
11. Прямая CD перпендикулярна к плоскости остроугольного треугольника ABC, у которого СК- высота. Найдите расстояние от точки А до плоскости CDK, если  см, a
см, a  .
.
а)  см;
см;
б) 2 см;
в)  см;
см;
г) 1 см;
д)  см.
см.
12.Точка М удалена от плоскости треугольника ABC на расстояние, равное 12, и находится на одинаковом расстоянии от его вершин. Найдите угол между прямой МА и плоскостью ABC, если АС = СВ = 8,  .
.
a) arccos ;
;
б) arcsin ;
;
в) arctg ;
;
г) arcctg ;
;
д) arcsin .
.
13. В основании тетраэдра КМРН лежит треугольник МНР с углом H, равным 90°. Прямая НК перпендикулярна к плоскости основания. Найдите расстояние от точки К до прямой MP, если КН= 9 см, PH = 24 см,  .
.
а) 9 см;
б) 12 см;
в) 15 см;
г) 18 см;
д)24см.
14. При пересечении двух плоскостей образовались двугранные углы, один из которых в два раза больше другого. Найдите градусную меру угла между этими плоскостями.
а) 30°;
б)60°;
в) 90°;
г) 120°;
д) 150°.
| Задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Ответы | д | в | д | г | а | д | б |
| Задания | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Ответы | г | а | д | г | в | в | б |
VIII. Итоги урока.
Домашнее задание: повторить
Понятия, не требующие доказательства:
Двугранный угол. Линейный угол двугранного угла. Примеры двугранных углов и их линейных углов в правильной пирамиде.
Параллелепипед. Виды параллелепипеда. Соотношение между числом ребер, числом вершин и числом граней параллелепипеда. Формулы для вычисления объема прямоугольного параллелепипеда и объема наклонного параллелепипеда.
Призма. Виды призм. Соотношение между числом ребер, числом вершин и числом граней призмы. Формулы для вычисления объема прямой призмы и объема наклонной призмы.
4. Прямая призма. Площадь поверхности прямой призмы.
Правильная призма. Площадь полной поверхности правильной призмы.
Объясните, как вычислить площадь боковой поверхности наклонной призмы.
Выпуклый многогранник. Соотношение между числом ребер, числом вершин и числом граней выпуклого многогранника. Правильный многогранник. Виды правильных многогранников. Примеры правильных многогранников с треугольными гранями.
Пирамиды. Виды пирамид. Соотношение между числом ребер, числом вершин и числом граней пирамиды. Формула для вычисления объема пирамиды.
Пирамида. Правильная пирамида. Площадь полной поверхности правильной пирамиды.
Усеченная пирамида. Правильная усеченная пирамида. Площадь полной поверхности усеченной пирамиды.
Понятия, требующие доказательства:
Параллелепипед. Теорема о свойстве противоположных граней параллелепипеда.
Прямоугольный параллелепипед. Теорема о вычислении длины диагонали прямоугольного параллелепипеда.
Параллелепипед. Диагонали параллелепипеда. Теорема, выражающая свойства диагоналей параллелепипеда.
Теорема о вычислении площади боковой поверхности прямой призмы. Площадь полной поверхности прямой призмы.
Правильная призма. Теорема о вычислении площади боковой поверхности правильной призмы.
Пирамида. Теорема о вычислении площади боковой поверхности правильной пирамиды.
Усеченная пирамида. Правильная усеченная пирамида. Теорема о вычислении площади боковой поверхности правильной усеченной пирамиды.
На следующем уроке можно эти вопросы использовать для индивидуальных заданий.
Литература:
Атанасян, Л.С. Геометрия. 7-9 классы: учеб. для общеобразовательных учреждений/Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др. – 19-е изд. – М. : Просвещение, 2009 – 384 с.: ил.
Атанасян, Л.С. Геометрия. 10-11 классы: учеб. для общеобразовательных учреждений: базовый и профильный уровни/Л.С. Атанасян, В.Ф. Бутузов, С.В. Кадомцев и др. – 18-е изд. – М. : Просвещение, 2009 – 255 с. : ил.
Беденко, Н.К. Уроки геометрии на втором курсе средних профтехучилищ: Методическое пособие для средних проф.-тех. училищ. – М.: Высш. шк., 1988 – 96 с.: ил.
Далингер, В.Ф. Методика реализации внутрипредметных связей при обучении математике: Кн. для учителя/В.Ф. Далингер. – М.: Просвещение, 1991 – 80 с.: ил.
Ершова, А.П. устные проверочные и зачетные работы по геометрии для 10-11 класса. – М.: Илекса, - 2005, - 112 с.
Крутова, И.А. Математика в таблицах и схемах. Для школьников и абитуриентов/Крутова И.А. – «Полиграфуслуги», 2006. – 224 с.
Лысенко, Ф.Ф. Математика. Подготовка к ЕГЭ-2010/Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов-на-Дону: Легион-М., 2009. – 480 с.
Лященко, Е.И. Лабораторные и практические работы по методике преподавания математики: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов/Е.И. Лященко, К.В. Зобкова, Т.Ф. Кириченко и др.; Под ред. Е.И. Лященко. – Ь.: Просвещение, 1988. – 223 с.: ил.
66

 Получите свидетельство
Получите свидетельство Вход
Вход


 ;
; ;
; ;
; ;
; .
. , но т не перпендикулярна к плоскости
, но т не перпендикулярна к плоскости 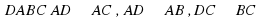 . Тогда прямая ВС и плоскость ADC:
. Тогда прямая ВС и плоскость ADC: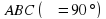 равны. Какое из следующих утверждений верно?
равны. Какое из следующих утверждений верно?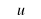 пересекаются по прямой
пересекаются по прямой 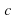 . Плоскость
. Плоскость  перпендикулярна плоскости
перпендикулярна плоскости  ;
;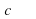 ;
;
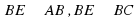 . Тогда прямая CD и плоскость ВСЕ:
. Тогда прямая CD и плоскость ВСЕ: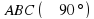 равны. Какое из следующих утверждений верно?
равны. Какое из следующих утверждений верно?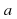 и двумя полуплоскостями с общей границей а;
и двумя полуплоскостями с общей границей а;








 Перпендикулярные прямые. Перпендикулярность в пространстве (86.4 КB)
Перпендикулярные прямые. Перпендикулярность в пространстве (86.4 КB)
 0
0 2658
2658 302
302 Нравится
0
Нравится
0





