Учебный элемент
Тема: «Определенный интеграл»
- 5
Цели:
Изучив данный учебный элемент, Вы узнаете:
Понятие определенного интеграла.
Физический смысл определенного интеграла.
Формулу Ньютона-Лейбница.
Оборудование, материалы и вспомогательные средства:
персональный компьютер;
мультимедиа проектор;
презентация урока;
Сопутствующие учебные элементы и пособия:
1.Учебник «А.Г. Мордкович «Алгебра и начала анализа 10-11 классы»
2.Задачник «А.Г. Мордкович «Алгебра и начала анализа 10-11 классы»
Задача , приводящая к понятию определенного интеграла.(перемещение точки)
По прямой движется материальная точка. Зависимость скорости от времени выражается формулой v=v(t). Найти перемещение точки за промежуток времени [a;b].
Решение. Если бы движение было равномерным, то задача решалась бы очень просто:s=vt , т.е. s=(b-a).
1)Разделим промежуток времени [a;b] на п равных частей.
2)Рассмотрим промежуток времени 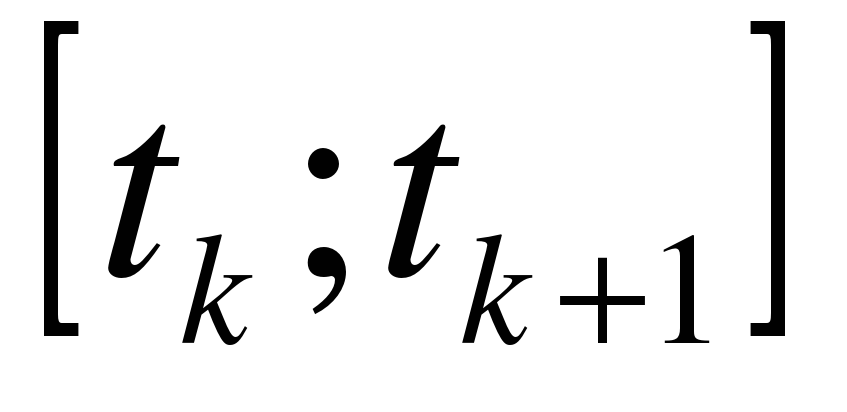 и будем считать, что в этот промежуток времени скорость была постоянной, такой, как в момент времени
и будем считать, что в этот промежуток времени скорость была постоянной, такой, как в момент времени 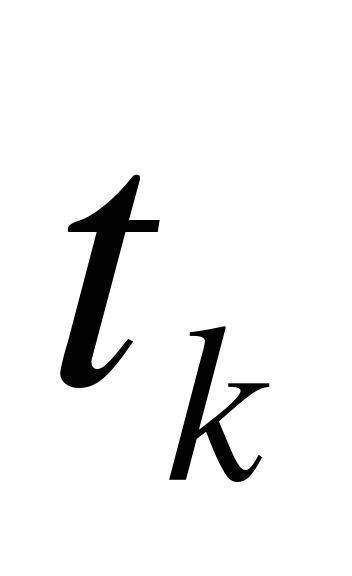 :v=v(
:v=v(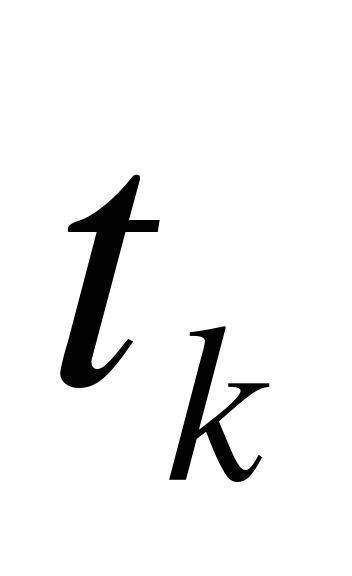 ).
).
3)Найдем приближенное значение перемещения точки за промежуток времени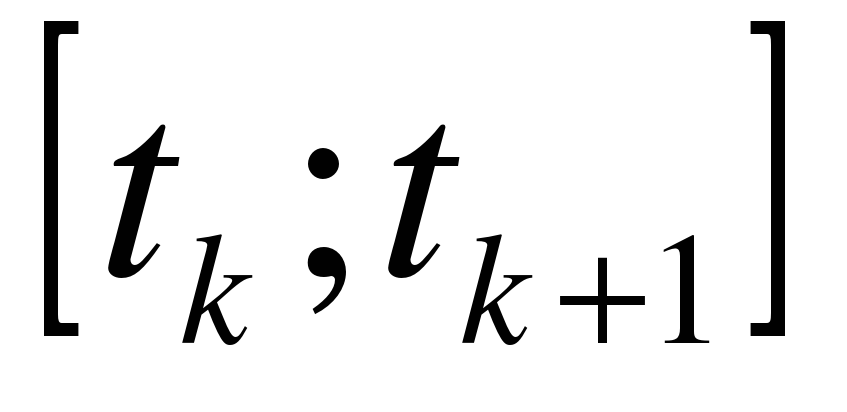 (это приближенное значение обозначим
(это приближенное значение обозначим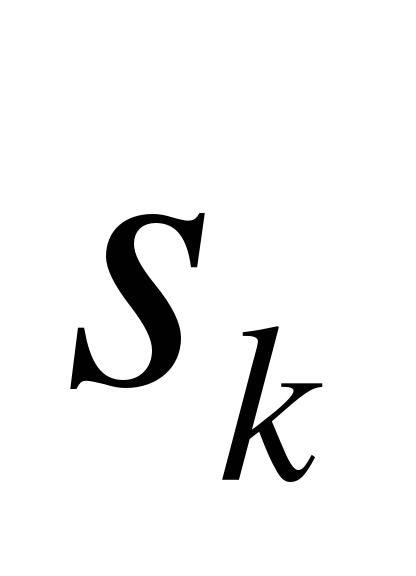 ):
):
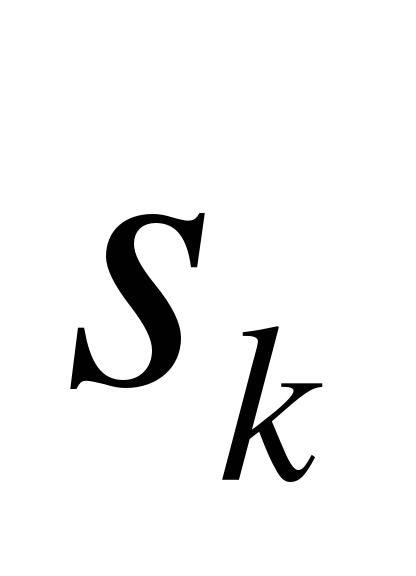 =v(
=v(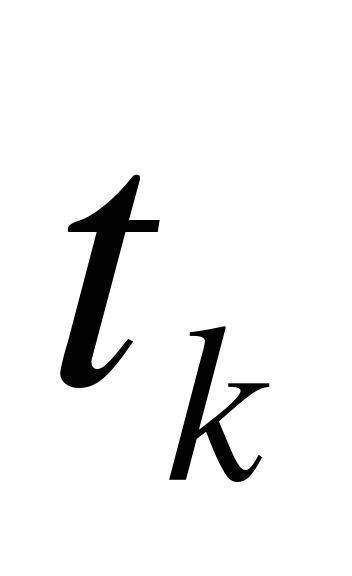 )Δ
)Δ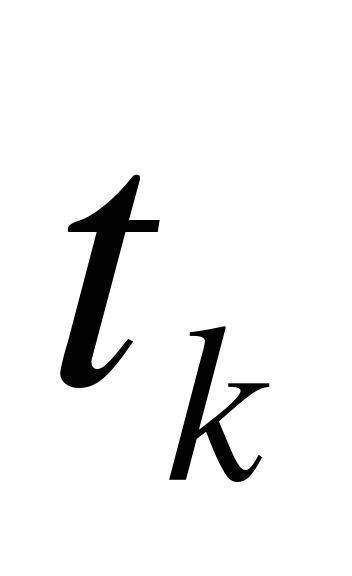
4)Найдем приближенное значение перемещения s:
 ≈
≈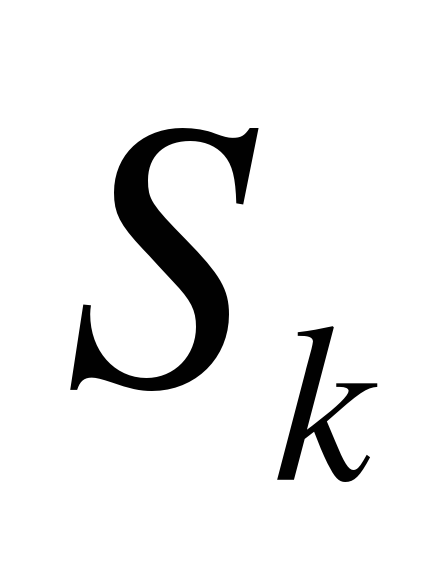 ,где
,где 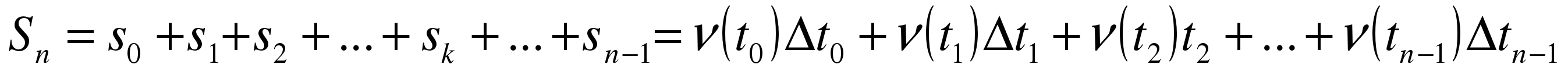
5)Точное значение перемещения вычисляется по формуле
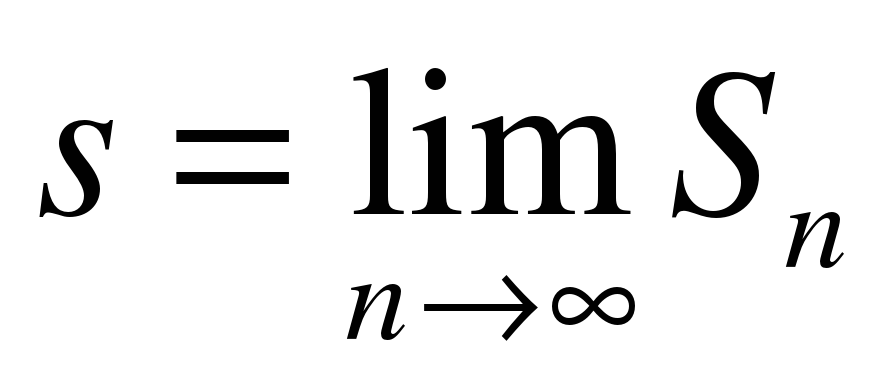
Запись в тетрадь:
Дадим математическое описание модели, для функции y=f(x), непрерывной (но необязательно неотрицательной, как это предполагалось в рассмотренных задачах) на отрезке [a;b]:
разбивают отрезок[a;b] на п равных частей;
составляют сумму
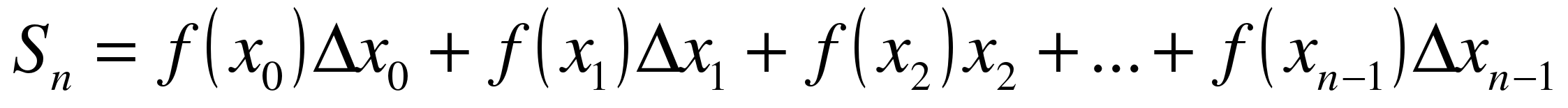
3) вычисляют 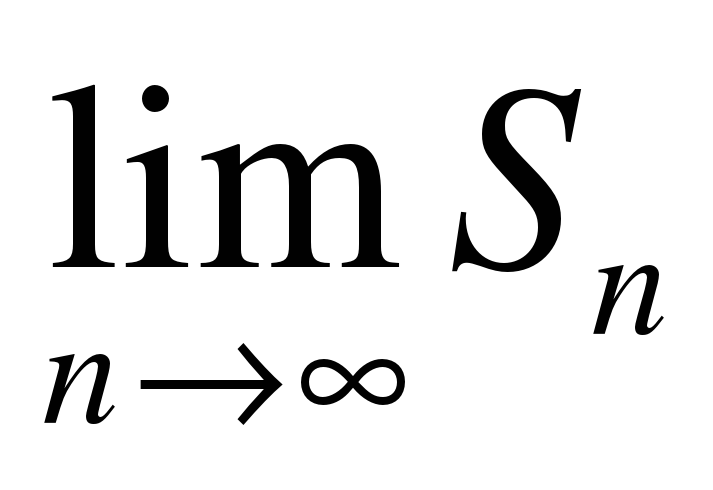 .
.
В курсе математического анализа доказано, что этот предел существует. Его называют определенным интегралом от функции y=f(x), по отрезку [a;b] и обозначают так:
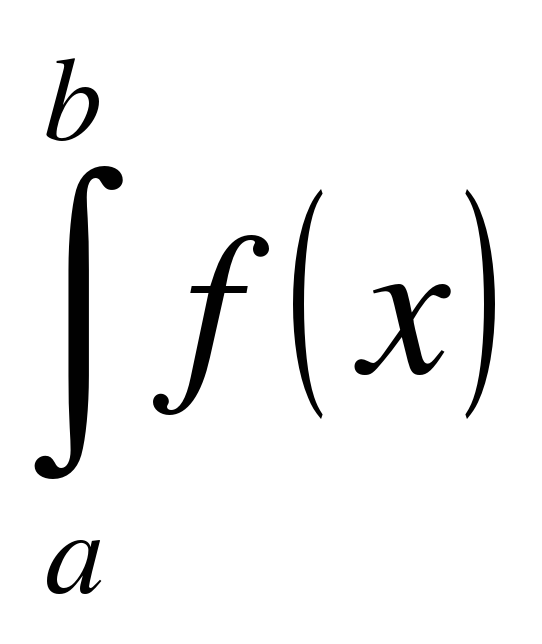
(читают: интеграл от а до в эф от икс дэ икс). Числа а и в называют пределами интегрирования (соответственно нижним и верхним).
Из решения задачи приведенной выше, следует, что перемещение s точки , движущейся по прямой со скоростью v=v(t) , за промежуток времени от t = а до t =b, вычисляется по формуле
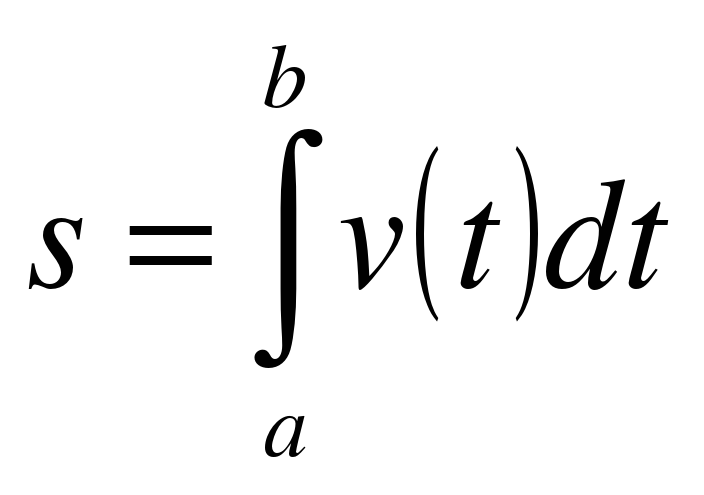
Это физическое истолкование определенного интеграла.
Есть ли какая-либо связь между определенным интегралом и первообразной?
Ключ к разгадке дает задача , приведенная выше, с одной стороны, перемещение s точки, движущейся по прямой со скоростью v=v(t) за промежуток времени от t = а до t = b вычисляется по формуле
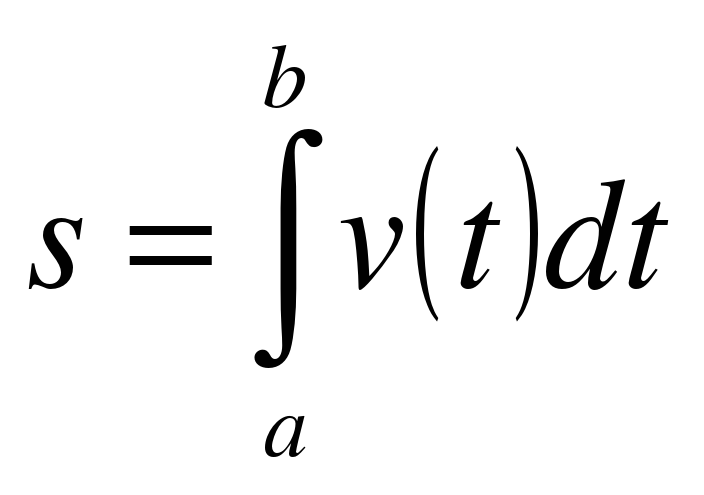
С другой стороны, координата движущейся точки есть первообразная для скорости — обозначим ее s(t); значит, перемещение s выражается формулой s = s(b) — s(а). В итоге получаем
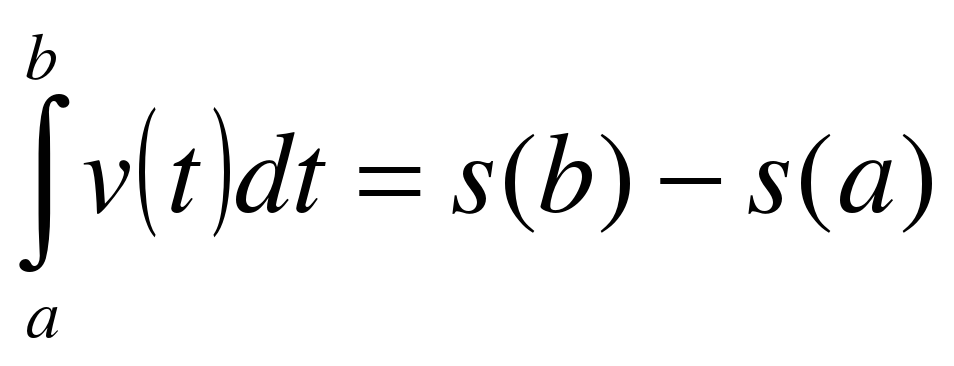
где s(t) — первообразная для v(t).
Запись в тетрадь:
Теорема. Если функция у = f(x) непрерывна на отрезке[a;b] , то справедлива формула
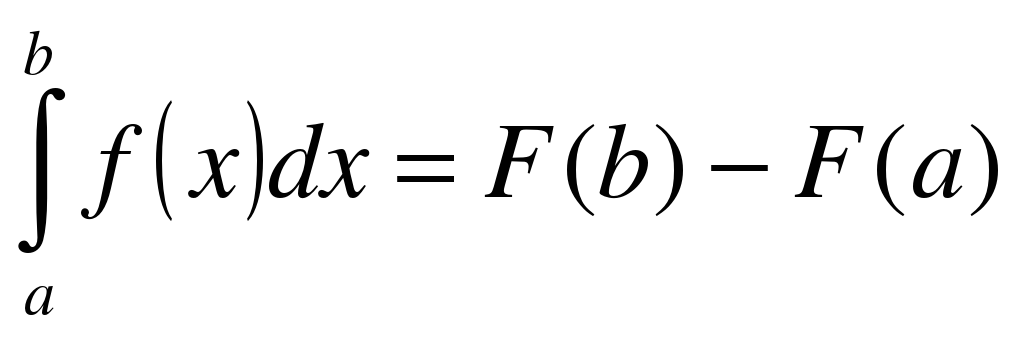 ,
,
где F(х) - первообразная для f(x).
Приведенную формулу обычно называют формулой Ньютона—Лейбница в честь английского физика Исаака Ньютона (1643—1727) и немецкого философа Готфрида Лейбница (1646— 1716), получивших ее независимо друг от друга и практически одновременно.
Замечание. То, что математическую формулу вывели философ и физик, никого не удивляет, ведь математика — язык, на котором говорит сама природа.
На практике вместо записи F(b) - F(а) используют запись
b
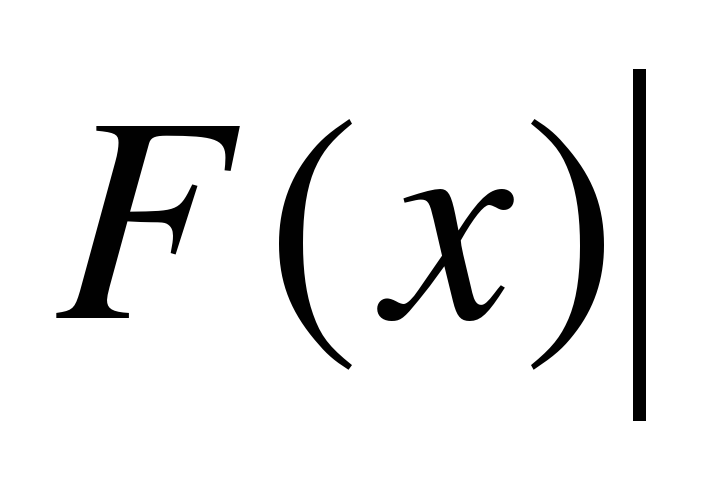
a
(ее называют иногда двойной подстановкой) и соответственно переписывают формулу Ньютона—Лейбница в виде
а
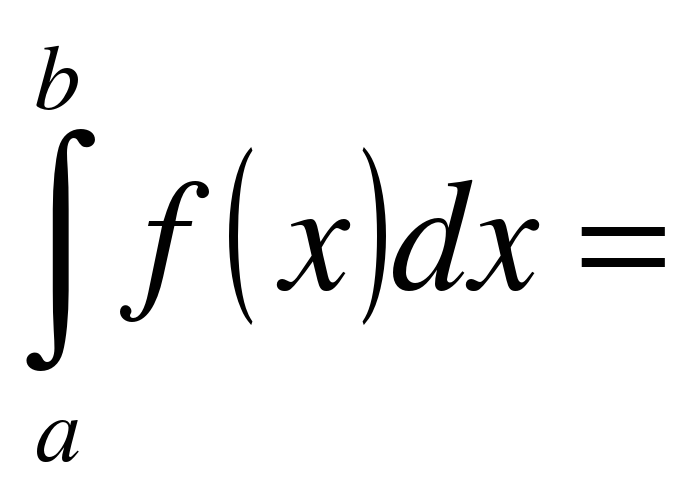
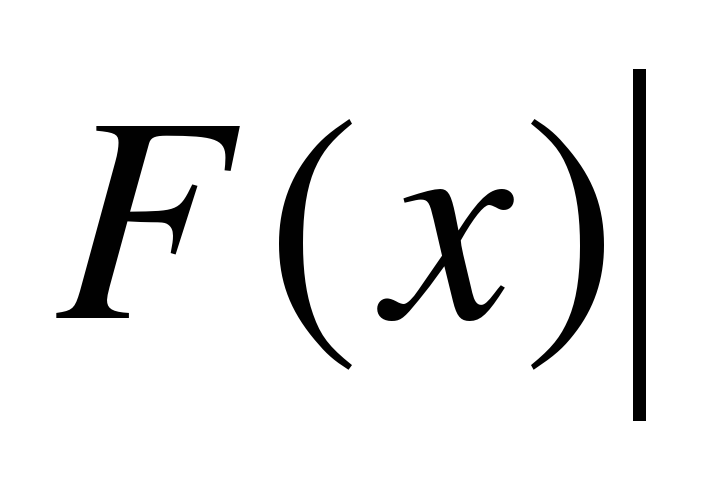
b
Вычисляя определенный интеграл, сначала находят первообразную, а затем осуществляют двойную подстановку.
Пример 1. Вычислить 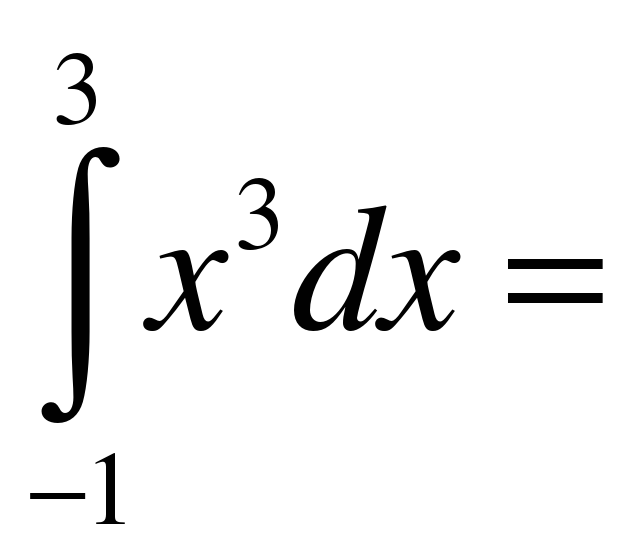
Решение. Первообразной для x3 служит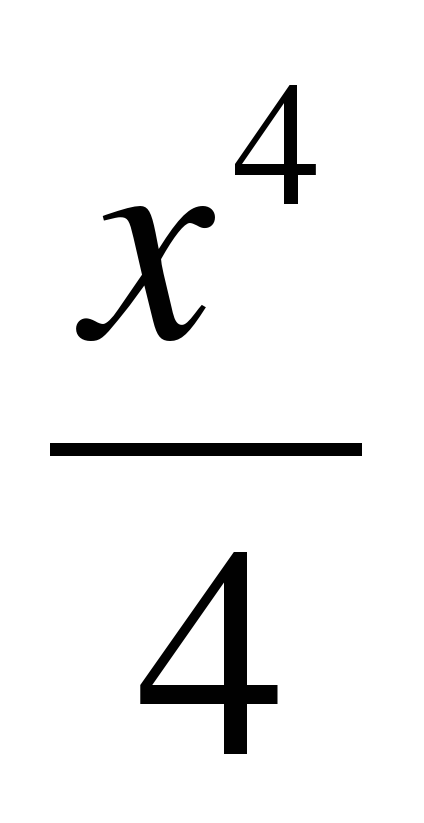 . Значит,
. Значит,
3
-1
Запись в тетрадь:
Решите примеры: №49.1, №49.2(а,б), (если возникнуть трудности при решении обратитесь к преподавателю).
Пример 2. Вычислите площадь фигуры, ограниченной одной полуволной синусоиды y=sinx и осью абцисс.
Решение: Можно взять полуволну синусоиды от точки х=0 до точки х=π и воспользоваться формулой
 при следующих условиях:а=0, в= π, f(x)=sinx. Получим
при следующих условиях:а=0, в= π, f(x)=sinx. Получим


y=sinx





π
0
Запись в тетрадь:
Решите примеры: стр.167 №49.14, №49.15, (если возникнуть трудности при решении обратитесь к преподавателю).
Проверь себя!!!
Домашнее задание:
Липецкий политехнический техникум
Клещина Н.В.


 Получите свидетельство
Получите свидетельство Вход
Вход


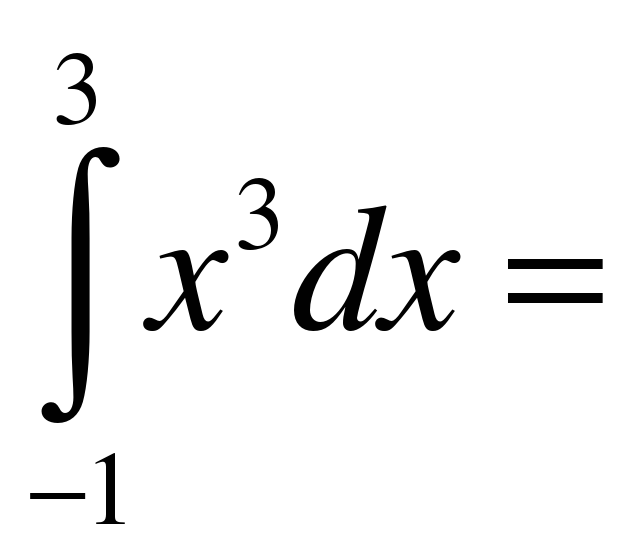









 Учебный элемент по математике "Определенный интеграл" (0.29 MB)
Учебный элемент по математике "Определенный интеграл" (0.29 MB)
 0
0 492
492 9
9 Нравится
0
Нравится
0



