Работу выполнила:
Гончарова Ирина Владимировна,
ученица 7-А класса «Муниципального бюджетного общеобразовательного учреждения Щебетовская
общеобразовательная школа им.М.А.Македонского »
Руководитель:
Гордиёнок Татьяна Викторовна, учитель математики «Муниципального бюджетного общеобразовательного учреждения Щебетовская
общеобразовательная школа им.М.А.Македонского »
г. Феодосия – 2017
СОДЕРЖАНИЕ
Введение …………………………………………………3
2. Жорж Луи Бюффон ……………………………………… 4
3. Опыт Бюффона с иглой …………………………………………5
4. Эксперимент ……………………………………… 7
5. Заключение…………………………………………………9
6. Литература ………………………………………………10
ВВЕДЕНИЕ
История науки показывает, что все ее отрасли по мере своего развития приходят к необходимости учитывать случайные отклонения от закономерностей и использовать их влияние на течение изучаемых процессов. Случайность в окружающем нас мире существует объективно, вследствие принципиальной невозможности учесть все причинные связи изучаемых явлений с бесчисленным множеством других явлений. При развитии науки границы между случайностью и закономерностью изменяются по мере расширения человеческих познаний : то, что являлось случайностью на одном этапе науки, может стать закономерностью на другом ее этапе и, наоборот, в явлениях, которые считались строго закономерными, вследствие совершенствования теории и техники эксперимента, повышения точности определения закономерностей обнаруживаются случайные отклонения от них и возникает необходимость учитывать эти случайные отклонения.
Задача Бюффона об игле была сформулирована в 1733 году, а опубликована вместе с решением только в 1777. Это классическая задача теории геометрических вероятностей, по праву считающаяся исходным пунктом развития этой теории. Появление геометрических вероятностей стало выдающимся событием в науке. Оно способствовало формированию нового языка, стиля и облика теории вероятностей. Благодаря геометрическим вероятностям возникла и бурно развивается интегральная геометрия. Классические результаты Бюффона лежат в основе современного и весьма универсального метода статистического моделирования. В последние годы геометрические вероятности успешно применяются в конечно-элементном анализе.
Жорж Луи Бюффон (1707–1788) —
французский натуралист, биолог, математик,
естествоиспытатель и писатель

Родился 7 сентября 1707 г. в Монбаре (Бургундия). Отец, Бенжамен Леклер, бывший советник парламента в Дижоне, дал сыну блестящее воспитание. В юности Бюффон вместе с молодым герцогом Кингстоном путешествовал по Франции и Италии. Потом отправился в Англию, где перевёл «Теорию флукций» И. Ньютона.
Он выступал и с собственными статьями математического содержания. В 1733 г. Бюффона избрали членом Королевской Академии естественных наук. В 1739 г. учёный был назначен интендантом королевского ботанического сада. Наиболее заметным трудом натуралиста стала многотомная «Естественная история животных» (1749—1783 гг.), где помимо описаний млекопитающих, птиц, рыб (большей частью систематизированных по литературным источникам) приведены гипотезы, касающиеся происхождения Земли, рассуждения по антропологии и т. д. Этот фундаментальный труд, имеющий сейчас в основном историческую ценность, был в своё время довольно популярен в научном мире и переведён почти на все европейские языки.
Бюффон умер 16 апреля 1788 г. в Париже.
До конца жизни он пользовался благосклонностью монархов — французский король Людовик XV возвёл учёного в графское достоинство, а Людовик XVI ещё при жизни Бюффона почтил его бюстом, который был поставлен у входа в королевский естественноисторический кабинет.
Рассмотрим известный опыт Бюффона с иглой по определению числа «пи».
На разграфлённый параллельными равноотстоящими прямыми лист бумаги бросается игла. Если длина иглы меньше расстояния между линейками a, то вероятность события «Игла пересечёт линейку» будет равна 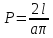 -формула Бюффона (доказательство этой формулы можно найти, например, в книге: Лютикас В.С. Факультативный курс по математике. Теория вероятностей. – М.: Просвещение, 1990.). Проводя такой опыт многократно и заменяя вероятность частотой, можно получить приближённое значение числа «пи».
-формула Бюффона (доказательство этой формулы можно найти, например, в книге: Лютикас В.С. Факультативный курс по математике. Теория вероятностей. – М.: Просвещение, 1990.). Проводя такой опыт многократно и заменяя вероятность частотой, можно получить приближённое значение числа «пи». 
По своей простоте этот опыт доступен каждому. Стоит бросить иглу несколько сотен раз, чтобы получить для π довольно близкое значение. Заметим, что плоскость с нанесёнными на ней параллелями должна быть горизонтальна и падению иглы надо придать случайный характер, для чего бросать её вверх нужно так, чтобы она падала почти вертикально на один из своих концов.
Немецкий профессор Рудольф Вольф произвёл опытную проверку формулы
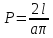 в задаче Бюффона. В опытах Вольфа ширина между параллельными прямыми была a = 45 мм, длина бросаемой иглы l =36мм. Вероятность пересечения иглой параллельных прямых по формуле Бюффона в этом случае будет
в задаче Бюффона. В опытах Вольфа ширина между параллельными прямыми была a = 45 мм, длина бросаемой иглы l =36мм. Вероятность пересечения иглой параллельных прямых по формуле Бюффона в этом случае будет
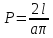 =
= 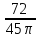 ≈0,5093
≈0,5093
Игла была брошена 5000 раз, причём пересекла параллели 2532 раза. Таким образом, частота события оказалась равной
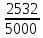 ≈0,5064
≈0,5064
что довольно близко к вероятности 0,5093, вычисленной по формуле.
Результатом опыта Вольфа можно было бы воспользоваться для приближённого вычисления числа π. Допустив на основании теоремы Бернулли (По мере увеличения числа опытов относительная частота события приближается к его вероятности) приближённое равенство 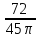 =
=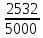
находим для π величину: 3,1595…, которая отличается от истинной менее чем на 0,02.
Впоследствии такие опыты были повторены несколько раз и привели к следующим результатам:
M. A. Smith (1855 г.) — 3204 бросаний — π≈3,1553;
Fox (1894 г.) — 1120 бросаний — π≈3,1419;
Lazzarini (1901 г.) — 3408 бросаний — π≈3,1415929.
Для вычисления числа π этим замечательным по оригинальности способом формулу Бюффона
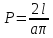
можно упростить, если расстояние a между параллельными прямыми взять в два раза больше длины иглы l: a =2l. Тогда 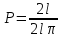 или Р=
или Р=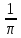
откуда π=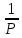
Если игла брошена n раз и пересечение произошло m раз, то, допуская по теореме Бернулли приближённое равенство между вероятностью Р и частотой 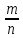 :
:
P≈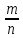
и подставив значение Р в равенство π=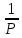 , получим π≈
, получим π≈ 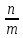
Таким образом, приближённое число π найдётся, если число n всех бросаний иглы разделить на число m случаев, когда игла пересекла параллельные прямые.
ЭКСПЕРИМЕНТ
В следующей сводной таблице приведены известные в настоящее время результаты экспериментов при решении задачи Бюффона об игле.
|
| Относительная длина иглы (l/а) | Число бросков (n) | Число пересечений (m) | Оценка () | Относительная погрешность оценки |
| Вольф 1850 | 0,8 | 5000 | 2532 | 3,1596 | 0,5732 |
| Смит 1855 | 0,6 | 3204 | 1218 | 3,1553 | 0,4363 |
| Де Морган 1860 | 1,0 | 600 | 382 | 3,137 | 0,1462 |
| Фокс 1884 | 0,75 | 1030 | 489 | 3,1595 | 0,5700 |
| Лаззерини 1901 | 0,83 | 3408 | 1808 | 3,1415929 | 0,00001 |
| Рейнс 1925 | 0,5419 | 2520 | 859 | 3,1795 | 1,2067 |
| Гриджеман 1960 | 0,7857 | 2 | 1 | 3,143 | 0,0448 |
Эксперимент в классе
| № серии | n | m | π |
| 1. | 100 | 32 | 3,125 |
| 2 | 100 | 31 | 3,225 |
| 3 | 100 | 32 | 3,125 |
| 4 | 100 | 31 | 3,225 |
| 5 | 100 | 27 | 3,703 |
| 6 | 100 | 33 | 3,030 |
| 7 | 100 | 31 | 3,225 |
| 8 | 100 | 35 | 2,857 |
| 9 | 100 | 32 | 3,125 |
| 10 | 100 | 30 | 3,333 |
| 11 | 100 | 38 | 2,631 |
| 12 | 100 | 34 | 2,941 |
| 13 | 100 | 29 | 3,448 |
| 14 | 100 | 33 | 3,030 |
| 15 | 100 | 30 | 3,333 |
| 16 | 100 | 35 | 2,857 |
| 17 | 100 | 32 | 3,125 |
|
| 1700 | 535 | π≈3,1775 |
ЗАКЛЮЧЕНИЕ
По своей простоте этот опыт доступен каждому. Стоит бросить иглу несколько сотен раз, чтобы получить для π довольно близкое значение. Заметим, что плоскость с нанесёнными на ней параллелями должна быть горизонтальна и падению иглы надо придать случайный характер, для чего бросать её вверх нужно так, чтобы она падала почти вертикально на один из своих концов.
Сейчас, конечно, никто иголку не бросает, а число π вычислено уже далеко за 10 триллионов знаков. Забавно, что такая точность и близко не нужна для практических вычислений — по оценкам, достаточно знать π примерно до 40-го знака после запятой, чтобы точно рассчитать объём видимой Вселенной с точностью до одного атома. Так что вычисление π с такой точностью — это, скорее, гонка за рекордами и соревнование суперкомпьютеров.
ЛИТЕРАТУРА
Лютикас В.С. Факультативный курс по математике. Теория вероятностей. – М.: Просвещение, 1990.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Творческая работа по математике "Иголка Бюффона" (633.98 KB)
Творческая работа по математике "Иголка Бюффона" (633.98 KB)
 0
0 814
814 12
12 Нравится
0
Нравится
0


